НОУ ИНТУИТ | Алгебра матриц и линейные пространства. Лекция 7: Единственность главного ступенчатого вида матрицы

Учитесь и получайте официальные документы БЕСПЛАТНО. Вы можете поддержать наш проект.

Твой путь к знаниям!

Московский государственный университет имени М.В.Ломоносова

Опубликован: 10.09.2007 | Доступ: свободный | Студентов: 3989 / 729 | Оценка: 4.33 / 3.93 | Длительность: 13:22:00

Тема: Математика

Специальности: Математик

Теги: beta, TE, алгебраическим дополнением, вычисления, геометрия, законы дистрибутивности, игры, линейная оболочка строк, матрица перехода, моноид, определитель матрицы, расширенная матрица, система линейных уравнений определенная, собственный вектор, теория, элементы

|

Вам нравится? Нравится 63 студентам

| Поделиться |

Поддержать курс

| Скачать электронную книгу

Аннотация: В данной лекции речь идет о единственности главного ступенчатого вида матрицы. Приведены примеры ступенчатых матриц, рассмотрено понятие изоморфизма линейных пространств, доказана обратимость матрицы перехода. Также приведены доказательства основных теорем и предоставлены задачи для самостоятельного решения

Ключевые слова: линейная оболочка строк, доказательство, определение, матрица, отношение, изоморфизм, базис, пространство, запись, матрица перехода, умножение, поле, равенство, координаты, алгоритм

Единственность главного ступенчатого вида матрицы

Теорема 9.5.1. Пусть 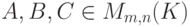$A,B,C\in M_{m,n}(K)$ , B и C - ступенчатые матрицы, полученные из ненулевой матрицы A конечным числом элементарных преобразований строк 1-го, 2-го и 3-го типов. Тогда:

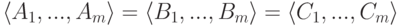
системы строк {B₁,...,B_m} матрицы B и {C₁,...,C_m} матрицы C в линейном пространстве строк Kⁿ линейно выражаются друг через друга (другими словами, линейные оболочки строк матриц A, B и C в K^n совпадают: $\langle A_1,...,A_m\rangle = \langle B_1,...,B_m\rangle = \langle C_1,...,C_m\rangle$
числа r₁ и r₂ ненулевых строк в ступенчатых матрицах B и C соответственно совпадают (при этом $r=r_1=r_2=\dim_K \langle A_1,...,A_m\rangle$ ; другие интерпретации числа r=r(A) будут даны в теореме 9.16.1 о ранге матрицы);
лидеры строк ступенчатых матриц B и C располагаются в одних и тех же столбцах;
если B и C - главные ступенчатые виды ненулевой матрицы $A \in M_{m,n}(K)$ , то B=C.

Доказательство.

В силу замечания 9.4.5, в линейном пространстве строк Kⁿ системы строк {A₁,...,A_m} матрицы A и {B₁,...,B_m} матрицы B линейно выражаются друг через друга. Аналогично, системы строк {A₁,...,A_m} матрицы A и {C₁,...,C_m} матрицы C также линейно выражаются друг через друга. Принимая во внимание транзитивность линейной выражаемости систем строк (см. следствие 9.4.2), получаем, что системы строк {B₁,...,B_m} матрицы B и {C₁,...,C_m} матрицы C линейно выражаются друг через друга. Следовательно,
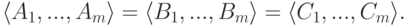
$\langle A_1,...,A_m\rangle = \langle B_1,...,B_m\rangle = \langle C_1,...,C_m\rangle.$
Так как ненулевые строки ступенчатой матрицы образуют максимально независимую подсистему строк, то из 1) следует, что r₁=r₂ (см. следствие 9.4.10), при этом
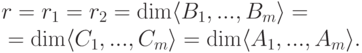
$\begin{mult} r=r_1=r_2=\dim \langle B_1,...,B_m\rangle={} \\* {}= \dim \langle C_1,...,C_m\rangle=\dim \langle A_1,...,A_m\rangle. \end{mult}$
Пусть лидеры r ненулевых строк B₁,B₂,...,B_r ступенчатой матрицы B расположены в столбцах с номерами k₁,k₂,...,k_r, k₁<k₂<...<k_r, а лидеры r ненулевых строк C₁,C₂,...,C_r ступенчатой матрицы C расположены в столбцах с номерами l₁,l₂,...,l_r, l₁<l₂<...<l_r. 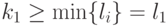Так как системы строк {B₁,B1_2,...,B_r}, {C₁,C₂,...,C_r} линейно выражаются друг через друга, то, в силу леммы 3.5.5 и следствия 3.5.6, k₁=l₁ ( $k_1 \geq \min\{l_i\}=l_1$ ; $l_1 \geq \min\{k_i\}=k_1$ ).
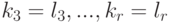Продолжая этот процесс, убеждаемся в том, что $k_3=l_3,...,\allowbreak k_r=l_r$ .
В 2) и 3) доказано, что число ненулевых строк r и номера столбцов l₁,...,l_r, 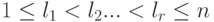$1 \leq l_1<l_2...<l_r \leq n$ , в которых находятся главные неизвестные главных ступенчатых видов B и C, определены однозначно. Таким образом, разбиения на главные и свободные неизвестные, определяемые ступенчатыми видами B и C, совпадают. Поскольку главные неизвестные однозначно выражаются через свободные (в эквивалентных однородных системах линейных уравнений с главными ступенчатыми матрицами B и C ), при этом главный ступенчатый вид определяется этим выражением однозначно (см. замечание 3.6.9, то B=C ).

Замечание 9.5.2 (матричное доказательство п. 4 теоремы о единственности главного ступенчатого вида). Для $A\in M_{m,n}(K)$ существуют такие обратимые матрицы $F,G\in M_m(K)$ (произведения матриц, соответствующих элементарным преобразованиям строк), что

$A=F\cdot B=G\cdot C.$

Следовательно,

$B=D\cdot C,\ \ \text{где}\ \ D=F^{-1}G.$

Используя определение главного ступенчатого вида и переставляя столбцы матриц B и C, имеем:

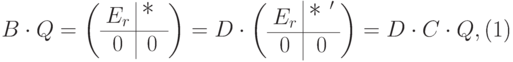$\begin{equation}\label{new7z} B\cdot Q= \left( \begin{array}{c|c} E_r & \text{\large * } \\ \hline 0 & 0 \end{array} \right) = D \cdot \left( \begin{array}{c|c} E_r & \text{\large {*} }' \\ \hline 0 & 0 \end{array} \right) = D\cdot C\cdot Q, \end{equation}$

( 9.1)

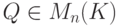где $Q\in M_n(K)$ (матрица Q - обратимая матрица, соответствующая последовательности элементарных преобразований столбцов; мы уже доказали в п. 2 и 3, что числа r и столбцы j₁,...,j_r, в которых стоят лидеры строк, одинаковы для ступенчатых матриц B и C, соответственно; нулевые блоки могут отсутствовать (если k=r=m )). Следовательно, матрица D имеет следующий блочный вид:

$D= \left( \begin{array}{c|c} E_r & \raisebox{-3.5mm}[0pt][0pt]{\text{\large$\tilde{*}$}} \\ \cline{1-1} 0 \end{array} \right),$

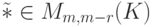где матрица $\tilde * \in M_{m,m-r}(K)$ (если r<m ) состоит из произвольных элементов поля K. Поэтому, умножая D на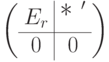

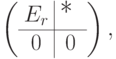
$\left( \begin{array}{c|c} E_r & \text{\large {*} }' \\ \hline 0 & 0 \end{array} \right)$

и приравнивая к

$\left( \begin{array}{c|c} E_r & \text{\large * } \\ \hline 0 & 0 \end{array} \right),$

получаем, что *=*' $\in$ M _{m-r, n-r}. Умножая (9.1) справа на Q^-1, получаем B=C.

Дальше >>

Авторизоваться

Алгебра матриц и линейные пространства

Единственность главного ступенчатого вида матрицы

Единственность главного ступенчатого вида матрицы

Вопросы и ответы