НОУ ИНТУИТ | Алгебра матриц и линейные пространства. Лекция 4: Линейное пространство M

Учитесь и получайте официальные документы БЕСПЛАТНО. Вы можете поддержать наш проект.

Твой путь к знаниям!

Московский государственный университет имени М.В.Ломоносова

Опубликован: 10.09.2007 | Доступ: свободный | Студентов: 4000 / 735 | Оценка: 4.33 / 3.93 | Длительность: 13:22:00

Тема: Математика

Специальности: Математик

Теги: beta, TE, алгебраическим дополнением, вычисления, геометрия, законы дистрибутивности, игры, линейная оболочка строк, матрица перехода, моноид, определитель матрицы, расширенная матрица, система линейных уравнений определенная, собственный вектор, теория, элементы

|

Вам нравится? Нравится 63 студентам

| Поделиться |

Поддержать курс

| Скачать электронную книгу

Аннотация: В данной лекции рассматриваются основные положения и определения алгебры матриц. Рассматривается способ умножения матриц, приведены примеры, доказаны основные теоремы. Также представлены задачи для самостоятельного решения

Ключевые слова: решение системы линейных уравнений, моноид, Законы дистрибутивности, алгебра квадратных матриц

Алгебра матриц

Линейное пространство Mm,n(K) прямоугольных матриц размера mxn

Через M_m,n(K) обозначим совокупность всех прямоугольных матриц над полем K фиксированного размера $m\times n$ (для краткости обозначения, M_n(K)=M_n,n(K) - совокупность всех квадратных $(n\times n)$ -матриц). Как для пространства строк Kⁿ=M_1,n(K) и для пространства столбцов $\hat K^n=M_{n,1}(K)$ , так и для M_m,n(K) определены операции сложения матриц C=A+B ( c_ij=a_ij+b_ij для каждого места (i,j) ) и умножения матрицы на число $c\in K$ D=cA ( d_ij=ca_ij для каждого места (i,j) ). Как и для совокупности строк Kⁿ=M_1,n(K), так и для M_m,n(K) непосредственно проверяется выполнение всех аксиом линейного пространства (в частности, нейтральным элементом в M_m,n(K) будет нулевая матрица 0 с нулями на всех местах, -A=(-1)A ).

Произведение матриц

Если

$A=(a_{ij})\in M_{r,m}(K),\quad B=(b_{ij})\in M_{m,n}(K)$

то мы определили их произведение

$AB=U=(u_{ij})\in M_{r,n}(K),$

полагая

$u_{il}=\sum_{k=1}^{m}a_{ik}b_{kl}$

(т. е. элемент матрицы AB, стоящий на пересечении i -й строки и j -го столбца получается "умножением" i -й строки (длины m ) матрицы A на j -й столбец (длины m ) матрицы B ). Таким образом, условие возможности перемножить две прямоугольные матрицы A и B заключается в том, что длина строк левого множителя A совпадает с длиной столбцов правого множителя B .

Примеры вычисления произведения AB

Пример 8.2.1.

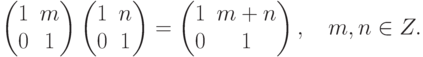
$\begin{pmatrix} 1 & m\\ 0 & 1 \end{pmatrix} \begin{pmatrix} 1 & n\\ 0 & 1 \end{pmatrix} = \begin{pmatrix} 1 & m+n\\ 0 & 1 \end{pmatrix},\quad m,n\in Z.$

Пример 8.2.2.

$\begin{pmatrix} k_1 & ... & k_n \end{pmatrix} \begin{pmatrix} l_1\\ \vdots\\ l_n \end{pmatrix} = \begin{pmatrix} k_1l_1+... k_nl_n \end{pmatrix} \in M_{1}(K)=K.$

Пример 8.2.3.

$\begin{gathe} \begin{pmatrix} \phm 2 & -1\\ \phm 1 & \phm 0\\ -3 & \phm 4 \end{pmatrix} \begin{pmatrix} 1 & -5 & -2\\ 3 & \phm 0 & \phm 4 \end{pmatrix} = \begin{pmatrix} -1 & -10 & -8\\ \phm 1 & -5 & -2\\ \phm 9 & \phm 15 & \phm 22 \end{pmatrix};\\ \begin{pmatrix} 1 & -5 & -2\\ 3 & \phm 0 & \phm 4 \end{pmatrix} \begin{pmatrix} \phm 2 & -1\\ \phm 1 & \phm 0\\ -3 & \phm 4 \end{pmatrix}= \begin{pmatrix} \phm 3 & -9\\ -6 & \phm 13 \end{pmatrix}. \end{gathe}$

Пример 8.2.4. Пусть

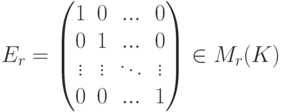
$E_r = \begin{pmatrix} 1 & 0 & ... & 0\\ 0 & 1 & ... & 0\\ \vdots & \vdots & \ddots & \vdots\\ 0 & 0 & ... & 1 \end{pmatrix} \in M_r(K)$

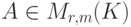(единичная матрица размера $r\times r$ ), $A\in M_{r,m}(K)$ , тогда E_rA=A, AE_m=A. В частности, если E=E_n, $A\in M_n(K)$ , то EA=A=AE.

Матричные единицы Eij

Обозначим через E_ij матрицу, в которой на пересечении i -й строки и j -го столбца стоит 1, а на всех остальных местах стоит 0. Тогда в M_n(K) имеем

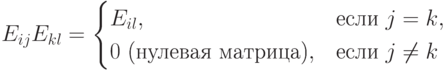
$E_{ij}E_{kl} = \begin{cases} E_{il}, & \text{если } j=k,\\ 0 \text{ (нулевая матрица)}, & \text{если } j\neq k \end{cases}$

(или $E_{ij}E_{kl}=\delta_{jk}E_{il}$ , где

$\delta_{jk} = \begin{cases} 1, & \text{если } j=k,\\ 0, & \text{если } j\neq k \end{cases} \text{ -}$

символ Кронекера).

Важные следствия умножения матричных единиц

Следствие 8.3.1. Так как в M_n(K) при $n \geq 2$

$E_{11}E_{12}=E_{12}\neq 0 = E_{12}E_{11},$

то:

а) умножение матриц некоммутативно;

б) имеются делители нуля (ненулевые элементы, произведение которых равно нулю).

Задача 8.3.2. Найти в M_n(K) все делители нуля. Точнее, доказать, что для $A\in M_n(K)$ следующие условия равносильны:

AX=0 для некоторой матрицы $0\neq X\in M_n(K)$ ;
YA=0 для некоторой матрицы $0\neq Y\in M_n(K)$ ;
|A|=0.

Матрицы элементарных преобразований

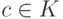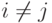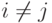Следствие 8.3.3. Пусть $c\in K$ , $i\neq j$ , и

$e_{ij}^c=E+cE_{ij}\in M_m(K)$

(в этой матрице в отличие от единичной матрицы на месте (i,j) вне диагонали стоит c ). Ясно, что $|e_{ij}^c|=1$ .

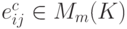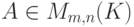а) Если $i\neq j$ , $e_{ij}^c\in M_m(K)$ и $A\in M_{m,n}(K)$ , то матрица $A'=e_{ij}^cA$ получается из матрицы A элементарным преобразованием строк 1-го типа: A'_i=A_i+cA_j.

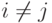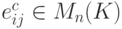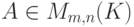б) Если $i\neq j$ , $e_{ij}^c\in M_n(K)$ и $A\in M_{m,n}(K)$ , то матрица 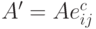$A'=Ae_{ij}^c$ получается из матрицы A элементарным преобразованием столбцов 1-го типа: $\hat A'_j=\hat A_j+c\hat A_i$ .

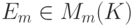Следствие 8.3.4. Пусть $i\neq j$ и t_ij - матрица, полученная из единичной матрицы $E_m\in M_m(K)$ перестановкой i -й и j -й строк (или, что то же самое, перестановкой i -го и j -го столбцов). Ясно, что |t_ij|=-1.

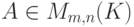а) Если $t_{ij}\in M_m(K)$ и $A\in M_{m,n}(K)$ , то матрица A'=t_ijA получается из матрицы A элементарным преобразованием строк 2-го типа: A'_i=A_j, A'_j=A_i.

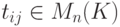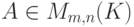б) Если $t_{ij}\in M_n(K)$ и $A\in M_{m,n}(K)$ , то матрица A'=At_ij получается из матрицы A элементарным преобразованием столбцов 2-го типа: $\hat A'_i=\hat A_j$ , $\hat A'_j=\hat A_i$ .

Следствие 8.3.5. Пусть $\lambda_1,...,\lambda_m\in K$ ,

$d(\lambda_1,...,\lambda_m)= \begin{pmatrix} \lambda_1 & 0 & ... & 0\\ 0 & \lambda_2 & ... & 0\\ \vdots & \vdots & \ddots & \vdots\\ 0 & 0 & ... & \lambda_m \end{pmatrix} \in M_{m}(K) \text{ -}$

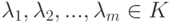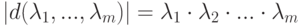диагональная матрица с элементами $\lambda_1,\lambda_2,...,\lambda_m\in K$ на диагонали. Ясно, что $|d(\lambda_1,...,\lambda_m)|= \lambda_1\cdot\lambda_2\cdot...\cdot \lambda_m$ .

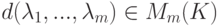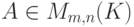а) Если $d(\lambda_1,...,\lambda_m) \in M_{m}(K)$ и $A\in M_{m,n}(K)$ , то

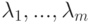$d(\lambda_1,...,\lambda_m)A= \begin{pmatrix} \lambda_1 A_1\\ \lambda_2 A_2\\ \vdots\\ \lambda_m A_m \end{pmatrix} \text{ -}$

матрица, получаемая из матрицы A умножением строк A₁,...,A_m соответственно на "числа" $\lambda_1,...,\lambda_m$ .

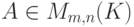б) Если $d(\lambda_1,...,\lambda_n)\in M_{n}(K)$ и $A\in M_{m,n}(K)$ , то

$A\,d(\lambda_1,...,\lambda_n)= (\lambda_1\hat A_1,...,\lambda_n \hat A_n)\text{ -}$

матрица, получаемая из матрицы A умножением столбцов $\hat A_1,...,\hat A_n$ соответственно на "числа" $\lambda_1,...,\lambda_n$ .

В частности, умножение слева матрицы A на матрицу 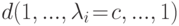$d(1,...,{\lambda_i\!=\!c},...,1)$ , $c\neq 0$ , равносильно применению к строкам матрицы A элементарного преобразования 3-го типа A'_i=cA_i (умножение справа на матрицу такого типа дает применение к столбцам матрицы A элементарного преобразования 3-го типа $\hat A'_i=c\hat A_i$ ).

Замечание 8.3.6. Ясно, что $\lambda E=d(\lambda,...,\lambda)$ и $(\lambda E)A=\lambda A=A(\lambda E)$ для E=E_n, $A\in M_n(K)$ , т. е. \eemph{скалярная} матрица $\lambda E$ перестановочна с любой другой матрицей из M_n(K).

Задача 8.3.7. Пусть K - поле, 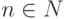$n\in N$ , $n\geq 2$ ,

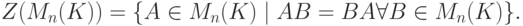
$Z(M_{n}(K))=\{A\in M_{n}(K)\mid AB=BA\kvsp\forall B\in M_{n}(K)\}.$

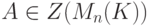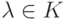Тогда $A\in Z(M_{n}(K))$ в том и только в том случае, когда $A=\lambda E_n$ , $\lambda\in K$ .

Следствие 8.3.8 (матричная запись системы линейных уравнений). Для системы линейных уравнений

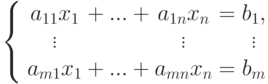
$\left\{ \begin{array}{c@{}c@{}c@{}c@{}c} a_{11}x_1 & {}+...+{} & a_{1n}x_n & {}={} & b_1,\\ \vdots & & \vdots & & \vdots\\ a_{m1}x_1 & {}+...+{} & a_{mn}x_n & {}={} & b_m \end{array} \right.$

возможна матричная запись AX=B, где A=(a_ij) - (m,n) -матрица коэффициентов,

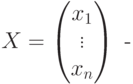
$X= \begin{pmatrix} x_1\\ \vdots\\ x_n \end{pmatrix} \text{ -}$

столбец неизвестных,

$B= \begin{pmatrix} b_1\\ \vdots\\ b_m \end{pmatrix} \in M_{m,1}(K) \text{ -}$

столбец свободных членов.

Таким образом, строка (k₁,...,k_n) является решением системы линейных уравнений, если столбец

$\begin{pmatrix} k_1\\ \vdots\\ k_n \end{pmatrix} \in M_{n,1}(K)$

является решением матричного уравнения

$A \begin{pmatrix} k_1\\ \vdots\\ k_n \end{pmatrix} = \begin{pmatrix} b_1\\ \vdots\\ b_m \end{pmatrix}.$

Замечание 8.3.9 (Штрассен, 1969). Умножение двух $(2\times 2)$ -матриц можно осуществить с использованием 7 умножений и 18 сложений (вместо 8 умножений и 4 сложений в обычном определении произведения матриц

$\begin{pmatrix} a & b\\ c & d \end{pmatrix} \begin{pmatrix} e & f\\ g & h \end{pmatrix} = \left( \begin{smallmatrix} \begin{array}{@{}>{\scriptstyle}l@{}} (a-d)(e-h)+(b-d)(g+h)+{}\\ {}+d(e+g)+(a-b)h \end{array} & -(a-b)h+a(h+f)\\ (-d+c)e+d(e+g) & \begin{array}{@{}>{\scriptstyle}l@{}} (a-d)(e-h)-(a-c)(e+f)+{}\\ {}+a(h+f)-(c-d)e \end{array} \end{smallmatrix}\right).$

Это соображение развивает идею алгоритма А. А. Карацубы (1962 г.) быстрого умножения многочленов. Дальнейший прогресс в теории быстрого умножения чисел, многочленов, матриц связан, в частности, с использованием быстрого преобразования Фурье.

Дальше >>

Алгебра матриц и линейные пространства