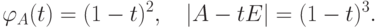Многочлены от матриц, теорема Гамильтона-Кэли. Обратная матрица
Многочлены от матриц, теорема Гамильтона-Кэли
![f(t)=a_0+a_1t+...+a_nt^n\in K[t] \text{ -}](/sites/default/files/tex_cache/2057e6f3cc1db85b16c480400494917e.png)
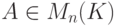 . Тогда определим
. Тогда определим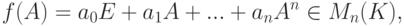
![E=E_n=
\begin{pmatrix}
1 & &
\lefteqn{\raisebox{-5pt}[0pt][0pt]{\text{\hspace*{-10pt}\Large 0 }}}\\ & \ddots\\
\lefteqn{\raisebox{0pt}[0pt][0pt]{\text{\hspace*{0pt}\Large 0 }}}
& & 1
\end{pmatrix} \in M_{n}(K)\text{ -}](/sites/default/files/tex_cache/29b6342a7806e8365396c570bea9ad3a.png)
 -матрица, т. е.
-матрица, т. е.
Пример 8.6.1. Пусть ![f(t)=t^2+2t+1=(t+1)^2, g(t)=t+1\in R[t]](/sites/default/files/tex_cache/c3f7131d3a3bd592a8b4f12550bbc0dd.png) ,
,


Упражнение 8.6.2. Пусть
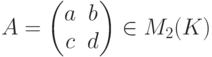
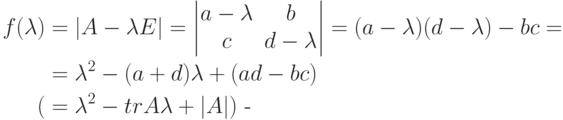
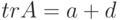 ). Тогда
). Тогда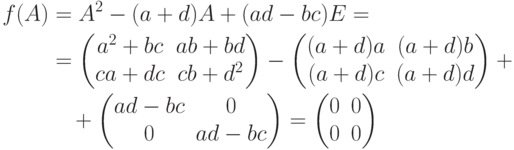
 для
для  -матриц).
-матриц).Теорема 8.6.3. Пусть K - поле,
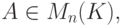
![\Delta_A: K[t]\to M_{n}(K) \text{ -}](/sites/default/files/tex_cache/74147d7b0d14f595f1046327172d4b41.png) отображение, для которого
отображение, для которого 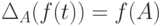 для
для ![f(t)\in K[t]](/sites/default/files/tex_cache/58a962cb10c776f2f89e1085ff6cf7e8.png) . Тогда
. Тогда-
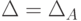 - гомоморфизм K -алгебр, т. е.для всех
- гомоморфизм K -алгебр, т. е.для всех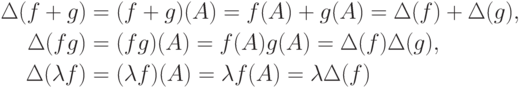
![f,g\in K[t]](/sites/default/files/tex_cache/29c83d191a391a317a2dfef9192178a0.png) ,
, 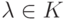 ;
; -
![\Ker \Delta_A = \{f(t)\in K[t]\mid f(A)=0\}](/sites/default/files/tex_cache/57cbb3478384fe2f0e2343e6115d657b.png) - ненулевой идеал кольца K[t].
- ненулевой идеал кольца K[t].
-
Пусть f(t) = a0+a1t+...+antn, g(t) = b0+b1t+...+bmtm, где
 , и пусть
, и пусть 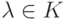 . Тогда
. Тогдаа) если
 , то(здесь bn=...=bm+1=0 );
, то(здесь bn=...=bm+1=0 );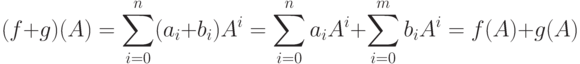
б) если (fg)(t)=c0+c1t+...+cm+ntm+n, где
то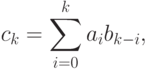 с другой стороны,
с другой стороны,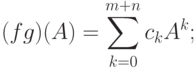 т. е. (fg)(A)=f(A)g(A) ;
т. е. (fg)(A)=f(A)g(A) ;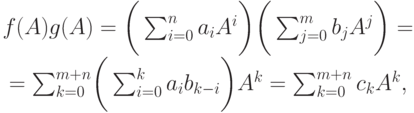
в)

-
Если
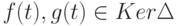 ,
, ![h(t)\in K[t]](/sites/default/files/tex_cache/65a082b2fd3ef1d6d295839679b2a703.png) ,
, 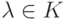 , то f(A)=0, g(A)=0, и поэтомуИтак,
, то f(A)=0, g(A)=0, и поэтомуИтак,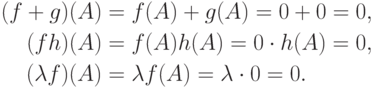
![\Ker\Delta\lhd K[t]](/sites/default/files/tex_cache/f318c4f0efed6cfc2996624e0c2b6823.png) (т. е.
(т. е.  - идеал K -алгебры K[t] ).
- идеал K -алгебры K[t] ).
Так как система матриц
линейно зависима в Mn(K) (поскольку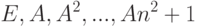
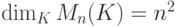 ), то найдутся (не все нулевые) элементы
), то найдутся (не все нулевые) элементы 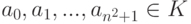 , для которыхт. е.
, для которыхт. е. Итак,
Итак,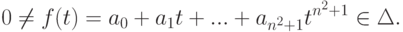
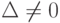 .
.
Замечание 8.6.4. Более сильное утверждение о том, что
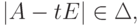
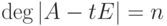 ), таким образом, любая квадратная матрица A является корнем своего характеристического многочлена |A-tE|.
), таким образом, любая квадратная матрица A является корнем своего характеристического многочлена |A-tE|.Теорема 8.6.5 (теорема Гамильтона—Кэли). Пусть K - поле (или даже коммутативное ассоциативное кольцо с 1 ),  ,
, ![p(t)=|A-tE|\in K[t]](/sites/default/files/tex_cache/d419a52ad860f2684da94a0fe7f453bd.png) - характеристический многочлен квадратной матрицы A,
- характеристический многочлен квадратной матрицы A,  . Тогда
. Тогда

![D=A-tE=(d_{ij})\in M_n(K[t]),](/sites/default/files/tex_cache/130d1570e55a16afe9f48211f344305b.png)
![d_{ij}\in K[t]](/sites/default/files/tex_cache/41045669299e2f6b239d2153422fc8f5.png) , рассмотрим присоединенную матрицу
, рассмотрим присоединенную матрицу![B=(b_{ij})\in M_n(K[t]),](/sites/default/files/tex_cache/e88ba9f65e976eb6229edc6d855cec19.png)
![b_{ij}=D_{ji}\in K[t]](/sites/default/files/tex_cache/bd4ccbfc0b929c383ce1678660a9bca9.png) - алгебраическое дополнение элемента d_{ji}. Тогда
- алгебраическое дополнение элемента d_{ji}. Тогда 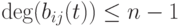 , и поэтому B=B(t)=B0+tB1+...+tn-1Bn-1,
где
, и поэтому B=B(t)=B0+tB1+...+tn-1Bn-1,
где 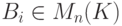 . Так как p(t)=|A-tE|=(-1)ntn+cn-1tn-1+...+c1t+c0,
где
. Так как p(t)=|A-tE|=(-1)ntn+cn-1tn-1+...+c1t+c0,
где  , i=0,1,...,n-1,
, i=0,1,...,n-1,  , то
, то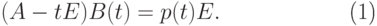 |
( 8.1) |
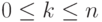 , в левой и правой частях этого равенства, получаем:
, в левой и правой частях этого равенства, получаем: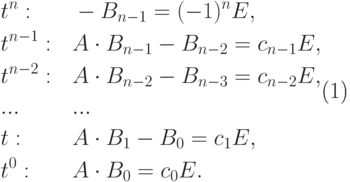 |
( 8.2) |
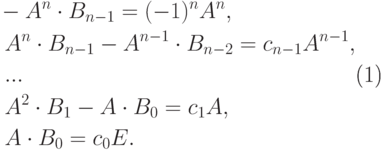 |
( 8.3) |
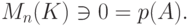
Замечание 8.6.6. Отметим, что равенства (8.2) показывают, что матрицы B0,B1,...,Bn-1 являются многочленами от матрицы A, в частности, BiA=ABi, i=0,1,...,n-1. Поэтому можно было подставить в (8.1) вместо переменной t матрицу A, и тогда
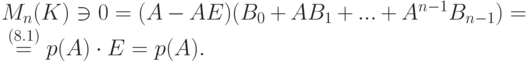
Замечание 8.6.7. Очевидное равенство  не является доказательством теоремы Гамильтона Кэли.
не является доказательством теоремы Гамильтона Кэли.
Упражнение 8.6.8. Аннулирующий многочлен минимальной степени 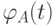 жордановой клетки r -го порядка
жордановой клетки r -го порядка
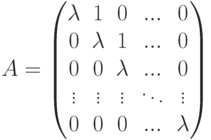
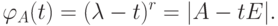
Упражнение 8.6.9. Если