НОУ ИНТУИТ | Алгебра матриц и линейные пространства. Лекция 5: Многочлены от матриц, теорема Гамильтона-Кэли. Обратная матрица

Учитесь и получайте официальные документы БЕСПЛАТНО. Вы можете поддержать наш проект.

Регистрация Вход

Твой путь к знаниям!

Московский государственный университет имени М.В.Ломоносова

Опубликован: 10.09.2007 | Доступ: свободный | Студентов: 4014 / 742 | Оценка: 4.33 / 3.93 | Длительность: 13:22:00

Тема: Математика

Специальности: Математик

|

Вам нравится? Нравится 64 студентам

| Поделиться |

Поддержать курс

| Скачать электронную книгу

Замечания об обратимом (биективном) линейном отображении

Замечание 8.9.1. Пусть U, V - линейные пространства, 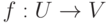$f: U\to V$ - линейное отображение (т. е. f(u₁+u₂)=f(u₁)+f(u₂) и f(ru)=rf(u) для всех $u,u_1,u_2\in U$ и $r\in K)$ . Если отображение f биективно, то его обратное отображение f^-1 также является линейным отображением.

Доказательство. Для всех $v_1,v_2\in V$

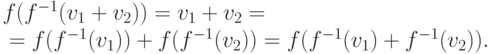
$\begin{mult} f(f^{-1}(v_1+v_2))=v_1+v_2={} \\ {}=f(f^{-1}(v_1))+f(f^{-1}(v_2))= f(f^{-1}(v_1)+f^{-1}(v_2)). \end{mult}$

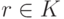Так как f инъективно, то f^-1(v₁+v₂)=f^-1(v₁)+f^-1(v₂). Аналогично, для $v\in V$ и $r\in K$ из f(f^-1(rv))=rv=rf(f^-1(v))=f(rf^-1(v)) следует, что f^-1(rv)=rf^-1(v). Итак, f^-1 - линейное отображение.

Замечание 8.9.2. Если $f: \hat K^n\to\hat K^m$ - линейное отображение с матрицей $F=(f_{ij})\in M_{m,n}(K)$ , то f - биективное отображение тогда и только тогда, когда

а) m=n,

б) $|F|\neq 0$ .

При этом матрица линейного отображения g=f^-1 равна G=F^-1.

Доказательство.

Если m=n и $|F|\neq 0$ , то для системы
$\left\{ \begin{array}{@{}l@{}} f_{11}x_1 +...+ f_{1n}x_n = y_1,\\ \dotfill\\ f_{n1}x_1 +...+ f_{nn}x_n = y_n \end{array} \right.$
по правилу Крамера знаем, что решение существует и единственно, при этом
$x_i=\frac{D_i}{|F|}= \frac{F_{1i}}{|F|}y_1+...+\frac{F_{ni}}{|F|}y_n= g_{i1}y_1+...+g_{in}y_n,$
где G=(g_ij)=F^-1. Итак, g=f^-1 существует и является линейным отображением с матрицей G=F^-1.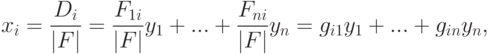
Для линейного отображения $f: \hat K^n\to\hat K^m$ с матрицей $F=(f_{ij})\in M_{m,n}(K)$ , где
$f \begin{pmatrix} x_1\\ \vdots\\ x_n \end{pmatrix} = \begin{pmatrix} y_1\\ \vdots\\ y_m \end{pmatrix},\quad \left\{ \begin{array}{@{}l@{}} f_{11}x_1 +...+ f_{1n}x_n = y_1,\\ \dotfill\\ f_{m1}x_1 +...+ f_{mn}x_n = y_m, \end{array} \right.$
из нашего исследования систем линейных уравнений (метод Гаусса) имеем: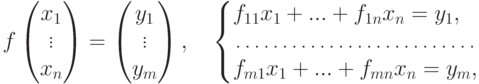

а) если m<n, то отображение f не является инъективным (даже для нулевого столбца свободных членов есть отличный от нуля прообраз (ненулевое решение));

б) если m>n, то отображение f не является сюръективным (так как если $m>n\geq r$ , то в ступенчатой форме F нашей системы для столбца правых частей, дающего "экзотическое" уравнение $0x_1+...+0x_n=\bar y_m\neq 0$ , уже нет прообраза (решения)).

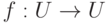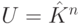Итак, если f биективно, то m=n, т. е. $f: U\to U$ , где $U=\hat K^n$ . Если g=f^-1, то g - линейное отображение. Пусть G=(g_ij) - его матрица. Так как fg=1_U=gf, то FG=E=GF, и поэтому $|F|\neq 0$ и G=F^-1.

Упражнение 8.9.3 (еще одна очень хорошая функция от матриц).

Пусть $A=(a_{ij})\in M_n(K)$ . Положим
$tr(A)= a_{11}+a_{22}+...+a_{nn}=\sum\limits_{i=1}^n a_{ii}$
(след матрицы A ). Тогда:
а) - линейная функция,
$tr(A+B)=tr(A)+tr(B),\quad tr(\lambda A)=\lambda\tr(A)$
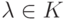для всех $A,B\in M_n(K)$ и $\lambda\in K$ ;

б) tr(E)=n ;

в) .
Функция $tr: M_n(K)\to K$ однозначно определяется свойствами а), б) и в).
Если (например, K= R ), то в алгебре матриц M_n(K) единичная матрица E не представима в виде AB-BA для $A,B\in M_n(K)$ .

Матричное построение поля комплексных чисел

Поле комплексных чисел C можно найти как изоморфное подполе в кольце $(2\times 2)$ -матриц M_2( R) над полем действительных чисел R.

Рассмотрим совокупность C' всех $(2\times 2)$ -матриц вида

$\begin{pmatrix} \phm a & b\\ -b & a \end{pmatrix} \in M_{2}( R),$

где $a,b\in R$ . Так как

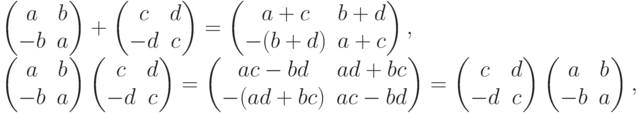
$\begin{gathe} \begin{pmatrix} \phm a & b\\ -b & a \end{pmatrix} + \begin{pmatrix} \phm c & d\\ -d & c \end{pmatrix} = \begin{pmatrix} a+c & b+d\\ -(b+d) & a+c \end{pmatrix},\\ \begin{pmatrix} \phm a & b\\ -b & a \end{pmatrix} \begin{pmatrix} \phm c & d\\ -d & c \end{pmatrix} = \begin{pmatrix} ac-bd & ad+bc\\ -(ad+bc) & ac-bd \end{pmatrix} = %{} %\\ %&= \begin{pmatrix} \phm c & d\\ -d & c \end{pmatrix} \begin{pmatrix} \phm a & b\\ -b & a \end{pmatrix}, \end{gathe}$

то подмножество C' в M₂( R) замкнуто относительно операций сложения и умножения, о которых мы уже знаем, что они ассоциативны, умножение в C' коммутативно, сложение и умножение связаны законом дистрибутивности.

Так как

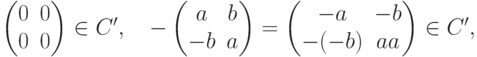
$\begin{pmatrix} 0 & 0\\ 0 & 0 \end{pmatrix} \in C',\quad -\begin{pmatrix} \phm a & b\\ -b & a \end{pmatrix} = \begin{pmatrix} -a & -b\\ -(-b) & aa \end{pmatrix} \in C',$

то ( C',+) - абелева группа.

Итак, $( C',{+},{\cdot})$ - коммутативное кольцо.

Если

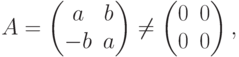
$A= \begin{pmatrix} \phm a & b\\ -b & a \end{pmatrix} \neq \begin{pmatrix} 0 & 0\\ 0 & 0 \end{pmatrix},$

то

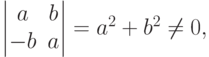
$\begin{vmatrix} \phm a & b\\ -b & a \end{vmatrix} = a^2+b^2\neq 0,$

и поэтому существует обратная матрица

$A^{-1} = \begin{pmatrix} \frac{a}{a^2+b^2} & \frac{-b}{a^2+b^2}\\[3mm] -\left(\frac{-b}{a^2+b^2}\right) & \frac{a}{a^2+b^2} \end{pmatrix} \in C',$

таким образом, C' - поле (подполе в кольце матриц M₂( R) ).

Отождествляя действительное число 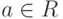$a\in R$ со скалярной матрицей

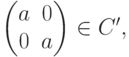
$\begin{pmatrix} a & 0\\ 0 & a \end{pmatrix} \in C',$

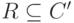получаем (изоморфное) вложение поля R в C' ( $R\subseteq C'$ ),

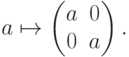
$a \mapsto \begin{pmatrix} a & 0\\ 0 & a \end{pmatrix}.$

Обозначив

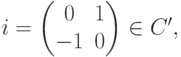
$i = \begin{pmatrix} \phm 0 & 1\\ -1 & 0 \end{pmatrix} \in C',$

получаем

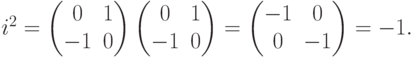
$i^2 = \begin{pmatrix} \phm 0 & 1\\ -1 & 0 \end{pmatrix} \begin{pmatrix} \phm 0 & 1\\ -1 & 0 \end{pmatrix} = \begin{pmatrix} -1 & \phm 0\\ \phm 0 & -1 \end{pmatrix} = -1.$

Если

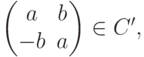
$\begin{pmatrix} \phm a & b\\ -b & a \end{pmatrix} \in C',$

то

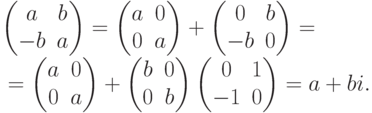
$\begin{mult} \begin{pmatrix} \phm a & b\\ -b & a \end{pmatrix} = \begin{pmatrix} a & 0\\ 0 & a \end{pmatrix} + \begin{pmatrix} \phm 0 & b\\ -b & 0 \end{pmatrix} ={} \\ {}= \begin{pmatrix} a & 0\\ 0 & a \end{pmatrix} + \begin{pmatrix} b & 0\\ 0 & b \end{pmatrix} \begin{pmatrix} \phm 0 & 1\\ -1 & 0 \end{pmatrix} = a+bi. \end{mult}$

Замечание 8.10.1. Фактически, нами установлено, что отображение f из C в C',

$f((a,b)) = \begin{pmatrix} \phm a & b\\ -b & a \end{pmatrix}$

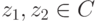является изоморфизмом построенных полей C и C', т. е. биекцией, для которой f(z₁+z₂)=f(z₁)+f(z₂), f(z₁z₂)=f(z₁)f(z₂) для всех $z_1,z_2\in C$ .

Дальше >>

Авторизоваться

Алгебра матриц и линейные пространства

Многочлены от матриц, теорема Гамильтона-Кэли. Обратная матрица

Замечания об обратимом (биективном) линейном отображении

Матричное построение поля комплексных чисел

Вопросы и ответы