|
С помощью обобщенного алгоритма Евклида найдите числа х и у, удовлетворяющие уравнению 30х +12y = НОД(30,12). х=1, у=-2, НОД = 6. Где ошибка? |
Шифрование, помехоустойчивое кодирование и сжатие информации
Принципы сжатия данных
Как было сказано выше, одной из важных задач предварительной подготовки данных к шифрованию является уменьшение их избыточности и выравнивание статистических закономерностей применяемого языка. Частичное устранение избыточности достигается путём сжатия данных.
Сжатие информации представляет собой процесс преобразования исходного сообщения из одной кодовой системы в другую, в результате которого уменьшается размер сообщения. Алгоритмы, предназначенные для сжатия информации, можно разделить на две большие группы: реализующие сжатие без потерь (обратимое сжатие) и реализующие сжатие с потерями (необратимое сжатие).
Обратимое сжатие подразумевает абсолютно точное восстановление данных после декодирования и может применяться для сжатия любой информации. Оно всегда приводит к снижению объема выходного потока информации без изменения его информативности, то есть без потери информационной структуры. Более того, из выходного потока, при помощи восстанавливающего или декомпрессирующего алгоритма, можно получить входной, а процесс восстановления называется декомпрессией или распаковкой и только после процесса распаковки данные пригодны для обработки в соответствии с их внутренним форматом. Сжатие без потерь применяется для текстов, исполняемых файлов, высококачественного звука и графики.
Необратимое сжатие имеет обычно гораздо более высокую степень сжатия, чем кодирование без потерь, но допускает некоторые отклонения декодированных данных от исходных. На практике существует широкий круг практических задач, в которых соблюдение требования точного восстановления исходной информации после декомпрессии не является обязательным. Это, в частности, относится к сжатию мультимедийной информации: звука, фото- или видеоизображений. Так, например, широко применяются форматы мультимедийной информации JPEG и MPEG, в которых используется необратимое сжатие. Необратимое сжатие обычно не используется совместно с криптографическим шифрованием, так как основным требованием к криптосистеме является идентичность расшифрованных данных исходным. Однако при использовании мультимедиа-технологий данные, представленные в цифровом виде, часто подвергаются необратимой компрессии перед подачей в криптографическую систему для шифрования. После передачи информации потребителю и расшифрования мультимедиа-файлы используются в сжатом виде (то есть не восстанавливаются).
Рассмотрим подробнее некоторые из наиболее распространённых способов обратимого сжатия данных.
Наиболее известный простой подход и алгоритм сжатия информации обратимым путем – это кодирование серий последовательностей (Run Length Encoding – RLE). Суть методов данного подхода состоит в замене цепочек или серий повторяющихся байтов на один кодирующий байт-заполнитель и счетчик числа их повторений. Проблема всех аналогичных методов заключается лишь в определении способа, при помощи которого распаковывающий алгоритм мог бы отличить в результирующем потоке байтов кодированную серию от других, – не кодированных последовательностей байтов. Решение проблемы достигается обычно простановкой меток вначале кодированных цепочек. Такими метками могут быть характерные значения битов в первом байте кодированной серии, значения первого байта кодированной серии. Недостатком метода RLE является достаточно низкая степень сжатия или стоимость кодирования файлов с малым числом серий и, что еще хуже – с малым числом повторяющихся байтов в сериях.
При равномерном кодировании информации на сообщение отводится одно и то же число бит, независимо от вероятности его появления. Вместе с тем логично предположить, что общая длина передаваемых сообщений уменьшится, если часто встречающиеся сообщения кодировать короткими кодовыми словами, а редко встречающиеся – более длинными. Возникающие при этом проблемы связаны с необходимостью использования кодов с переменной длиной кодового слова. Существует множество подходов к построению подобных кодов.
Одними из широко используемых на практике являются словарные методы, к основным представителям которых относятся алгоритмы семейства Зива и Лемпела. Их основная идея заключается в том, что фрагменты входного потока ("фразы") заменяются указателем на то место, где они в тексте уже ранее появлялись. В литературе подобные алгоритмы обозначаются как алгоритмы LZ сжатия.
Подобный метод быстро приспосабливается к структуре текста и может кодировать короткие функциональные слова, так как они очень часто в нем появляются. Новые слова и фразы могут также формироваться из частей ранее встреченных слов. Декодирование сжатого текста осуществляется напрямую, – происходит простая замена указателя готовой фразой из словаря, на которую тот указывает. На практике LZ-метод добивается хорошего сжатия, его важным свойством является очень быстрая работа декодера.
Другим подходом к сжатию информации является код Хаффмана, кодер и декодер которого имеют достаточно простую аппаратную реализацию. Идея алгоритма состоит в следующем: зная вероятности вхождения символов в сообщение, можно описать процедуру построения кодов переменной длины, состоящих из целого количества битов. Символам с большей вероятностью присваиваются более короткие коды, тогда как реже встречающимся символам – более длинные. За счет этого достигается сокращение средней длины кодового слова и большая эффективность сжатия. Коды Хаффмана имеют уникальный префикс (начало кодового слова), что и позволяет однозначно их декодировать, несмотря на их переменную длину.
Процедура синтеза классического кода Хаффмана предполагает наличие априорной информации о статистических характеристиках источника сообщений. Иначе говоря, разработчику должны быть известны вероятности возникновения тех или иных символов, из которых образуются сообщения. Рассмотрим синтез кода Хаффмана на простом примере.
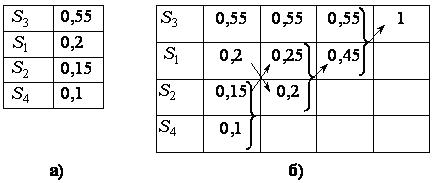
Пусть источник информации способен генерировать четыре различных символа S1…S4 с вероятностями возникновения p(S1)=0,2, p(S2)=0,15, p(S3)=0,55, p(S4)=0,1. Отсортируем символы по убыванию вероятности появления и представим в виде таблицы ( рис. 14.3, а).
Процедура синтеза кода состоит из трех основных этапов. На первом происходит свертка строк таблицы: две строки, соответствующие символам с наименьшими вероятностями возникновения заменяются одной с суммарной вероятностью, после чего таблица вновь переупорядочивается. Свертка продолжается до тех пор, пока в таблице не останется лишь одна строка с суммарной вероятностью, равной единице ( рис. 14.3, б).
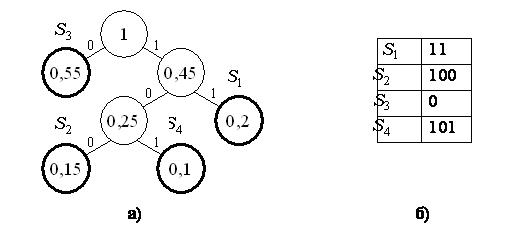
На втором этапе осуществляется построение кодового дерева по свернутой таблице ( рис. 14.4, а). Дерево строится, начиная с последнего столбца таблицы.
Корень дерева образует единица, расположенная в последнем столбце. В рассматриваемом примере эта единица образуется из вероятностей 0,55 и 0,45, изображаемых в виде двух узлов дерева, связанных с корнем. Первый из них соответствует символу S3 и, таким образом, дальнейшее ветвление этого узла не происходит.
Второй узел, маркированный вероятностью 0,45, соединяется с двумя узлами третьего уровня, с вероятностями 0,25 и 0,2. Вероятность 0,2 соответствует символу S1, а вероятность 0,25, в свою очередь, образуется из вероятностей 0,15 появления символа S2 и 0,1 появления символа S4.
Ребра, соединяющие отдельные узлы кодового дерева, нумеруются цифрами 0 и 1 (например, левые ребра – 0, а правые – 1 ). На третьем, заключительном этапе, строится таблица, в которой сопоставляются символы источника и соответствующие им кодовые слова кода Хаффмана. Эти кодовые слова образуются в результате считывания цифр, которыми помечены ребра, образующие путь от корня дерева к соответствующему символу. Для рассматриваемого примера код Хаффмана примет вид, показанный в таблице справа ( рис. 14.4, б).
Однако классический алгоритм Хаффмана имеет один существенный недостаток. Для восстановления содержимого сжатого сообщения декодер должен знать таблицу частот, которой пользовался кодер. Следовательно, длина сжатого сообщения увеличивается на длину таблицы частот, которая должна посылаться впереди данных, что может свести на нет все усилия по сжатию сообщения.
Другой вариант статического кодирования Хаффмана заключается в просмотре входного потока и построении кодирования на основании собранной статистики. При этом требуется два прохода по файлу – один для просмотра и сбора статистической информации, второй – для кодирования. В статическом кодировании Хаффмана входным символам (цепочкам битов различной длины) ставятся в соответствие цепочки битов также переменной длины – их коды. Длина кода каждого символа берется пропорциональной двоичному логарифму его частоты, взятому с обратным знаком. А общий набор всех встретившихся различных символов составляет алфавит потока.
Существует другой метод – адаптивного или динамического кодирования Хаффмана. Его общий принцип состоит в том, чтобы менять схему кодирования в зависимости от характера изменений входного потока. Такой подход имеет однопроходный алгоритм и не требует сохранения информации об использованном кодировании в явном виде. Адаптивное кодирование может дать большую степень сжатия, по сравнению со статическим, поскольку более полно учитываются изменения частот входного потока. При использовании адаптивного кодирования Хаффмана усложнение алгоритма состоит в необходимости постоянной корректировки дерева и кодов символов основного алфавита в соответствии с изменяющейся статистикой входного потока.
Методы Хаффмана дают достаточно высокую скорость и умеренно хорошее качество сжатия. Однако кодирование Хаффмана имеет минимальную избыточность при условии, что каждый символ кодируется в алфавите кода символа отдельной цепочкой из двух бит – {0, 1}. Основным же недостатком данного метода является зависимость степени сжатия от близости вероятностей символов к 2 в некоторой отрицательной степени, что связано с тем, что каждый символ кодируется целым числом бит.
Совершенно иное решение предлагает арифметическое кодирование. Этот метод основан на идее преобразования входного потока в одно число с плавающей запятой. Арифметическое кодирование является методом, позволяющим упаковывать символы входного алфавита без потерь при условии, что известно распределение частот этих символов.
Предполагаемая требуемая последовательность символов при сжатии методом арифметического кодирования рассматривается как некоторая двоичная дробь из интервала [0, 1). Результат сжатия представляется как последовательность двоичных цифр из записи этой дроби. Идея метода состоит в следующем: исходный текст рассматривается как запись этой дроби, где каждый входной символ является "цифрой" с весом, пропорциональным вероятности его появления. Этим объясняется интервал, соответствующий минимальной и максимальной вероятностям появления символа в потоке.
Рассмотренные методы обеспечивают обратимое сжатие данных. На практике применяются как программные, так и аппаратные их реализации, позволяющие добиваться коэффициентов сжатия порядка 20-40% в зависимости от типа сжимаемой информации.
Таким образом, криптографическое шифрование, помехоустойчивое кодирование и сжатие отчасти дополняют друг друга и их комплексное использование помогает эффективно использовать каналы связи для надежной защиты передаваемой информации.
Ключевые термины
Избыточность – характеристика помехоустойчивого кода, показывающая, насколько увеличена длина кодового слова по сравнению с обычным непомехоустойчивым кодом. Для многих помехоустойчивых кодов избыточность можно определить как отношение числа контрольных разрядов к общему числу разрядов кодового слова.
Код – совокупность знаков, а также система правил, позволяющая представлять информацию в виде набора таких знаков.
Кодовое слово – любой ряд допустимых знаков в соответствии с используемой системой правил.
Минимальное кодовое расстояние – наименьшее из всех расстояний по Хэммингу для любых пар различных кодовых слов, образующих код.
Помехоустойчивый код – код, позволяющий обнаруживать и корректировать ошибки при хранении и передаче сообщений.
Расстояние по Хэммингу – число разрядов кодовых слов, в которых они различны.
Сжатие информации – процесс преобразования исходного сообщения из одной кодовой системы в другую, в результате которого уменьшается размер сообщения.
Соседние кодовые слова – кодовые слова, отличающиеся значением только одного разряда.
Краткие итоги
В теории информации выделяют три вида преобразования информации: криптографическое шифрование, помехоустойчивое кодирование и сжатие (или эффективное кодирование). Общим для всех трех видов преобразования является то, что информация каким-либо образом меняет форму представления, но не смысл. Отличия разных видов кодирования связаны с целью проводимых преобразований.
Так, целью криптографического преобразования является, как известно, защита от несанкционированного доступа, аутентификация и защита от преднамеренных изменений. Помехоустойчивое кодирование выполняется с целью защиты информации от случайных помех при передаче и хранении. Для этого при записи и передаче в полезные данные добавляют специальным образом структурированную избыточную информацию, а при чтении (приёме) её используют для того, чтобы обнаружить или исправить ошибки. Естественно, что число ошибок, которое можно исправить, ограничено и зависит от конкретного применяемого кода.
Эффективное кодирование (или сжатие информации) представляет собой процесс преобразования исходного сообщения из одной кодовой системы в другую, в результате которого уменьшается размер сообщения. Алгоритмы сжатия информации делятся на две группы: алгоритмы сжатия без потерь (обратимого сжатия) и алгоритмы сжатия с потерями (необратимого сжатия). За счет эффективного кодирования уменьшается избыточность сообщений, что позволяет производить более надежное криптографическое шифрование информации.
Таким образом, криптографическое шифрование, помехоустойчивое кодирование и сжатие отчасти дополняют друг друга и их комплексное использование помогает эффективно использовать каналы связи для надежной защиты передаваемой информации.
Набор для практики
Вопросы для самопроверки
- Какие виды преобразований информации используются для комплексной защиты информации?
- Каковы основные принципы помехоустойчивого кодирования сообщений?
- Каким образом используется синдром ошибки при кодировании сообщений кодом Хэмминга?
- Приведите примеры кодов, обеспечивающих сжатие сообщений.
- За счет чего достигается сжатие сообщений при кодировании методом Хаффмана?
- Как формируется кодовое слова Хаффмана?
- Для каких типов данных целесообразно использовать алгоритмы сжатия с потерями? С чем это связано?
Упражнения для самопроверки
- Блоковый помехоустойчивый код имеет длину блока 8 бит. Его избыточность равна 25%. Чему равно число информационных разрядов в нем?
- Пусть источник информации способен генерировать четыре различных символа S1…S4 с вероятностями возникновения p(S1)=0,1, p(S2)=0,3, p(S3)=0,5, p(S4)=0,1. По этим данным выполните синтез классического кода Хаффмана.
Заключение
В данном курсе были рассмотрены наиболее распространенные в настоящее время методы криптографической защиты информации. Но криптографическая наука, как и любая другая наука, не стоит на месте, а продолжает развиваться. Не прекращаются усилия специалистов по созданию новых методов криптографической защиты информации.
Новая "отрасль" криптографии – асимметричная криптография стала всем уже привычной. Несмотря на то, что открыто уже более десятка алгоритмов шифрования с открытым ключом, продолжается поиск новых методов асимметричного шифрования. Так, например, алгоритмы на эллиптических кривых были предложены учеными только в самом конце ХХ века, а в настоящее время они уже активно используются на практике.
Другая сравнительно молодая ветвь криптографии – исследование криптографических протоколов. Несмотря на то, что первые протоколы появились во второй половине ХХ века, на настоящий момент имеется уже несколько десятков различных типов криптографических протоколов. Криптографические протоколы являются одним из основных объектов исследования теоретической криптографии. Ежегодно специалистами предлагаются новые криптографические протоколы, и задача криптоаналитиков заключается в том, чтобы верно оценить надежность каждого из протоколов.
Одной из относительно новых разработок криптографии является квантовая криптография, основанная на определенных явлениях квантовой физики. Информацию в квантовых системах предлагается передавать по оптоволоконным каналам с помощью квантов света – фотонов, меняющих свое состояние при попытке их перехватить и измерить. Утверждается, что, используя квантовые явления, можно спроектировать и создать такую систему связи, которая всегда сможет обнаруживать подслушивание. Практическая реализация квантовой криптографии пока что находится на самом начальном уровне и встречает множество трудностей.
Таким образом, криптографические методы не прекращают развиваться. Они широко используются и будут использоваться в составе средств комплексной защиты информации.