|
С помощью обобщенного алгоритма Евклида найдите числа х и у, удовлетворяющие уравнению 30х +12y = НОД(30,12). х=1, у=-2, НОД = 6. Где ошибка? |
Поточные шифры и генераторы псевдослучайных чисел. Часть 1
Цель лекции: познакомиться с понятием "поточный шифр", а также с принципами использования генераторов псевдослучайных ключей при потоковом шифровании
Поточные шифры
Блочный алгоритм предназначен для шифрования блоков определенной длины. Однако может возникнуть необходимость шифрования данных не блоками, а, например, по символам. Поточный шифр (stream cipher) выполняет преобразование входного сообщения по одному биту (или байту) за операцию. Поточный алгоритм шифрования устраняет необходимость разбивать сообщение на целое число блоков достаточно большой длины, следовательно, он может работать в реальном времени. Таким образом, если передается поток символов, каждый символ может шифроваться и передаваться сразу.
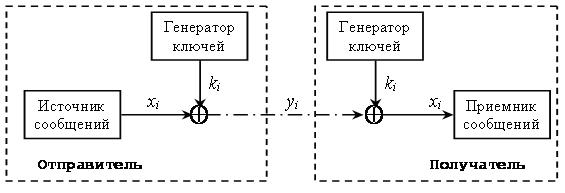
Работа типичного поточного шифра представлена на рис. 7.1.
Генератор ключей выдает поток битов ki, которые будут использоваться в качестве гаммы. Источник сообщений генерирует биты открытого текста хi, которые складываются по модулю 2 с гаммой, в результате чего получаются биты зашифрованного сообщения уi:
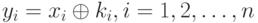
Чтобы из шифротекста y1, y2,..., yn восстановить сообщение x1, x2,..., xn, необходимо сгенерировать точно такую же ключевую последовательность k1, yk,..., kn, что и при шифровании, и использовать для расшифрования формулу
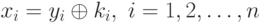
Обычно исходное сообщение и ключевая последовательность представляют собой независимые потоки бит. Таким образом, так как шифрующее (и расшифрующее) преобразование для всех поточных шифров одно и то же, они должны различаться только способом построения генераторов ключей. Получается, что безопасность системы полностью зависит от свойств генератора потока ключей. Если генератор потока ключей выдает последовательность, состоящую только из одних нулей (или из одних единиц), то зашифрованное сообщение будет в точности таким же, как и исходный поток битов (в случае единичных ключей зашифрованное сообщение будет инверсией исходного). Если в качестве гаммы используется один символ, представленный, например, восемью битами, то хотя зашифрованное сообщение и будет внешне отличаться от исходного, безопасность системы будет очень низкой. В этом случае при многократном повторении кода ключа по всей длине текста существует опасность его раскрытия статистическим методом. Поясним это на простом примере цифрового текста, закрытого коротким цифровым кодом ключа методом гаммирования.
Пример. Пусть известно, что исходное сообщение представляло собой двоично-десятичное число, то есть число, каждая тетрада (четыре бита) которого получена при переводе десятичной цифры 0...9 в двоичный вид. Перехвачено 24 бита зашифрованного сообщения Y, то есть шесть тетрад Y1, Y2, Y3, Y4, Y5, Y6, а именно значение 1100 1101 1110 1111 0000 0001. Известно, что ключ шифрования состоял из четырех бит, которые тоже представляют собой однозначное десятичное число, то есть одно и то же значение 0?K?9 использовалось для шифрования каждых четырех бит исходного сообщения. Таким образом, шифрование числа X1, X2, X3, X4, X5, X6 ключом К можно представить в виде системы уравнений:
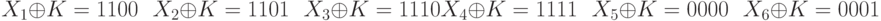
Исходя из условия, что Хi принимает десятичные значения от 0 до 9, для поиска неизвестного К определим все возможные значения X1’; и К, сумма которых по модулю 2 приводит к результату 1100:
K = 0000 0001 0010 0011 0100 0101 0110 0111 1000 1001 Y1 = 1100 1100 1100 1100 1100 1100 1100 1100 1100 1100 --------------------- X1’ = 1100 1101 1110 1111 1000 1001 1010 1011 0100 0101
Так как исходное значение состояло из цифр от 0 до 9, то можно исключить из рассмотрения значения ключа 0000, 0001, 0010, 0011, 0110, 0111, так при сложении с ними получаются значения большие 9 в десятичном эквиваленте. Такие значения не могли присутствовать в открытом тексте. Таким образом, первый этап анализа уже позволил сократить количество возможных ключей с десяти до четырех.
Для дальнейшего поиска неизвестного К определим все возможные значения X2’; и оставшихся вариантов ключа, сумма которых по модулю 2 приводит к результату Y2 = 1101:
K = 0100 0101 1000 1001 Y2 = 1101 1101 1101 1101 --------------------- X2’ = 1001 1000 0101 0100
Видно, что этот этап не позволил отбросить ни одного из оставшихся вариантов ключа. Попытаемся это сделать, используя Y3=1110:
K = 0100 0101 1000 1001 Y3 = 1110 1110 1110 1110 --------------------- X2’ = 1010 1011 0110 0111
После проведения этого этапа становится ясно, что ключом не могли быть значения 0100 и 0101. Остается два возможных значения ключа: 1000(2)=8(10) и 1001(2)=9(10).
Дальнейший анализ по данной методике в данном случае, к сожалению, не позволит однозначно указать, какой же из двух полученных вариантов ключа использовался при шифровании. Однако можно считать успехом уже то, что пространство возможных ключей снизилось с десяти до двух. Остается попробовать каждый из двух найденных ключей для дешифровки сообщений и проанализировать смысл полученных вскрытых текстов.
В реальных случаях, когда исходное сообщение составлено не только из одних цифр, но и из других символов, использование статистического анализа позволяет быстро и точно восстановить ключ и исходные сообщения при короткой длине ключа, закрывающего поток секретных данных.
Принципы использования генераторов псевдослучайных чисел при потоковом шифровании
Современная информатика широко использует псевдослучайные числа в самых разных приложениях — от методов математической статистики и имитационного моделирования до криптографии. При этом от качества используемых генераторов псевдослучайных чисел (ГПСЧ) напрямую зависит качество получаемых результатов.
ГПСЧ могут использоваться в качестве генераторов ключей в поточных шифрах. Целью использования генераторов псевдослучайных чисел является получение "бесконечного" ключевого слова, располагая относительно малой длиной самого ключа. Генератор псевдослучайных чисел создает последовательность битов, похожую на случайную. На самом деле, конечно же, такие последовательности вычисляются по определенным правилам и не являются случайными, поэтому они могут быть абсолютно точно воспроизведены как на передающей, так и на принимающей стороне. Последовательность ключевых символов, использующаяся при шифровании, должна быть не только достаточно длинной. Если генератор ключей при каждом включении создает одну и ту же последовательность битов, то взломать такую систему также будет возможно. Следовательно, выход генератора потока ключей должен быть функцией ключа. В этом случае расшифровать и прочитать сообщения можно будет только с использованием того же ключа, который использовался при шифровании.
Для использования в криптографических целях генератор псевдослучайных чисел должен обладать следующими свойствами:
- период последовательности должен быть очень большой;
- порождаемая последовательность должна быть "почти" неотличима от действительно случайной;
- вероятности порождения различных значений должны быть в точности равны;
- для того, чтобы только законный получатель мог расшифровать сообщение, следует при получении потока ключевых битов ki использовать и учитывать некоторый секретный ключ, причем вычисление числа ki+1 по известным предыдущим элементам последовательности ki без знания ключа должно быть трудной задачей.
При наличии указанных свойств последовательности псевдослучайных чисел могут быть использованы в поточных шифрах.