|
С помощью обобщенного алгоритма Евклида найдите числа х и у, удовлетворяющие уравнению 30х +12y = НОД(30,12). х=1, у=-2, НОД = 6. Где ошибка? |
Алгоритм криптографического преобразования данных ГОСТ 28147-89
Цель лекции: изучение блочного алгоритма шифрования по ГОСТ 28147-89.
Основные сведения
В России в качестве стандарта на блочные алгоритмы шифрования с закрытым ключом в 1989 году был принят ГОСТ 28147-89. Он рекомендуется к использованию для криптографической защиты данных. Шифр, предлагаемый ГОСТ 28147-89 построен по тем же принципам, что и американский DES, однако по сравнению с DES отечественный стандарт шифрования более удобен для программной реализации.
В отличие от американского DES в отечественном стандарте применяется более длинный ключ – 256 бит. Кроме того, российский стандарт предлагает использовать 32 раунда шифрования, тогда как DES – только 16.
Таким образом, основные параметры алгоритма криптографического преобразования данных ГОСТ 28147-89 следующие: размер блока составляет 64 бита, размер ключа – 256 бит, количество раундов – 32.
Алгоритм представляет собой классическую сеть Фейштеля. Шифруемый блок данных разбивается на две одинаковые части, правую R и левую L. Правая часть складывается с подключом раунда и посредством некоторого алгоритма шифрует левую часть. Перед следующим раундом левая и правая части меняются местами. Такая структура позволяет использовать один и тот же алгоритм как для шифрования, так и для дешифрования блока.
В алгоритме шифрования используются следующие операции:
- сложение слов по модулю 232;
- циклический сдвиг слова влево на указанное число бит;
- побитовое сложение по модулю 2;
- замена по таблице.
На различных шагах алгоритмов ГОСТа данные, которыми они оперируют, интерпретируются и используются различным образом. В некоторых случаях элементы данных обрабатываются как массивы независимых битов, в других случаях – как целое число без знака, в третьих – как имеющий структуру сложный элемент, состоящий из нескольких более простых элементов.
Структура раунда ГОСТ 28147-89
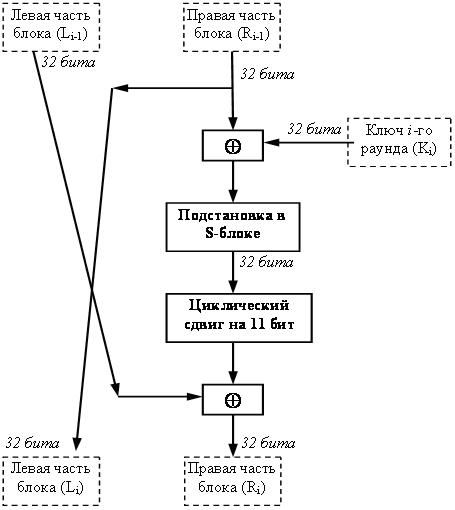
Структура одного раунда ГОСТ 28147-89 приведена на рис. 5.1.
Шифруемый блок данных разбивается на две части, которые затем обрабатываются как отдельные 32-битовые целые числа без знака. Сначала правая половина блока и подключ раунда складываются по модулю 232. Затем производится поблочная подстановка. 32-битовое значение, полученное на предыдущем шаге (обозначим его S), интерпретируется как массив из восьми 4-битовых блоков кода: S=(S0,S1,S2,S3,S4,S5,S6,S7). Далее значение каждого из восьми блоков заменяется на новое, которое выбирается по таблице замен следующим образом: значение блока Si заменяется на Si-тый по порядку элемент (нумерация с нуля) i-го узла замен (т.е. i-той строки таблицы замен, нумерация также с нуля). Другими словами, в качестве замены для значения блока выбирается элемент c номером строки, равным номеру заменяемого блока, и номером столбца, равным значению заменяемого блока как 4-битового целого неотрицательного числа. В каждой строке таблицы замен записаны числа от 0 до 15 в произвольном порядке без повторений. Значения элементов таблицы замен взяты от 0 до 15, так как в четырех битах, которые подвергаются подстановке, может быть записано целое число без знака в диапазоне от 0 до 15. Например, первая строка S-блока может содержать такие значения: 5, 8, 1, 13, 10, 3, 4, 2, 14, 15, 12, 7, 6, 0, 9, 11. В этом случае значение блока S0 (четыре младших бита 32-разрядного числа S) заменится на число, стоящее на позиции, номер которой равен значению заменяемого блока. Если S0 = 0, то оно заменится на 5, если S0= 1, то оно заменится на 8 и т.д.
После выполнения подстановки все 4-битовые блоки снова объединяются в единое 32-битное слово, которое затем циклически сдвигается на 11 битов влево. Наконец, с помощью побитовой операции "сумма по модулю 2" результат объединяется с левой половиной, вследствие чего получается новая правая половина Ri. Новая левая часть Li берется равной младшей части преобразуемого блока: Li= Ri-1.
Полученное значение преобразуемого блока рассматривается как результат выполнения одного раунда алгоритма шифрования.
Процедуры шифрования и расшифрования
ГОСТ 28147-89 является блочным шифром, поэтому преобразование данных осуществляется блоками в так называемых базовых циклах. Базовые циклы заключаются в многократном выполнении для блока данных основного раунда, рассмотренного нами ранее, с использованием разных элементов ключа и отличаются друг от друга порядком использования ключевых элементов. В каждом раунде используется один из восьми возможных 32-разрядных подключей.
Рассмотрим процесс создания подключей раундов. В ГОСТ эта процедура очень проста, особенно по сравнению с DES. 256-битный ключ K разбивается на восемь 32-битных подключей, обозначаемых K0, K1, K2,K3, K4, K5, K6, K7. Алгоритм включает 32 раунда, поэтому каждый подключ при шифровании используется в четырех раундах в последовательности, представленной на таблица 5.1.
| Раунд | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| Подключ | K0 | K1 | K2 | K3 | K4 | K5 | K6 | K7 |
| Раунд | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 |
| Подключ | K0 | K1 | K2 | K3 | K4 | K5 | K6 | K7 |
| Раунд | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| Подключ | K0 | K1 | K2 | K3 | K4 | K5 | K6 | K7 |
| Раунд | 25 | 26 | 27 | 28 | 29 | 30 | 31 | 32 |
| Подключ | K7 | K6 | K5 | K4 | K3 | K2 | K1 | K0 |
Процесс расшифрования производится по тому же алгоритму, что и шифрование. Единственное отличие заключается в порядке использования подключей Ki. При расшифровании подключи должны быть использованы в обратном порядке, а именно, как указано на таблица 5.2.
| Раунд | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| Подключ | K7 | K6 | K5 | K4 | K3 | K2 | K1 | K0 |
| Раунд | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 |
| Подключ | K7 | K6 | K5 | K4 | K3 | K2 | K1 | K0 |
| Раунд | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| Подключ | K7 | K6 | K5 | K4 | K3 | K2 | K1 | K0 |
| Раунд | 25 | 26 | 27 | 28 | 29 | 30 | 31 | 32 |
| Подключ | K7 | K6 | K5 | K4 | K3 | K2 | K1 | K0 |