|
С помощью обобщенного алгоритма Евклида найдите числа х и у, удовлетворяющие уравнению 30х +12y = НОД(30,12). х=1, у=-2, НОД = 6. Где ошибка? |
Принципы построения блочных шифров с закрытым ключом
Требования к блочному алгоритму шифрования
К современным алгоритмам блочного шифрования предъявляют достаточно жесткие требования, связанные с областью применения, возможностью реализации на различных вычислительных платформах и другими факторами. Рассмотрим основные из требований.
- Алгоритм должен обеспечивать высокий уровень стойкости, и эта стойкость не должна основываться на сохранении втайне самого алгоритма.
- Незначительное изменение исходного сообщения должно приводить к существенному изменению зашифрованного сообщения даже при использовании одного и того же ключа.
- Алгоритм должен успешно противостоять атакам по выбранному тексту, то есть таким, чтобы нельзя было узнать ключ, даже зная достаточно много пар (зашифрованное сообщение, незашифрованное сообщение), полученных при шифровании с использованием данного ключа.
- Алгоритм шифрования должен иметь возможность быть реализованым на различных платформах, которые предъявляют различные требования. Для наиболее быстрых приложений используется специальная аппаратура. Несмотря на это, программные реализации применяются также достаточно часто. Поэтому алгоритм должен допускать эффективную программную реализацию на универсальных микропроцессорах. Алгоритм должен также работать на микроконтроллерах и других процессорах среднего размера.
- Алгоритм должен использовать простые операции, которые эффективны на микропроцессорах, т.е. исключающее или, сложение, табличные подстановки, умножение по модулю. Не должно использоваться сдвигов переменной длины, побитных перестановок или условных переходов.
- Алгоритм должен эффективно реализовываться на специализированной аппаратуре, предназначенной для выполнения операций шифрования и расшифрования, то есть реализация алгоритма в виде электронных устройств должна быть экономичной.
- Алгоритм шифрования должен быть применим во многих приложениях. Алгоритм должен быть эффективен при шифровании файлов данных или большого потока данных, при создании определенного количества случайных битов, а также должна быть возможность его использования для формирования односторонней хеш-функции1Хэш-функция – это математическая или иная функция, которая для строки произвольной длины вычисляет некоторое целое значение или некоторую другую строку фиксированного размера. Хеш-функции более подробно рассматриваются в "Криптографические хеш-функции" .
- Алгоритм должен быть простым для написания кода, чтобы минимизировать вероятность программных ошибок. Также это дает возможность анализа и уменьшает закрытость алгоритма.
- Алгоритм должен допускать любую случайную строку битов нужной длины в качестве возможного ключа (это называется иметь плоское пространство ключей ). Не должно быть "слабых" ключей, облегчающих криптоанализ.
- Алгоритм должен легко модифицироваться для различных уровней безопасности и удовлетворять как минимальным, так и максимальным требованиям.
Некоторое уточнение необходимо сделать относительно пункта 1, требующего высокую криптостойкость алгоритма шифрования. Обычно под "высокой криптостойкостью" понимают, что шифр должен быть стоек по отношению к атаке по выбранному тексту. Это автоматически подразумевает его стойкость по отношению к атакам по шифротексту и по известному тексту. Однако известно, что при атаке по выбранному тексту шифр всегда может быть взломан путем перебора ключей. Поэтому требование стойкости шифра можно уточнить следующим образом: "Шифр стоек (при атаке по выбранному тексту), если для него не существует алгоритма взлома, существенно более быстрого, чем прямой перебор ключей". Интересно, что по состоянию на сегодняшний день ни для одного используемого шифра не доказано строго соответствие этому определению стойкости.
Сеть Фейштеля
На рис. 3.1 была представлена общая структура блочного алгоритма шифрования. Понятно, что само преобразование данных выполняется в раундах или шагах шифрования. Какие же действия надо выполнить в одном раунде, чтобы в результате выполнения всего алгоритма получить надежно зашифрованные данные?
Большой вклад в исследования принципов разработки блочных шифров внес американский ученый Х. Фейштель (Horst Feistel). Он, в частности, принимал участие в разработке системы шифрования "Люцифер" фирмы IBM. Фейштель предложил структуру, называемую в настоящее время сетью Фейштеля. Сети Фейштеля получили широкое распространение, так как, с одной стороны, они удовлетворяют всем требованиям к алгоритмам симметричного шифрования, а с другой стороны, достаточно просты и удобны в использовании.
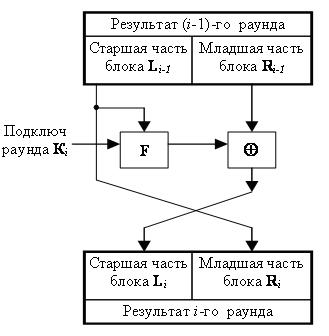
Раунд, организованный по сети Фейштеля имеет следующую структуру. Входной блок делится на несколько частей равной длины. Эти части блока называются ветвями. Так, например, если блок имеет длину 64 бита, используются две ветви по 32 бита каждая. Ветви обрабатываются по отдельности, после чего осуществляется циклический сдвиг всех ветвей влево. В случае двух ветвей каждый раунд имеет структуру, показанную на рис. 3.2
Функция F называется образующей. Каждый раунд состоит из вычисления функции F для одной ветви и побитового выполнения операции "сумма по модулю 2" результата F с другой ветвью. После этого ветви меняются местами. Число раундов может быть различным для разных алгоритмов. В некоторых алгоритмах рекомендуется от 8 до 32 раундов, в других – больше. В целом увеличение количества раундов увеличивает криптостойкость алгоритма. Возможно, эта особенность и повлияла на столь активное распространение сети Фейштеля, так как для большей криптостойкости достаточно просто увеличить количество раундов, не изменяя сам алгоритм. В последнее время количество раундов не фиксируется, а лишь указываются рекомендуемые пределы.
В последнее время все чаще используются различные разновидности сети Фейштеля для 128-битного блока с четырьмя ветвями. Увеличение количества ветвей, а не размерности каждой ветви связано с тем, что наиболее популярными до сих пор остаются процессоры с 32-разрядными словами, следовательно, оперировать 32-разрядными словами эффективнее, чем с 64-разрядными.
В блочных алгоритмах, построенных на основе сети Фейштеля, основной операцией является вычисление образующей функции F. Эта функция использует подключ раунда и одну ветвь входного блока для вычисления результата. Именно тем, как определяется функция F, системы шифрования и отличаются друг от друга. В некоторых алгоритмах введены также начальные преобразования входного блока данных, придающие некоторую "случайность" входному тексту (это называется рандомизацией данных.) Рандомизация производится для того, чтобы уменьшить естественную избыточность входного сообщения.
В следующих лекциях рассматриваются некоторые используемые на практике блочные алгоритмы симметричного шифрования. Их описание в данном курсе лекций нельзя считать абсолютно полным, например, по приведенным описаниям трудно составить программы шифрования/расшифрования. Это связано с ограничением на объем данного учебного пособия. Однако все основные этапы рассматриваемых алгоритмов в учебном пособии приведены, так же как и особенности реализации и применения.
Ключевые термины
Комбинированный (композиционный) шифр – криптографическое преобразование данных, получаемое в результате комбинации нескольких подряд примененных простых шифров.
Ключ – информация, необходимая для шифрования и расшифрования сообщений.
Шифр – совокупность заранее оговоренных способов преобразования исходного секретного сообщения с целью его защиты.
Шифрование с закрытым ключом (симметричное шифрование) – методы обратимого преобразования данных, в которых используется один и тот же ключ, который обе стороны информационного обмена должны хранить в секрете от противника. Все известные из истории шифры, например, шифр Цезаря – это шифры с закрытым ключом.
Краткие итоги
В симметричных блочных шифрах используется комбинация нескольких простейших операций над цепочками или блоками бит: сложения по модулю 2, сложения по модулю 216 или 232, циклического сдвига, замены и перестановки. Для повышения криптостойкости эти операции выполняются циклически несколько раз, образуя раунды или шаги. На стойкость шифра влияют такие факторы, как размер блока, размер ключа, количество раундов шифрования.
Алгоритмы симметричного шифрования различаются способом, которым обрабатывается исходный текст. Возможно шифрование блоками или шифрование потоком. Блок текста рассматривается как неотрицательное целое число либо как несколько независимых неотрицательных целых чисел. Длина блока всегда выбирается равной степени двойки, например, 64, 128, 256 бит.
Блочный алгоритм симметричного шифрования может иметь в своей основе сеть (схему) Фейштеля. В этом случае входной блок делится на несколько частей равной длины (ветви). Ветви обрабатываются по отдельности, после чего осуществляется циклический сдвиг всех ветвей влево.
Набор для практики
Вопросы для самопроверки
- Какой шифр называют комбинированным или композиционным шифром?
- Какие факторы влияют на стойкость блочного алгоритма шифрования?
- Какие простейшие операции применяются в блочных алгоритмах шифрования?
- В чем отличие блочных алгоритмов шифрования от поточных?
- Что понимается под "раундом" алгоритма шифрования?
- Каковы требования к блочному алгоритму шифрования?
- Почему блочный алгоритм шифрования должен иметь простую и понятную структуру?
- Что понимается под требованием "высокой криптостойкости" алгоритма шифрования?
- Что представляет собой сеть Фейштеля?
Упражнения для самопроверки
- Сложите по модулю 2:
- двоичные числа 10101100 и 11001010 ;
- десятичные числа 15 и 10 ;
- шестнадцатеричные числа 0В5 и 37.
- Сложите по модулю 28:
- двоичные числа 10101100 и 11001010 ;
- десятичные числа 155 и 100 ;
- шестнадцатеричные числа 0В5 и 37.
- Выполните операцию циклического сдвига:
- влево на 5 разрядов для двоичного числа 10101100 ;
- вправо на 4 разряда для шестнадцатеричного числа 9E ;
- вправо на 2 разряда для шестнадцатеричного числа 55.
- Пусть каждые три бита входного сообщения заменяются по следующей таблице замен:
Выполните разбиение исходного сообщения на блоки по три бита и произведите поблочную замену для следующих сообщений,
представленных в цифровом виде:
- 1010 1100 1100(2)
- 2356(10)
- 0В57(16)