Математические методы описания моделей конструкций РЭС. Элементы теории графов
17. 2. Части графа
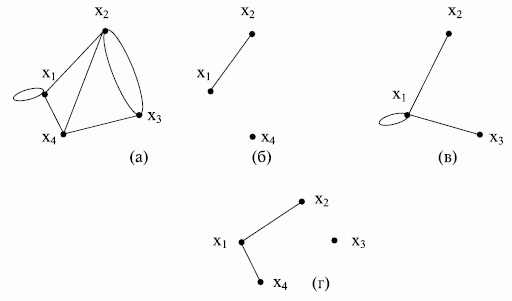
Граф 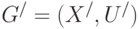 является частью графа
является частью графа 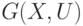 , если
, если 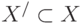 и
и 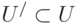 , т.е. граф содержит все вершины и рёбра любой его части.
, т.е. граф содержит все вершины и рёбра любой его части.
Часть, которая наряду с некоторым подмножеством рёбер графа содержит и все инцидентные им вершины, называется подграфом.
Часть, которая наряду с некоторым подмножеством рёбер графа содержит все вершины графа (  ,
, 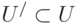 ), называется суграфом.
), называется суграфом.
Исходный граф по отношению к его подграфу называют надграфом, а по отношению к суграфу - сверхграфом.
Совокупность всех рёбер графа, не принадлежащих его подграфу (вместе с инцидентными вершинами ), образует дополнение подграфа (рис. 17.12).
Связный неориентированный граф, не содержащий циклов, называют деревом.
Несвязный граф без циклов, отдельные компоненты связности которого являются деревьями, называют лесом.
Все приведённые деревья изоморфны друг другу, т.е. на трёх вершинах можно построить только одно неизоморфное дерево.
17. 3. Способы задания графов
Уже отмечалось, что произвольный граф можно задать совокупностью двух множеств:  - множества вершин и
- множества вершин и  - множества рёбер ( дуг ) графа или множества
- множества рёбер ( дуг ) графа или множества  и отображения
и отображения 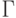 множества
множества  в
в 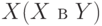 .
.
Условные обозначения таких графов 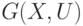 и
и 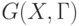 , соответственно.
, соответственно.
Другой удобной формой описания графов является представление их с помощью матриц, методика формальной разработки которых хорошо разработана.
Матрица смежности
Из ранее сказанного известно, что две вершины 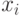 и
и  графа
графа 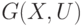 называются смежными, если они являются граничными вершинами ребра
называются смежными, если они являются граничными вершинами ребра 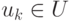 .
.
Отношение смежности на множестве вершин графа можно определить, представив каждое ребро как пару смежных вершин, т.е.
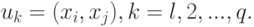
Для неориентированных графов такие пары неупорядочены, так что
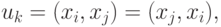
а для орграфов - упорядочены, причём, 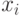 и
и  означают, соответственно, начальную и конечную вершины дуги
означают, соответственно, начальную и конечную вершины дуги 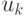 .
Петля при вершине
.
Петля при вершине  в обоих случаях представляется неупорядоченной парой
в обоих случаях представляется неупорядоченной парой 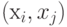 .
.
Множество вершин  вместе с определённым на нём отношением смежности полностью определяет граф.
вместе с определённым на нём отношением смежности полностью определяет граф.
Граф можно представить матрицей смежности.
Строки и столбцы матрицы соответствуют вершинам графа, а её 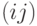 элемент равен числу кратных рёбер, связывающих вершины
элемент равен числу кратных рёбер, связывающих вершины 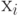 и
и  (или направленных от вершины
(или направленных от вершины 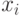 к вершине
к вершине  для орграфов).
для орграфов).
Например, для графа рис. 17.2, а, матрица смежности имеет вид
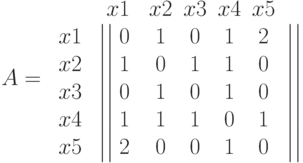
Матрица смежности неориентированного графа всегда симметрична, а орграфа - в общем случае несимметрична. Неориентированным рёбрам соответствуют пары ненулевых элементов, симметричных относительно главной диагонали матрицы, а петлям - ненулевые элементы главной диагонали.
В столбцах и строках, соответствующих изолированным вершинам, все элементы равны нулю. Элементы матрицы простого графа равны 0 или 1, причём, элементы главной диагонали равны 0.
Правильность составления матрицы легко проверить: для неориентированного графа сумма элементов в каждом i -том столбце или строке соответствует степени вершины 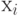 . Если элементы матрицы
. Если элементы матрицы  расположенные на главной диагонали, отличны от нуля, то это свидетельствует о наличии петель в вершине
расположенные на главной диагонали, отличны от нуля, то это свидетельствует о наличии петель в вершине 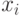 .
.
Для неориентированного графа матрица смежности  симметрична относительно главной диагонали, так как
симметрична относительно главной диагонали, так как  .
.
При решении целого класса задач проектирования РЭС приходится оперировать матрицами, которые строятся аналогично матрицам смежности, но значения их элементов определяются мерой (весом), связанной с ребром ( дугой ) графа.
В САПР широко используют две разновидности таких матриц: матрицу весовых соотношений и матрицу длин.
Матрица весовых соотношений
Это квадратная матрица 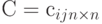 , общий элемент которой
, общий элемент которой
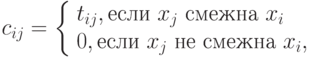
где 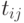 - вес связи
- вес связи 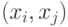 .
.
Применение матриц весовых соотношений позволяет учитывать различные требования к сокращению длины тех или иных электрических соединений в конструкциях РЭС, условия тепловой и электромагнитной совместимости отдельных элементов схемы и другие.
Это квадратная матрица 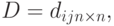 общий элемент которой
общий элемент которой
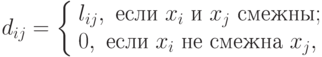
В евклидовой метрике расстояние между двумя точками на плоскости
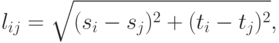
где  и
и 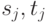 - координаты вершин
- координаты вершин  и
и  , соответственно.
, соответственно.
Это выражение неудобно для использования в машинных программах, так как извлечение квадратного корня на ЭВМ требует больших затрат времени. Поэтому часто пользуются линейной метрикой, тем более, что при решении многих конструкторских задач она вполне оправдана.
Пример. При проектировании многослойных печатных плат трассировка соединений ведётся в каждом из слоёв во взаимно перпендикулярных направлениях, в связи с чем длина электрических связей между элементами с координатами 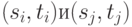
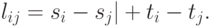
Линейная метрика оказывается непригодной для решения задач, в которых имеет место вычисление производных по координатам (оптимизация нелинейных функций).
В этом случае расстояние между двумя точками представляется в виде степенной функции:
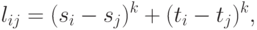
где  - показатель степени (как правило,
- показатель степени (как правило,  ).
).
Матрицу длин используют при решении задач оптимизации размещения конструктивных элементов на плате, когда одним из критериев качества является минимум суммарной длины соединений.
Матрица инцидентности
Если вершина 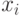 является концом ребра
является концом ребра  то говорят, что они инцидентны: вершина
то говорят, что они инцидентны: вершина 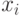 инцидентна ребру
инцидентна ребру 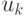 и ребро
и ребро 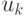 инцидентно вершине. В то время как смежность представляет собой отношение между однородными объектами ( вершинами ), инцидентность - это отношение между разнородными объектами ( вершинами и рёбрами).
инцидентно вершине. В то время как смежность представляет собой отношение между однородными объектами ( вершинами ), инцидентность - это отношение между разнородными объектами ( вершинами и рёбрами).
При рассмотрении орграфов различают положительную инцидентность ( дуга исходит из вершины ) и отрицательную инцидентность ( дуга заходит в вершину ).
Рассматривая инцидентность вершин и рёбер графа, можно представить его матрицей инцидентности размера  , строки которой соответствуют вершинам, а столбцы - рёбрам.
, строки которой соответствуют вершинам, а столбцы - рёбрам.
Для неориентированного графа элементы этой матрица определяются по следующему правилу: ij - элемент равен 1, если вершина 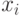 инцидентна ребру
инцидентна ребру 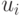 и равен нулю, если
и равен нулю, если 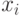 и
и  не инцидентны.
не инцидентны.
В случае орграфа ненулевой 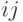 - элемент равен
- элемент равен  , если
, если 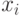 - начальная вершина дуги
- начальная вершина дуги  , и равен
, и равен 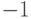 , если
, если 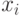 - конечная вершина дуги
- конечная вершина дуги  .
.
Приведём пример: составим матрицу инцидентности для рис. 17.2,а.

Каждый столбец матрицы содержит обязательно два единичных элемента (для орграфа эти элементы всегда имеют различные знаки и равны, соответственно,  и
и 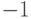 ).
).
Количество единиц в строке равно степени соответствующей вершины (для орграфа количество положительных единиц определяет положительную степень, а количество отрицательных единиц - отрицательную степень).
Нулевая строка соответствует изолированной вершине, а нулевой столбец - петле.
Следует иметь в виду, что нулевой столбец матрицы инцидентности лишь указывает на наличие петли, но не содержит сведений том, с какой вершиной эта петля связана (в практических приложениях это может быть несущественно).
Правильность составления матрицы 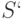 легко проверить: число единиц в i-ой строке матрицы соответствует степени вершины
легко проверить: число единиц в i-ой строке матрицы соответствует степени вершины 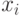 графа, а число единиц в каждом столбце - двум, так как каждое ребро соединяет две вершины графа. Единственное исключение составляет петля, дважды инцидентная одной и той же вершине.
графа, а число единиц в каждом столбце - двум, так как каждое ребро соединяет две вершины графа. Единственное исключение составляет петля, дважды инцидентная одной и той же вершине.
Столбец, соответствующий петле, состоит из нулей, в результате чего матрица  не указывает на существование петель. Поэтому при изучении свойств графа с помощью этой матрицы необходимо исключить из него петли.
не указывает на существование петель. Поэтому при изучении свойств графа с помощью этой матрицы необходимо исключить из него петли.
Граф однозначно задаётся матрицами смежности и инцидентности. В свою очередь, каждая из этих матриц полностью определяет граф.
Существуют простые приёмы перехода от одной матрицы к другой.
Кроме выше перечисленных разновидностей матриц используются также матрицы контуров, сечений и так далее. Эти матрицы используются, как правило, при анализе электронных схем, поэтому далее они не будут рассматриваться.
Контрольные вопросы
- На какие понятия опираются понятия теории графов?
- Для каких целей используются графы?
- Сформулируйте понятие графа.
- Как представляется граф геометрически?
- Что представляют собой ориентированные и неориентированные графы?
- В каких случаях и почему используются ориентированные и неориентированные графы?
- Какие вершины называют смежными?
- Какие вершины называют инцидентными?
- Что называют локальной степенью вершины?
- Что называют несвязным графом?
- Что называют маршрутом?
- Что входит в понятие " цепь "?
- Как составляется матрица смежности графа?
- Как составляется матрица инцидентности?

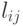 - длина
- длина 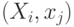 .
.