Разработка "сквозных" математических моделей технологического процесса как основа АСНИ
Проверка гипотезы нормального распределения исходной информации
Эта работа должна проводиться с целью корректного перехода к построению математических моделей (ММ). Дело в том, что используемый для построения ММ корреляционно-регрессионный анализ предполагает, что собранная для построения ММ информация должна подчиняться нормальному закону распределения. Поэтому на данном этапе необходима проверка гипотезы о нормальном законе распределения информации, собранной по результатам пассивного или активного эксперимента.
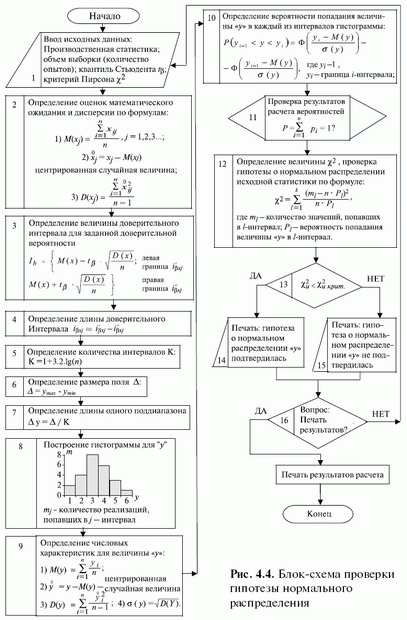
Априори выдвигается гипотеза о нормальном законе ее распределения. Затем осуществляется проверка этой гипотезы (рис. 4.4).
Если гипотеза не подтвердилась, то увеличивают объем выборки (количество измерений) до тех пор, пока не получим нормальный закон распределения. В данном случае используется свойство нормального закона: он является предельным для других законов, т. е. с увеличением объема выборки другие законы стремятся к нормальному закону распределения.
Если гипотеза подтвердилась, то можно переходить к построению математической модели, в частности, использовать метод наименьших квадратов при поиске коэффициентов уравнений регрессии.
Преобразование распределений к нормальному закону
Если исследователь, использовав методы, изложенные ранее, убедился, что гипотеза нормальности распределения не может быть принята, то, возможно, с помощью существующих методов удастся так преобразовать исходные данные, что их распределение будет подчиняться нормальному закону. После получения окончательного результата необходимо выполнить обратное преобразование.
В самом начале операции преобразования данных большую помощь могут оказать гистограмма и полигон распределения. При обработке результатов наблюдений в медицине, биологии, материаловедении, экономике и других отраслях знаний встречаются логарифмические нормальные распределения, особенностью которых является крутая левая ветвь полигона и пологая правая (полигон явно асимметричен). Логарифмические нормальные распределения играют большую роль в математической статистике, так как встречаются очень часто в практике обработки наблюдений и легко преобразуются к нормальному распределению.
При логарифмировании исходных данных левая ветвь кривой распределения сильно растягивается, и распределение принимает приближенно нормальный характер. Если при преобразовании 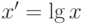 получаются значения, расположенные между 0 и 1, то все вновь полученные значения для удобства расчетов и во избежание получения отрицательных параметров необходимо умножить на 10 в соответствующей степени, чтобы все цифры были больше единицы, т. е. выполнить преобразование
получаются значения, расположенные между 0 и 1, то все вновь полученные значения для удобства расчетов и во избежание получения отрицательных параметров необходимо умножить на 10 в соответствующей степени, чтобы все цифры были больше единицы, т. е. выполнить преобразование 
Асимметричное распределение с одной вершиной часто приводится к нормальному преобразованием 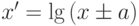 . В отдельных случаях можно применять и другие преобразования:
. В отдельных случаях можно применять и другие преобразования:
- обратная величина
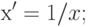
( 4.12) - обратное значение квадратных корней
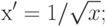
( 4.13)
Преобразование "обратная величина" является наиболее "сильным". Среднее положение между логарифмическим преобразованием и "обратной величиной" занимает преобразование "обратное значение квадратных корней".
Для нормализации смещенного вправо распределения служат тригонометрические преобразования, а также степенные преобразования  .
При этом
.
При этом  принимают значения:
принимают значения: 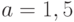 при умеренном и
при умеренном и 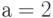 при сильно выраженном правом смещении.
при сильно выраженном правом смещении.
Известны случаи, когда нормальный закон распределения не удается получить вообще.
Однако мы будем исходить из случаев, для которых закон больших чисел выполняется.
Контрольные вопросы
- Какие исходные данные необходимы для построения математических моделей?
- Какие схемы используются при построении математических моделей?
- Привести примеры определения контрольных точек и контролируемых параметров.
- Какие параметры называют информативными?
- Обосновать применение статистических методов для построения математических моделей технологических процессов.
- Что называется внешним проектированием?
- Что называют внутренним проектированием?
- Почему необходима предварительная обработка производственной информации?
- В чем сущность предварительной обработки производственной информации?
- Что принимается за грубые погрешности?
- Как учитываются грубые погрешности?
- Почему необходима проверка гипотезы о нормальном законе распределения исходной информации?
- Почему производственная информация должна подчиняться нормальному закону распределения?
- Как осуществляется проверка гипотезы о нормальном законе распределения?
- Как используется квантиль Стьюдента при проверке гипотезы?
- Как используется критерий Пирсона при проверке гипотезы?
- Что называется центрированной случайной величиной?
- Почему при расчете математического обеспечения, дисперсии и среднеквадратического отклонения говорят об их оценках?
- Запишите и поясните формулу для определения доверительного интервала.
- Покажите, как строится гистограмма и какова ее роль при проверке гипотезы.
- Опишите процедуру проверки гипотезы о нормальном распределении по блок-схеме (рис. 4.4).
- Как используется критерий Пирсона?
- Каковы выводы следует сделать в случае, если гипотеза о нормальном распределении подтвердилась?
- Какие меры следует применять, если гипотеза не подтвердилась?
- Какое свойство нормального закона распределения используется при проверке гипотезы?
- Какие преобразования используются для получения нормального закона распределения?