НОУ ИНТУИТ | Моделирование систем. Лекция 10: Планирование активного эксперимента при поиске оптимальных условий

Учитесь и получайте официальные документы БЕСПЛАТНО. Вы можете поддержать наш проект.

Регистрация Вход

Твой путь к знаниям!

Мордовский государственный университет имени Н.П. Огарева

Опубликован: 30.11.2010 | Доступ: свободный | Студентов: 3371 / 2064 | Оценка: 4.12 / 4.13 | Длительность: 14:37:00

ISBN: 978-5-9963-0352-6

Темы: Программирование, Алгоритмы и дискретные структуры

Специальности: Программист, Системный архитектор

|

Вам нравится? Нравится 32 студентам

| Поделиться |

Поддержать курс

| Скачать электронную книгу

Практическая часть

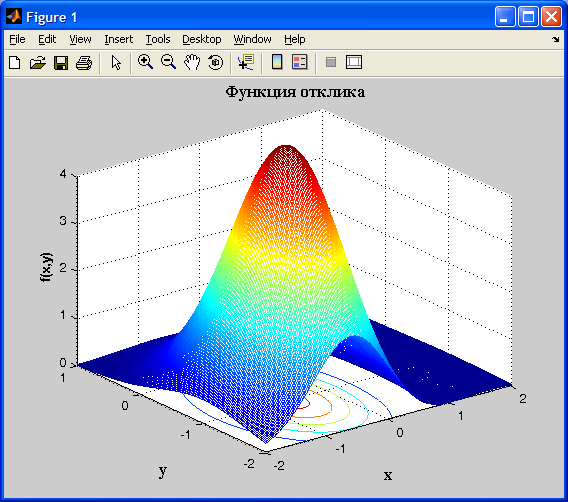
Рассмотрим процесс моделирования крутого восхождения (наискорейшего подъема) к экстремуму функции отклика. Для методической ясности проведения активного эксперимента зададим аналитический вид функции двух переменных

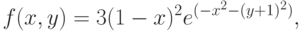$f(x,y)=3(1-x)^2 e^{(-x^2-(y+1)^2)},$

( 10.13)

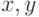где x, y — независимые переменные, факторы.

Графический образ функции двух переменных (10.13) показан на рис. 10.1.

Рис. 10.1. Исследуемая функция отклика

Необходимые измерения функции отклика при движении по градиенту будем проводить по аналитическому выражению (10.13).

В каждой точке факторного пространства заданную функцию отклика (10.13) будем аппроксимировать линейной моделью — линейным уравнением регрессии вида

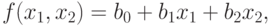( 10.14)

где 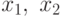$x_{1},\mbox{ }x_{2}$ — факторы.

Коэффициенты 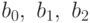$b_{0},\mbox{ }b_{1},\mbox{ }b_{2}$ в (10.14) определяются в постановке двухфакторного эксперимента.

Программный код моделирования крутого восхождения к экстремуму функции отклика может быть следующим:

function active;
clc,close all
syms x y
zz = 3*(1-x)^2*exp(-x^2 - (y+1)^2);
fprintf('\n\t Аналитический вид функции отклика:\n')
fprintf('\t f(x,y) = %s\n',char(zz))

% РАСЧЕТ ОПТИМАЛЬНЫХ КООРДИНАТ ФУНКЦИИ ОТКЛИКА
xy = fminsearch(@pan1,[0;0]);
fprintf('\t Оптимальные значения факторов:\n')
fprintf('\t x_optim = %g\n\t y_optim = %g\n',xy(1),xy(2))
y_max = abs(pan1(xy));
fprintf('\t Значение макcимума аналитической функции отклика:\n')
fprintf('\t f(x,y)_max = %g\n',y_max)
% ПОСТРОЕНИЕ ФУНКЦИИ ОТКЛИКА В ПРОСТРAНСТВЕ
[x1,x2] = meshgrid(-2:0.02:2,-2:0.02:1);
z =  3*(1-x1).^2.*exp(-x1.^2 - (x2+1).^2);
meshc(x1,x2,z);
grid on;
st='\bf\fontname{times new roman}\fontsize{12} Функция отклика';
title(st);
xlabel('\bf\fontname{times new roman}\fontsize{12}  x'),
ylabel('\bf\fontname{times new roman}\fontsize{12}  y'),
zlabel('\bf  f(x,y)'),
zlim([0, 4])
disp('---------------------------------------------------')
fprintf('\t ПОСТАНОВКА  ДВУХФАКТОРНОГО  ЭКСПЕРИМЕНТА\n')
fprintf('\t Уравнение линейной модели:\n')
fprintf('\t f(x1,x2) = b0 + b1*x1 + b2*x2\n')
% ------ КРУТОЕ ВОСХОЖДЕНИЯ К ЭКСТРЕМУМУ ФУНКЦИИ ОТКЛИКА ------
fprintf('\n\t 1-й ЦИКЛ РАСЧЕТА\n')
% ОСНОВНОЙ УРОВЕНЬ ФАКТОРОВ
X10 = -0.3;
X20 = -1.5;
% РАСЧЕТ ФУНКЦИИ ОТКЛИКА В ЦЕНТРЕ НАЧАЛЬНОГО ПЛАНА
f0 = abs(pan1([X10,X20]));
% ИНТЕРВАЛЫ ВАРЬИРОВАНИЯ ФАКТОРОВ
d1 = -0.2;
d2 = -0.2;
% ЗНАЧЕНИЯ ФАКТОРОВ В ТОЧКАХ НАЧАЛЬНОГО ПЛАНА
X1up = X10 + d1;
X1dw = X10 - d1;
X2up = X20 + d2;
X2dw = X20 - d2;
% ВЫВОД СООБЩЕНИЙ
fprintf('\t Координаты центра начального плана:\n\t x10 = %g\n\t x20 = %g\n',X10,X20)
fprintf('\t Интервалы варьирования:\n\t Для 1-го фактора: %g\n\t Для 2-го фактора: %g\n', d1, d2)
fprintf('\t Значения отклика в точках начального плана:\n')
y0 = [abs(pan1([X1up,X2up])); abs(pan1([X1dw,X2up]));
    abs(pan1([X1up,X2dw]));  abs(pan1([X1dw,X2dw]))];
fprintf('\t\t %g\n',y0)
% ФОРМИРОВАНИЕ МАТРИЦЫ ПЛАНИРОВАНИЯ ФАКТОРОВ
fn = rot90(ff2n(2),2);
for J = 1:length(fn(:))
    if (~fn(J)) %%% когда fn(J) == 0
        fn(J) = -1;
    
else
        continue;
    end
end
X0 = [ones(length(fn(:,1)),1),fn];
%----------------------------------------------
fprintf('\tМатрица планирования двухфакторного эксперимента:\n')
fprintf('\t x0\t\t\tx1\t\t  x2\t\t y\n')
disp([X0,y0])
%----------------------------------------------
% РАСЧЕТ КОЭФФИЦИЕНТОВ ЛИНЕЙНОЙ МОДЕЛИ
b0 = regress(y0,X0);
fprintf('\t Коэффициенты линейной модели:\n')
for J = 1:length(b0) 
    fprintf('\t\t b%d = %g\n',J-1,b0(J))
end
%----------------------------------------------
fprintf('\t Значения градиента:\n')
for J = 2:length(b0)
    fprintf('\t g%d = %g\n',J-1,b0(J))
end
%----------------------------------------------
% ОРГАНИЗАЦИЯ ДВИЖЕНИЯ ПО ГРАДИЕНТУ
k = 0;
for J = 0.2:0.2:4
    k = k + 1;
aa(k) = J;
x11 = J*b0(2);
x22 = J*b0(3);
X1(k) = X10 + x11*d1;
X2(k) = X20 + x22*d2;
f1(k) = abs(pan1([X1(k),X2(k)]));
end
%-----------------------------------------------
k1 = find(f1 == max(f1));
% КООРДИНАТЫ ЦЕНТРА НОВОГО ПЛАНА
x10 = X1(k1);
x20 = X2(k1);
%-----------------------------------------------
fprintf('\t Число шагов поиска максимума функции отклика по направлению градиента: k = %d\n',k1)
fprintf('\t Параметр шага в направлении оценки градиента: a = %g\n',aa(k1))
fprintf('\t Расчетное значение функции отклика на градиенте: y1 = %g\n',max(f1))
fprintf('\t Координаты центра нового плана:\n\t x11 = %g\n\t x21 = %g\n',X1(k1),X2(k1))
disp('-------------------------------------------------')

fprintf('\t 2-й ЦИКЛ РАСЧЕТА\n')
% КООРДИНАТЫ ФАКТОРОВ НОВОГО ПЛАНА

X11up = x10 + d1;
X11dw = x10 - d1;
X21up = x20 + d2;
X21dw = x20 - d2;
%----------------------------------------------
fprintf('\t Новые интервалы варьирования:\n\t Для 1-го фактора: %g\n\t Для 2-го фактора: %g\n', d1, d2)
fprintf('\t Значения отклика в точках нового плана:\n')
y01 = [abs(pan1([X11up,X21up])); abs(pan1([X11dw,X21up]));
       abs(pan1([X11up,X21dw])); abs(pan1([X11dw,X21dw]))];
fprintf('\t\t %g\n',y01)
%----------------------------------------------
% ФОРМИРОВАНИЕ МАТРИЦЫ ПЛАНИРОВАНИЯ
fn = rot90(ff2n(2),2);
for J = 1:length(fn(:))
    if (~fn(J)) %% fn(J) == 0
        fn(J) = -1;
    else
        continue;
    end
end
X0 = [ones(length(fn(:,1)),1),fn];
%----------------------------------------------
fprintf('\tМатрица планирования двухфакторного эксперимента:\n')
fprintf('\t x0\t\t\tx1\t\t  x2\t\t y\n')
disp([X0,y01])

% РАСЧЕТ КОЭФФИЦИЕНТОВ ЛИНЕЙНОЙ МОДЕЛИ
b01 = regress(y01,X0);
fprintf('\t Коэффициенты линейной модели:\n')
for J = 1:length(b01) 
    fprintf('\t\t b%d = %g\n',J-1,b01(J))
end
%-----------------------------------------------
fprintf('\t Значения градиента:\n')
for J = 2:length(b01)
    fprintf('\t g%d = %g\n',J-1,b01(J))
end
%-----------------------------------------------
% ОРГАНИЗАЦИЯ ДВИЖЕНИЯ ПО ГРАДИЕНТУ
k = 0;
for J = 0.1:0.1:4
    k = k + 1;
aa(k) = J;
x11 = J*b01(2);
x22 = J*b01(3);
X11(k) = x10 + x11*d1;
X21(k) = x20 + x22*d2;
f11(k) = abs(pan1([X11(k),X21(k)]));
end
%----------------------------------------------

k1 = find(f11 == max(f11));
% КООРДИНАТЫ ЦЕНТРА НОВОГО ПЛАНА
x110 = X11(k1);
x220 = X21(k1);
%----------------------------------------------
fprintf('\t Число шагов поиска максимума функции отклика по направлению градиента: k = %d\n',k1)
fprintf('\t Параметр шага в направлении оценки градиента: a = %g\n',aa(k1))
fprintf('\t Расчетное значение функции отклика на градиенте: y2 = %g\n',max(f11))
fprintf('\t Координаты центра нового плана:\n\t x11 = %g\n\t x21 = %g\n',X11(k1),X21(k1))
disp('-------------------------------------------------')

fprintf('\t 3-й ЦИКЛ РАСЧЕТА\n')
% КООРДИНАТЫ ФАКТОРОВ НОВОГО ПЛАНА
X11up = x110 + d1;
X11dw = x110 - d1;
X21up = x220 + d2;
X21dw = x220 - d2;
%----------------------------------------------
fprintf('\t Новые интервалы варьирования:\n\t Для 1-го фактора: %g\n\t Для 2-го фактора: %g\n', d1, d2)
fprintf('\t Значения отклика в точках нового плана:\n')
y03 = [abs(pan1([X11up,X21up])); abs(pan1([X11dw,X21up]));
       abs(pan1([X11up,X21dw])); abs(pan1([X11dw,X21dw]))];
fprintf('\t\t %g\n',y01)
%----------------------------------------------
% ФОРМИРОВАНИЕ МАТРИЦЫ ПЛАНИРОВАНИЯ
fn = rot90(ff2n(2),2);
for J = 1:length(fn(:))
    if (~fn(J)) %% fn(J) == 0
        fn(J) = -1;
    else
        continue;
    end
end
X0 = [ones(length(fn(:,1)),1),fn];
%---------------------------------------------
fprintf('\tМатрица планирования двухфакторного эксперимента:\n')
fprintf('\t x0\t\t\tx1\t\t  x2\t\t y\n')
disp([X0,y03])
%---------------------------------------------
% РАСЧЕТ КОЭФФИЦИЕНТОВ ЛИНЕЙНОЙ МОДЕЛИ
b03 = regress(y03,X0);
fprintf('\t Коэффициенты линейной модели:\n')
for J = 1:length(b03) 
    fprintf('\t\t b%d = %g\n',J-1,b03(J))
end
%---------------------------------------------

fprintf('\t Значения градиента:\n')
for J = 2:length(b03)
    fprintf('\t g%d = %g\n',J-1,b03(J))
end
%----------------------------------------------
% ОРГАНИЗАЦИЯ ДВИЖЕНИЯ ПО ГРАДИЕНТУ
k = 0;
for J = 0.2:0.2:2
    k = k + 1;
aa(k) = J;
x11 = J*b03(2);
x22 = J*b03(3);
X11(k) = x110 + x11*d1;
X21(k) = x220 + x22*d2;
f33(k) = abs(pan1([X11(k),X21(k)]));
end
%-----------------------------------------------
k3 = find(f33 == max(f33));
% КООРДИНАТЫ ЦЕНТРА НОВОГО ПЛАНА
x110 = X11(k3);
x220 = X21(k3);
%------------------------------------------------
fprintf('\t Число шагов поиска максимума функции отклика по направлению градиента: k = %d\n',k3)
fprintf('\t Параметр шага в направлении оценки градиента: a = %g\n',aa(k3))
fprintf('\t Расчетное значение функции отклика на градиенте: y3 = %g\n',max(f33))
fprintf('\t Координаты центра нового плана:\n\t x11 = %g\n\t x21 = %g\n',X11(k3),X21(k3))
disp('-------------------------------------')

fprintf('\t 4-й ЦИКЛ РАСЧЕТА\n')
% ИНТЕРВАЛЫ ВАРЬИРОВАНИЯ ФАКТОРОВ
d41 = -0.1; d42 = -0.1;
% КООРДИНАТЫ ФАКТОРОВ НОВОГО ПЛАНА
X11up = x110 + d41;
X11dw = x110 - d41;
X21up = x220 + d42;
X21dw = x220 - d42;
%-------------------------------------------

fprintf('\t Новые интервалы варьирования\n\t Для 1-го фактора: %g\n\t Для 2-го фактора: %g\n', d41, d42)
fprintf('\t Значения отклика в точках нового плана:\n')
y04 = [abs(pan1([X11up,X21up])); abs(pan1([X11dw,X21up]));
       abs(pan1([X11up,X21dw])); abs(pan1([X11dw,X21dw]))];
fprintf('\t\t %g\n', y04)

% ФОРМИРОВАНИЕ МАТРИЦЫ ПЛАНИРОВАНИЯ
fn = rot90(ff2n(2), 2);

for J = 1:length(fn(:))
    if (~fn(J))   %% когда fn(J) == 0
        fn(J) = -1;
    else
        continue;
    end
end
X0 = [ones(length(fn(:,1)),1), fn];
%---------------------------------------------
fprintf('\tМатрица планирования двухфакторного эксперимента:\n')
fprintf('\t x0\t\t\tx1\t\t  x2\t\t y\n')
disp([X0, y04])
%----------------------------------------------
% РАСЧЕТ КОЭФФИЦИЕНТОВ ЛИНЕЙНОЙ МОДЕЛИ
b04 = regress(y04,X0);
fprintf('\t Коэффициенты линейной модели:\n')
for J = 1:length(b04) 
    fprintf('\t\t b%d = %g\n', J-1, b04(J))
end
fprintf('\t Значения градиента:\n')
for J = 2:length(b04)
    fprintf('\t g%d = %g\n', J-1, b04(J))
end
%----------------------------------------------
% ОРГАНИЗАЦИЯ ДВИЖЕНИЯ ПО ГРАДИЕНТУ
k = 0;
for J = 5:0.5:10
    k = k + 1;
aa(k) = J;
x11 = J*b04(2);
x22 = J*b04(3);
X11(k) = x110 + x11*d41;
X21(k) = x220 + x22*d42;
f44(k) = abs(pan1([X11(k), X21(k)]));
end
%-------------------------------------------------
k4 = find(f44 == max(f44));
% КООРДИНАТЫ ЦЕНТРА НОВОГО ПЛАНА
x110 = X11(k4);
x220 = X21(k4);
%-------------------------------------------------

fprintf('\t Число шагов поиска максимума функции отклика по направлению градиента: k = %d\n', k4)
fprintf('\t Параметр шага в направлении оценки градиента: a = %g\n',aa(k4))
fprintf('\t Расчетное значение функции отклика на градиенте: y4 = %g\n',max(f44))
fprintf('\t Координаты центра нового плана:\n\t x11 = %g\n\t x21 = %g\n',X11(k4),X21(k4))
disp('-----------------------------------------------')
 
function f = pan1(w)
%%% М-файл описания заданной функции
%%% двух переменных
x = w(1);
y = w(2);
f = 3*(1-x)^2*exp(-x^2-(y+1)^2);

Результат выполнения программы

Аналитический вид функции отклика:
	 f(x,y) = 3*(1-x)^2*exp(-x^2-(y+1)^2)
	 Оптимальные значения факторов:
	 x_optim = -0.618038
	 y_optim = -0.999985
	 Значение макcимума аналитической функции отклика:
	 f(x,y)_max = 5.36057
--------------------------------------------------------------
	 ПОСТАНОВКА  ДВУХФАКТОРНОГО  ЭКСПЕРИМЕНТА
	 Уравнение линейной модели:
	 f(x1,x2) = b0 + b1*x1 + b2*x2
	 1-й ЦИКЛ РАСЧЕТА
	 Координаты центра начального плана:
	 x10 = -0.3
	 x20 = -1.5
	 Интервалы варьирования:
	 Для 1-го фактора: -0.2
	 Для 2-го фактора: -0.2
	 Значения отклика в точках начального плана:
		 3.22052
		 2.20171
		 4.80445
		 3.28456
	Матрица планирования двухфакторного эксперимента:
      x0		x1	     x2		 y
    1.0000    1.0000    1.0000    3.2205
    1.0000   -1.0000    1.0000    2.2017
    1.0000    1.0000   -1.0000    4.8044
    1.0000   -1.0000   -1.0000    3.2846
	 Коэффициенты линейной модели:
		 b0 = 3.37781
		 b1 = 0.634676
		 b2 = -0.666696
	 Значения градиента:
	 g1 = 0.634676
	 g2 = -0.666696
Число шагов поиска максимума функции отклика по направлению градиента: k = 15
	 Параметр шага в направлении оценки градиента: a = 3
	 Расчетное значение функции отклика на градиенте: y1 = 5.27863
	 Координаты центра нового плана:
	 x11 = -0.680805
	 x21 = -1.09998
---------------------------------------------------------------
	 2-й ЦИКЛ РАСЧЕТА
	 Новые интервалы варьирования:
	 Для 1-го фактора: -0.2
	 Для 2-го фактора: -0.2
	 Значения отклика в точках нового плана:
		 4.46471
		 4.77131
		 4.8365
		 5.16863
	Матрица планирования двухфакторного эксперимента:
     x0	       x1	     x2		 y
    1.0000    1.0000    1.0000    4.4647
    1.0000   -1.0000    1.0000    4.7713
    1.0000    1.0000   -1.0000    4.8365
    1.0000   -1.0000   -1.0000    5.1686
	 
      Коэффициенты линейной модели:
		 b0 = 4.81029
		 b1 = -0.159682
		 b2 = -0.192275
	 
     Значения градиента:
	 g1 = -0.159682
	 g2 = -0.192275
Число шагов поиска максимума функции отклика по направлению градиента: k = 23
	 Параметр шага в направлении оценки градиента: a = 2.3
	 Расчетное значение функции отклика на градиенте: y2 = 5.35901
	 Координаты центра нового плана:
	 x11 = -0.607352
	 x21 = -1.01154
-----------------------------------------------------------------
	 3-й ЦИКЛ РАСЧЕТА
	 Новые интервалы варьирования:
	 Для 1-го фактора: -0.2
	 Для 2-го фактора: -0.2
	 Значения отклика в точках нового плана:
		 4.46471
		 4.77131
		 4.8365
		 5.16863
	Матрица планирования двухфакторного эксперимента:
      x0	      x1         x2		 y
    1.0000    1.0000    1.0000    4.8831
    1.0000   -1.0000    1.0000    4.8131
    1.0000    1.0000   -1.0000    4.9283
    1.0000   -1.0000   -1.0000    4.8578
	 Коэффициенты линейной модели:
		 b0 = 4.87058
		 b1 = 0.0351275
		 b2 = -0.0224743
	 

     Значения градиента:
	 g1 = 0.0351275
	 g2 = -0.0224743
Число шагов поиска максимума функции отклика по направлению градиента: k = 9
	 Параметр шага в направлении оценки градиента: a = 1.8
	 Расчетное значение функции отклика на градиенте: y3 = 5.36048
	 Координаты центра нового плана:
	 x11 = -0.619997
	 x21 = -1.00345
-----------------------------------------------------------------
	 4-й ЦИКЛ РАСЧЕТА
	 Новые интервалы варьирования:
	 Для 1-го фактора: -0.1
	 Для 2-го фактора: -0.1
	 
      Значения отклика в точках нового плана:
		 5.22869
		 5.23272
		 5.2359
		 5.23994
	
   Матрица планирования двухфакторного эксперимента:
      x0 	      x1         x2		 y
    1.0000    1.0000    1.0000    5.2287
    1.0000   -1.0000    1.0000    5.2327
    1.0000    1.0000   -1.0000    5.2359
    1.0000   -1.0000   -1.0000    5.2399
	 Коэффициенты линейной модели:
		 b0 = 5.23431
		 b1 = -0.002017
		 b2 = -0.00360653
	 Значения градиента:
	 g1 = -0.002017
	 g2 = -0.00360653
Число шагов поиска максимума функции отклика по направлению градиента: k = 10
	 Параметр шага в направлении оценки градиента: a = 9.5
	 Расчетное значение функции отклика на градиенте: y4 = 5.36057
	 Координаты центра нового плана:
	 x11 = -0.618081
	 x21 = -1.00002
-----------------------------------------------------------------

Задание

На поверхности функции отклика вычертите линии движения к экстремуму.
Выведите значения функции отклика в точках оптимального плана, когда в центре его достигается оценка максимума функции отклика.
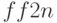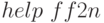Примените функцию (см. $help\mbox{ }ff2n$ ) без перестановки столбцов, которая в программе выполнялпсь с помощью . Проанализируйте полученные результаты.
Измените координаты начального плана: удалите их от оптимума, установите в непосредственной близости к экстремуму функции отклика.
Напишите программу поиска максимума функции отклика с автоматическим выбором количества циклов, значений шага по градиенту, с заданием в диалоговых окнах интервалов варьирования и центра начального плана.

Контрольные вопросы

Что такое функция отклика?
В чем различие между пассивным и активным экспериментами?
Какие задачи решает активный эксперимент?
Что называется градиентом функции отклика?
В чем заключается методика поиска экстремума функции отклика?
Почему используются линейные модели при поиске экстремума функции отклика?
Как осуществляется построение факторного эксперимента в окрестности заданной точки факторного пространства?
На каком этапе поиска экстремума функции отклика применяется метод наименьших квадратов?

Дальше >>

Авторизоваться

Моделирование систем

Планирование активного эксперимента при поиске оптимальных условий

Практическая часть

Контрольные вопросы

Вопросы и ответы