|
Добрый день. Я приступила сегодня к самостоятельному изучению курса "Моделирование систем". Хочу понять - необходимо ли отсылать мои решения практических заданий на сайт, (и если да - то где найти волшебную кнопку "Загрузить...") или практические задания остаются полностью на моей совести? (никто не проверяет, и отчётности по ним я предоставлять не обязана?) P.S.: тьютора я не брала |
Моделирование многоканальных систем массового обслуживания
2.3. Пример моделирования системы типа М/М/M/K/M
Система 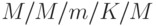 — это система с пуассоновским входящим пото-ком требований, с экспоненциальным законом обслуживания в m приборах, с допустимым числом требований в системе, не превышающим K, и с ограниченным числом источников нагрузки, которые создают поток из
— это система с пуассоновским входящим пото-ком требований, с экспоненциальным законом обслуживания в m приборах, с допустимым числом требований в системе, не превышающим K, и с ограниченным числом источников нагрузки, которые создают поток из  требований. Общее число K требований в системе заключено в интервале
требований. Общее число K требований в системе заключено в интервале 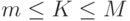 , где
, где  — число требований, формируемых конечным числом источников нагрузки.
— число требований, формируемых конечным числом источников нагрузки.
Предполагается, что требования, поступающие в систему, когда в ней уже имеется  требований, теряются и немедленно возвращаются в группу поступающих так, как будто бы они полностью обслужены. Для описанного функционирования системы и ее заданного буквенного обозначения можно определить ее параметры в соответствии с процессом размножения и гибели в следующем виде:
требований, теряются и немедленно возвращаются в группу поступающих так, как будто бы они полностью обслужены. Для описанного функционирования системы и ее заданного буквенного обозначения можно определить ее параметры в соответствии с процессом размножения и гибели в следующем виде:

Диаграмма интенсивностей переходов для системы 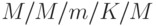 будет представлять собой конечный размеченный граф состояний, который показан на рис. 2.5.
будет представлять собой конечный размеченный граф состояний, который показан на рис. 2.5.
На рис. 2.5 вертикальными штриховыми линиями размечены границы между состояниями системы, с помощью которых можно найти стационарные вероятности состояний по следующему мнемоническому правилу: на границе раздела двух состояний размеченного графа поток вероятности слева от границы равен потоку вероятности справа от границы.
Для определения дифференциальных уравнений относительно вероятностей состояний следует каждое состояние описать воображаемой окружностью и далее применить мнемоническое правило составления дифференциальных уравнений Колмогорова: производная вероятности любого состояния равна сумме потоков вероятности, переводящих систему в это состояние, минус сумма всех потоков вероятности, выводящих систему из этого состояния [4].
Запишем следующее выражение для определения стационарных вероятностей состояний от  до
до 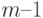 :
:
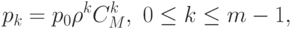
где:
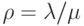 ,
,
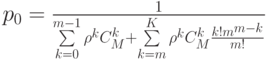 — вероятность нулевого состояния.
— вероятность нулевого состояния.
Расчет вероятностей состояний от  до
до  :
:
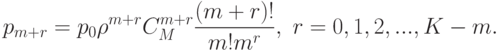
Если в последнем выражении сделать замену 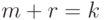 ,
, 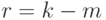 , то получим
, то получим
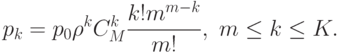
Вероятность нулевого состояния была определена из нормировочного условия:
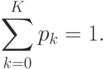
Рассмотрим случай, когда система 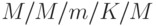 работает в режиме чистых потерь, т. е. когда параметры системы удовлетворяют условию
работает в режиме чистых потерь, т. е. когда параметры системы удовлетворяют условию 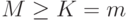 . Расчет вероятностей состояний будет определяться при
. Расчет вероятностей состояний будет определяться при  :
:
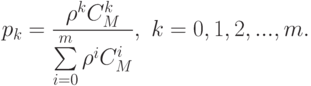
Распределение вероятностей в соответствии с последней формулой называется распределением Энгсета .
В соответствии с размеченным графом состояний и с помощью мнемонического правила составим следующие дифференциальные уравнения относительно вероятностей состояний системы:
![\frac{dP_{0}}{dt}=-M\lambda P_{0}+\mu P_{1};\\
\frac{dP_{1}}{dt}=M\lambda P_{0}-[(M-1)\lambda +\mu] P_{1}+2\mu P_{2};\\
\frac{dP_{2}}{dt}=(M-1)\lambda P_{1}-[(M-2)\lambda +2\mu] P_{2}+3\mu P_{3};\\
.............................\\
\frac{dP_{m}}{dt}=[M-(m-1)]\lambda P_{m-1}-[(M-m)\lambda +m\mu] P_{m}+m\mu P_{m+1};\\
.............................\\
\frac{dP_{K-1}}{dt}=[M-(K-2)]\lambda P_{K-2}-\{[M-(KI-1)]\lambda +m\mu\} P_{K-1}+m\mu P_{K};\\
\frac{dP_{K}}{dt}=[M-(K-1)]\lambda P_{K-1}-m\mu P_{K}.](/sites/default/files/tex_cache/7e1d2939e047849296f11693e886b71b.png)
Для решения дифференциальных уравнений следует задать начальные условия. Обычно используются естественные начальные условия, т. е.

Для стационарного режима рассмотрим ряд операционных характеристик в достаточно общем виде.
Среднее число требований в системе:
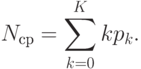
Среднее время пребывания одного требования в системе определим по формуле Литтла:
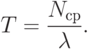
Средняя длина очереди:
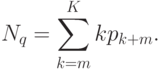
Среднее время пребывания требования в очереди определим по формуле Литтла:

Вероятность отказа в обслуживании соответствует вероятности того, что в системе находится  требований (максимально допустимое число):
требований (максимально допустимое число):
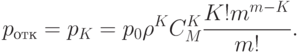
Относительная пропускная способность:
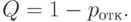
Абсолютная пропускная способность:
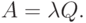
Таким образом, операционные характеристики рассчитываются по известным стационарным вероятностям и параметрам системы.


 —
—