|
приветствую создателей курса и благодарю за доступ к информации! понимаю, что это уже никто не исправит, но, возможно, будут следующие версии и было бы неплохо дать расшифровку сокращений имен регистров итд, дабы закрепить понимание их роли в общем процессе. |
Процессоры цифровой обработки сигналов
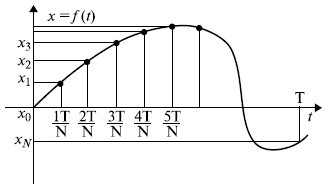
Рассмотрим теперь функцию x = f(t), представляющую собой некоторое звуковое или какое-либо иное колебание. Пусть это колебание описано графиком на временном интервале [0, T] (рис. 16.2).
Для обработки этого сигнала в компьютере нужно выполнить его дискретизацию. С этой целью временной интервал делится на N-1 частей
и сохраняются значения функции x0, x1, x2, ..., xN-1 для N точек на границах интервалов.
В результате прямого дискретного преобразования Фурье могут быть получены N значений для Xk согласно (16.1).
Если теперь применить обратное дискретное преобразование Фурье, то получится исходная последовательность {xn}. Исходная последовательность состояла из действительных чисел, а последовательность {Xk} в общем случае комплексная. Если приравнять нулю ее мнимую часть, то получим:
![x_n=f(t_n)=\sum_{k=0}^{N-1}[\frac{Re_{k}}{N}\cos{(\frac{2\pi{k}n}{N})}-\frac{Im_k}{N}\sin{(\frac{2\pi{k}n}{N})}]+
\sum_{k=0}^{N-1}[\frac{Re_{k}}{N}\cos{(\frac{2\pi{k}_{n}}{N})}-\frac{Im_k}{N}
\sin{(\frac{2\pi{k}_{n}}{N})}]](/sites/default/files/tex_cache/c9be34eddfff27f345319bfebbe4bc0d.png) |
( 16.8) |
Сопоставив эту формулу с формулами (16.4) и (16.6) для гармоники, увидим, что выражение (16.8) представляет собой сумму из N гармонических колебаний разной частоты, фазы и амплитуды. То есть физический смысл дискретного преобразования Фурье состоит в том, чтобы представить некоторый дискретный сигнал в виде суммы гармоник. Параметры каждой гармоники вычисляются прямым преобразованием Фурье, а сумма гармоник - обратным.
Теперь, например, операция "фильтр нижних частот", которая "вырезает" из сигнала все частоты выше некоторой заданной, может просто обнулить коэффициенты, соответствующие частотам, которые необходимо удалить. Затем, после обработки, выполняется обратное преобразование.
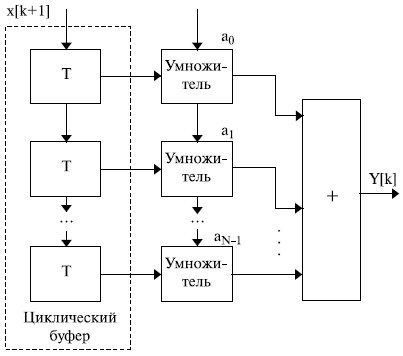
Особенности цифровой обработки сигналов рассмотрим на примере алгоритма нерекурсивной фильтрации. Структура устройства, реализующего данный алгоритм, показана на рис. 16.3.
Обработка заключается в формировании выходного сигнала Y[k] по значениям N последних входных отсчетов x[k], которые поступают на вход устройства через определенный интервал времени Т. Принятые отсчеты сохраняются в ячейках циклического буфера. При приеме очередного отсчета содержимое всех ячеек буфера переписывается в соседнюю позицию, самый старый отсчет покидает буфер, а новый записывается в его младшую ячейку.
Аналитически алгоритм работы нерекурсивного фильтра записывается как:
![Y[k]=\sum_{i=1}^{N-1}x[k-1]*a_i](/sites/default/files/tex_cache/7bb24ab792cd2c4360f3aa8f0322d2de.png) |
( 16.9) |
где ai - коэффициенты, определяемые типом фильтра.
Отсчеты с выходов элементов буфера поступают на умножители, на вторые входы которых поступают коэффициенты ai. Результаты произведений складываются и формируют отсчет выходного сигнала Y[k], после чего содержимое буфера сдвигается на 1 позицию и цикл работы фильтра повторяется. Выходной сигнал Y[k] должен быть вычислен до поступления следующего входного сигнала, то есть за интервал T. В этом заключается суть работы устройства в реальном масштабе времени. Интервал времени T задается частотой дискретизации, которая определяется областью применения фильтра. По следствию из теоремы Котельникова в дискретном сигнале период, соответствующий наивысшей представимой частоте, соответствует двум периодам дискретизации. При обработке звукового сигнала частоту дискретизации можно принять в 40 кГц. В этом случае если необходимо реализовать цифровой нерекурсивный фильтр 50-го порядка, то за время в 1/40 кГц = 25 мкс должно быть выполнено 50 умножений и 50 накоплений результатов умножения. Для обработки видеосигнала интервал времени, за который должны быть выполнены эти действия, будет на несколько порядков меньше.
Если выполнять ДПФ входной последовательности напрямую, строго по исходной формуле, то потребуется много времени. Посчитав по определению ( N раз суммировать N слагаемых), получаем величину порядка N2.
Тем не менее, можно обойтись существенно меньшим числом операций.
Наиболее популярным из алгоритмов ускоренного вычисления ДПФ является метод Кули-Тьюки (Cooley-Tukey), позволяющий вычислить ДПФ для числа отсчетов N = 2k за время порядка N*log2 N (отсюда и название - быстрое преобразование Фурье, БПФ, или в английском варианте FFT - Fast Fourier TRansformation ). Основная идея этого метода заключается в рекурсивном разбиении массива чисел на два подмассива и сведении вычисления ДПФ от целого массива к вычислению ДПФ от подмассивов в отдельности. При этом процесс разбиения исходного массива на подмассивы проводится по методу побитовой обратной сортировки ( bit-reversal sortINg ).
Сначала входной массив делится на две подмассива - с четными и нечетными номерами. Каждый из подмассивов перенумеровывается и снова делится на два подмассива - с четными и нечетными номерами. Эта сортировка продолжается до тех пор, пока размер каждого подмассива не достигнет 2 элементов. В результате (что можно показать математически) номер каждого исходного элемента в двоичной системе переворачивается. То есть, например, для однобайтных номеров двоичный номер 00000011 станет номером 110000000, номер 01010101 - номером 10101010.
Существуют алгоритмы БПФ для случаев, когда N является степенью произвольного простого числа (а не только двойки), а также в случае, когда число N является произведением степеней простых чисел любого числа отсчетов. Однако БПФ, реализованное по методу Кули-Тьюки для случая N = 2k, получило наиболее широкое распространение. Причина этого в том, что алгоритм, построенный по этому методу, обладает рядом очень хороших технологических свойств:
- структура алгоритма и его базовые операции не зависят от числа отсчетов (меняется только число прогонов базовой операции);
- алгоритм легко распараллеливается с использованием базовой операции и конвейеризуется, а также легко каскадируется (коэффициенты БПФ для 2N отсчетов могут быть получены преобразованием коэффициентов двух БПФ по N отсчетов, полученных "прореживанием" исходных 2N отсчетов через один);
- алгоритм прост и компактен, допускает обработку данных "на месте" и не требует дополнительной оперативной памяти.
Однокристальные микроконтроллеры и даже универсальные микропроцессоры оказываются относительно медленными при выполнении операций, характерных для ЦОС. К тому же требования к качеству преобразования аналоговых сигналов постоянно возрастают. В сигнальных микропроцессорах такие операции поддерживаются на аппаратном уровне и выполняются, соответственно, достаточно быстро. Работа в реальном масштабе времени требует от процессора также поддержки на аппаратном уровне таких действий, как обработка прерываний, программных циклов.
Все это приводит к тому, что DS P-процессоры, архитектурно включая в себя многие черты как универсальных микропроцессоров, особенно с RISC-архитектурой, так и однокристальных микроконтроллеров, в то же время значительно отличаются от них. Универсальный микропроцессор помимо чисто вычислительных операций выполняет функцию объединяющего звена всей микропроцессорной системы, в частности компьютера.
Он должен управлять работой различных компонентов аппаратного обеспечения, таких как дисководы, графические дисплеи, сетевой интерфейс, с тем чтобы обеспечить их согласованную работу. Это приводит к достаточно сложной архитектуре, поскольку она должна поддерживать наряду с целочисленной арифметикой и операциями с плавающей запятой такие базовые функции, как защита памяти, мультипрограммирование, обработка векторной графики и т. п. В итоге типичный универсальный микропроцессор с CISC-, а зачастую и RISC-архитектурой имеет систему из несколько сотен команд, которые обеспечивают выполнение всех этих функций, и соответствующую аппаратную поддержку. Это ведет к необходимости иметь в составе такого МП десятки миллионов транзисторов.
В то же время DSP-процессор является узкоспециализированным устройством. Его единственная задача - быстро обрабатывать поток цифровых сигналов. Он состоит главным образом из высокоскоростных аппаратных схем, выполняющих арифметические функции и манипулирующих битами, оптимизированных таким образом, чтобы быстро обрабатывать большие объемы данных. В силу этого набор команд у DSP куда меньше, чем у универсального микропроцессора: их число обычно не превышает 80. Это значит, что для DSP требуется облегченный декодер команд и гораздо меньшее число исполнительных устройств. Кроме того, все исполнительные устройства в конечном итоге должны поддерживать высокопроизводительные арифметические операции. Таким образом, типичный DSP-процессор состоит не более чем из нескольких сот тысяч (а не десятков миллионов, как в современных CISC-МП) транзисторов. В силу этого такие МП потребляют меньше энергии, что позволяет использовать их в продуктах, работающих от батарей. Крайне упрощается их производство, поэтому они находят себе применение в недорогих устройствах. Сочетание низкого энергопотребления и невысокой стоимости позволяет использовать их не только в высокой сфере телекоммуникаций, но и в сотовых телефонах и роботах-игрушках.
Отметим основные особенности архитектуры процессоров цифровой обработки сигналов:
- Гарвардская архитектура, основу которой составляет физическое и логическое разделение памяти команд и памяти данных. Ключевые команды DSP-процессора являются многооперандными, и ускорение их работы требует одновременного чтения нескольких ячеек памяти. Соответственно на кристалле имеются раздельные шины адреса и данных (в некоторых типах процессоров - несколько шин адреса и данных). Это позволяет совмещать во времени выборку операндов и исполнение команд. Использование модифицированной гарвардской архитектуры предполагает, что операнды могут храниться не только в памяти данных, но и в памяти команд вместе с программами. Например, в случае реализации цифровых фильтров коэффициенты могут храниться в памяти программ, а значения данных - в памяти данных. Поэтому коэффициент и данные могут выбираться в одном машинном цикле. Для обеспечения выборки команды в том же машинном цикле используется либо кэш-память программ, либо двукратное обращение к памяти программ за время машинного цикла.
- Для сокращения времени выполнения одной из основных операций цифровой обработки сигнала - умножения - применяется аппаратный умножитель. В процессорах общего назначения эта операция реализуется за несколько тактов сдвига и сложения и занимает много времени, а в DSP-процессорах благодаря специализированному умножителю нужен всего один цикл. Встроенная схема аппаратного умножения позволяет выполнить за 1 такт основную операцию ЦОС - умножение с накоплением ( MultIPly-Accumulate - MAC ) для 16- и/или 32-разрядных операндов.
- Аппаратная поддержка циклических буферов. Например, для фильтра, представленного на рис. 16.3, при каждом вычислении отсчета выходного сигнала используется новый отсчет входного сигнала, который сохраняется в памяти на месте самого старого. Для такого циркулирующего буфера может использоваться фиксированная область ОЗУ. При этом во время вычислений генерируются лишь последовательные значения адресов ОЗУ вне зависимости от того, какая операция - запись или чтение - выполняется в настоящий момент. Аппаратная реализация циклических буферов позволяет установить параметры буфера (адрес начала, длина) в программе вне тела цикла фильтрации, что позволяет сократить время выполнения циклического участка программы.
- Сокращение длительности командного такта. Это во многом обеспечивается приемами, характерными для RISC-процессоров. Главными из них являются размещение операндов большинства команд в регистрах, а также конвейеризация на уровне команд и микрокоманд. Конвейер имеет от 2 до 10 ступеней, что позволяет на различных стадиях выполнения одновременно обрабатывать до 10 команд. При этом используется генерация адресов регистров параллельно с выполнением арифметических операций, а также многопортовый доступ к памяти. Сюда же можно отнести и такой прием, характерный для универсальных микропроцессоров с EPIC-архитектурой, как применение команд со сверхбольшой длиной слова (VLIW), генерируемых на стадии компиляции программы. Этому же служит и рассмотренная выше гарвардская архитектура процессора, характерная для однокристальных микроконтроллеров.
- Наличие на кристалле процессора внутренней памяти, что роднит ЦСП с однокристальными МК. Встроенная в процессор память обычно имеет значительно большее быстродействие, чем внешняя. Наличие встроенной памяти позволяет значительно упростить систему в целом, уменьшить ее размеры, энергопотребление и стоимость. Емкость внутренней памяти является результатом определенного компромисса. Ее увеличение ведет к удорожанию процессора и увеличивает энергопотребление, а ограниченная емкость памяти программ не позволяет хранить сложные алгоритмы. Большинство DS P-процессоров с фиксированной точкой имеют малую емкость внутренней памяти, обычно от 4 до 256 Кбайт, и невысокую разрядность внешних шин данных, связывающих процессор с внешней памятью. В то же время ЦСП с плавающей точкой обычно предполагают работу с большими массивами данных и сложными алгоритмами и имеют либо встроенную память большой емкости, либо большую разрядность адресных шин для подключения внешней памяти (а иногда и то, и другое).
- Широкие возможности по аппаратному взаимодействию с внешними устройствами, включающие:
- большое разнообразие интерфейсов, в том числе контроллеры локальной промышленной сети CAN, встроенные коммуникационные (SCI) и периферийные (SPI) интерфейсы, I2C, UART;
- несколько входов для аналоговых сигналов и, соответственно, встроенный АЦП;
- выходные каналы широтно-импульсной модуляции (ШИМ);
- развитую систему внешних прерываний;
- контроллеры прямого доступа в память.
- В некоторых DSP-семействах предусмотрены специальные аппаратные средства, облегчающие создание мультипроцессорных систем с параллельной обработкой данных для наращивания производительности.
- DSP-процессоры широко используются в мобильных устройствах, где потребляемая мощность является основной характеристикой. Для снижения энергопотребления в сигнальных процессорах применяется множество методов, в том числе уменьшение напряжения питания и введение функций управления потреблением, например, динамическое изменение тактовой частоты, переключение в спящий или дежурный режим либо отключение не используемой в данный момент периферии. Следует отметить, что эти меры оказывают значительное воздействие на скорость работы процессора и при некорректном использовании могут привести к неработоспособности проектируемого устройства (в качестве примера можно упомянуть некоторые сотовые телефоны, которые в результате ошибок в программах управления энергопотреблением иногда переставали включаться) или к ухудшению его эксплуатационных характеристик (например, значительному времени восстановления работоспособности при выходе из спящего режима).
Система команд сигнальных процессоров имеет многие черты систем команд универсальных микропроцессоров (особенно с RISC-архитектурой) и однокристальных микроконтроллеров. Она включает в себя основные арифметические и логические операции и команды переходов, но в меньшем, чем в универсальных МП, количестве. Число режимов адресации операндов также относительно невелико. Команда имеет простой, четко заданный формат. Длина команды составляет одно, реже два 16-разрядных слова. Однако наряду с использованием сокращенного набора команд, в DSP-процессорах применяются и такие характерные для MMX-обработки аппаратно поддерживаемые инструкции, как команды поиска минимума и максимума, получения абсолютного значения, сложения с насыщением, при котором в случае переполнения при сложении двух чисел результату присваивается максимально возможное в данной разрядной сетке значение. Это ведет к уменьшению количества конфликтов в конвейере и повышает эффективность работы процессора.
С другой стороны, ЦСП содержат ряд команд, наличие которых обусловлено спецификой их применения и которые вследствие этого редко присутствуют в микропроцессорах других типов. Прежде всего это, конечно, команда умножения с накоплением суммы MAC, лежащая в основе ЦОС: А = В*С+А. В системах команд некоторых сигнальных процессоров можно при программировании указать число выполнений этой команды в цикле и правила изменения индексов для адресации операндов В и С. При этом в отличие от команд повторения обычных процессоров сигнальный процессор может аппаратно поддерживать проверку условия завершения цикла. Сюда же можно отнести и команды сдвига (перезаписи) в соседнюю ячейку ОЗУ данных, поддерживающие работу циклического буфера для подготовки умножения в следующем такте.
Для эффективной реализации алгоритмов БПФ в систему команд некоторых DSP-процессоров включены возможности адресации с реверсированием бит адреса.
Программирование микропроцессоров этого класса также имеет свои особенности. Значительное удобство для разработчика, обычно связываемое с использованием языков высокого уровня, в большинстве случаев оборачивается получением менее компактного и быстрого кода. Так как особенности ЦОС предполагают работу в реальном времени, это приводит к необходимости использования для решения тех же задач более мощных и дорогих DSP. Такая ситуация особенно критична для крупносерийной продукции, где разница в стоимости более производительного DSP или дополнительного процессора играет важную роль. В то же время в современных условиях скорость разработки (и, следовательно, выхода нового изделия на рынок) может принести больше выгод, чем затраты времени на оптимизацию кода при написании программы на ассемблере.
Компромиссным подходом здесь служит использование ассемблера для написания наиболее критичных с точки зрения время- и ресурсоемкости участков программы, в то время как основная часть программы пишется на языке высокого уровня, как правило, Си или Си++.