Целостность сообщения и установление подлинности сообщения

1.4. Рекомендованная литература

Для более детального изучения положений, обсужденных в этой лекции, мы рекомендуем нижеследующие книги и сайты. Пункты, указанные в скобках, показаны в списке ссылок в конце книги.

Книги

Книги [Sti06], [Sta06], [Sch99], [Mao04], [KPS02], [PHS03L] и [MOV97] дают хороший обзор криптографических хэш-функций.

Сайты

Нижеследующие сайты содержат больше информации о темах, рассмотренных в этой лекции.

• http://en.wikipedia.org/wiki/Preimage_attack
• http://en.wikipedia.org/wiki/Collision_attack#In_cryptography
• http://en.wikipedia.org/wiki/Pigeonhole __ principle
• csrc.nist.gov/ispab/2005-12/B_Burr-Dec2005-ISPAB.pdf
• http://en.wikipedia.org/wiki/Message_authentication_code
• http://en.wikipedia.org/wiki/HMAC
• csrc.nist.gov/pLiblicationVnps/npsl98/fips-198a.pdf
• http://www.faqs.org/rfcs rfc2104.html
• http://en.wikipedia.org/wiki/Birthday_paradox

1.5. Итоги

• Отпечаток пальца или дайджест сообщения могут использоваться для того, чтобы гарантировать целостность документа или сообщения. Чтобы гарантировать целостность документа, необходимы документ и отпечаток пальца; чтобы гарантировать целостность сообщения, необходимы сообщение и дайджест сообщения. Дайджест сообщения надо оберегать от изменения.
• Криптографическая хэш-функция создает дайджест сообщения из сообщения. Функция должна соответствовать трем критериям: устойчивость к прообразу, устойчивость ко второму прообразу и устойчивость к коллизиям.
• Первый критерий - устойчивость к прообразу - означает, что для Евы должно быть чрезвычайно трудно создать любое сообщение, соответствующее этому дайджесту. Второй критерий - устойчивость второго прообраза - гарантирует, что если Ева имеет сообщение и соответствующий дайджест, она не сможет создать второе сообщение, дайджест которого тот же самый, что и у первого. Третий критерий - устойчивость к коллизиям - гарантирует, что Ева не может найти два сообщения, которые хэшируются и приводят к одному и тому же дайджесту.
• Случайная модель Oracle, которая была введена в 1993 г. Белларом и Роджеем, является идеальной математической моделью для хэш-функции.
• Принцип голубиных ящиков устанавливает, что если n ящиков заняты n + 1 голубем, то по крайней мере один ящик занят двумя голубями. Обобщенная версия принципа голубиных ящиков: если n ящики заняты kn + 1 голубем, по крайней мере один ящик занят k + 1 голубем.
• Проблемы четырех дней рождения используются, чтобы проанализировать случайную модель Oracle. Первая проблема используется, чтобы проанализировать атаку прообраза, вторая проблема - чтобы проанализировать атаку второго прообраза, а третья и четвертая проблемы нацелены на атаку коллизии.
• Код обнаружения модификации (MDC) - дайджест сообщения, который может доказать целостность сообщения: что сообщение не было изменено. Чтобы доказать целостность сообщения и установить подлинность происхождения данных, мы должны заменить код обнаружения модификации (MDC) на код установления подлинности сообщения (MAC). Различие между MDC и MAC в том, что MAC включает в себя безопасность передачи между передатчиком и приемником.
• Национальный Институт Стандартов и Технологии США (NIST) выработал стандарт (FIPS 198) для вложенного MAC, который часто называется кодом аутентификации сообщения, основанным на хэшировании - HMAC (хэшированный MAC ). NIST также определил другой стандарт (FIPS 113), названный CMAC, или CBCMAC.

1.6. Набор для практики

Обзорные вопросы

1. Покажите различия между целостностью сообщения и установлением подлинности сообщения
2. Определите первый критерий для криптографической хэш-функции.
3. Определите второй критерий для криптографической хэш-функции.
4. Определите третий критерий для криптографической хэш-функции.
5. Определите случайную модель Oracle и дайте описание ее приложений при анализе атак хэш-функций.
6. Установите принцип голубиных ящиков и описать его приложение при анализе хэш-функций.
7. Определите проблемы четырех дней рождения, рассмотренные в этой лекции.
8. Испробуйте каждый метод дня рождения с одной проблемой из атак хэш-функции.
9. Покажите различия между MDC и MAC.
10. Покажите различия между HMAC и CMAC.

Упражнения

1. В случайной модели Oracle: почему Oracle должен делать запись дайджеста, созданного для сообщения, и присваивать тот же самый дайджест одинаковым сообщениям?
2. Объяснить, почему секретный/открытый ключи не могут использоваться в создании MAC.
3. Игнорируя месяц рождения, сколько попыток в среднем необходимо, чтобы найти человека с такой же датой рождения, как ваша? Примите, что все месяцы имеют 30 дней.
4. Игнорируя месяц рождения, сколько попыток в среднем необходимо, чтобы найти двух человек с одинаковой датой рождения? Примите, что все месяцы имеют 30 дней.
5. Сколько попыток в среднем необходимо, чтобы найти человека того же возраста, что и вы, учитывая группу людей, рожденных после 1950?
6. Сколько попыток в среднем необходимо, чтобы найти двух человек одного и того же возраста, если мы ищем людей, рожденных после 1950?
7. Ответьте на следующие вопросы о семье из шести человек. Предположим, что их дни рождения:
   • однородно распределены в течение дней недели,
   • в течение дней месяца, в течение каждого месяца года,
   • в течение 365 дней года.

   Предположим также, что год состоит точно из 365 дней и каждый месяц - точно из 30 дней.

   • Какова вероятность, что два из членов семьи имеют один и тот же день рождения?

     Какова вероятность, что ни один из них не имеет совпадающего дня рождения?
   • Какова вероятность, что двое из членов семьи рождены в одном и том же месяце? вероятность того, что ни один из них не был рожден в одном и том же месяце?
   • Какова вероятность, что кто-то из членов семейства рожден в первый день одного из месяцев?
   • Какова вероятность, что у трех из членов семейства дни рождения приходятся на один и тот же день недели?
8. Какова вероятность совпадения дней рождения в двух классах, одного с k студентами и другого с l студентами?
9. В классе из 100 студентов какова вероятность, что два или больше студента имеют паспорта с одними и теми же последними четырьмя цифрами?
10. Есть 100 студентов в группе, и профессор разбивает ( A, B, C, D, E ) по результатам теста. Покажите, что по крайней мере одна группа будет содержать не менее 20 студентов.
11. Требует ли принцип голубиных ящиков случайного распределения голубей по ящикам?
12. Предположим, что Ева решила найти прообраз по алгоритму 1.1. Какое число раз в среднем Ева должна повторить алгоритм?
13. Предположим, что Ева решила найти коллизию по Алгоритму 1.3. Какое число раз, в среднем, Ева должна повторить алгоритм?
14. Предположим, что мы имеем очень простой дайджест сообщения. Наш дайджест сообщения (нереальный) - только одно число между 0 и 25. Дайджест первоначально установлен на 0. Криптографическая хэш-функция складывает текущее значение дайджеста со значением текущего символа (между 0 и 25). Сложение проводится по модулю 26. Идея показана на рис. 1.14. Каково значение дайджеста, если сообщение - "HELLO"? Почему этот дайджест небезопасен?
    

    
    Рис. 1.14.
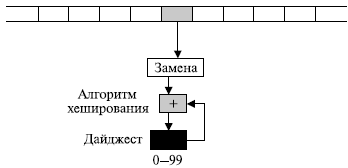
15. Попробуем увеличить сложность предыдущего упражнения. Возьмем значение текущего символа, заменим его другим числом и затем сложим с предыдущим значением из дайджеста по модулю 100. Дайджест первоначально устанавливается на 0. рис. 1.1 показывает идею. Каково значение дайджеста для сообщения " HELLO "? Почему этот дайджест - не безопасный?
    

    
    Рис. 1.15.
16. Используя модульную арифметику, найдите дайджест сообщения. рис. 1.16 иллюстрирует процедуру, которая содержит следующие шаги:
    

    
    Рис. 1.16.
    • Пусть длина дайджеста сообщения равна n битам.
    • Выберите в качестве модуля простое n - битовое число p.
    • Представьте сообщение как двоичное число и дополните сообщение с нулями (0), чтобы оно было кратно m битам.
    • Разбейте дополненное сообщение на N блоков, каждый по m бит. Обозначим каждый i -тый блок X_i.
    • Выберите начальный дайджест N битов, H₀.
    • Повторите N раз следующие действия:

      Hi  = (Hi-1 + Xi)2 mod p
    • Дайджест будет равен H_N.

    Какое значение будет иметь дайджест, если сообщение - " HELLO "? Почему этот дайджест не безопасен?
17. Ниже описывается хэш-функция, называемая модульной арифметикой безопасного хэширования (Modular Arithmetic Secure Hash -- MACH). Напишите алгоритм для вычисления дайджеста заданного сообщения. Найдите дайджест собственного сообщения.
    • Пусть длина дайджеста сообщения равна N бит.
    • Выберите два простых числа, p и q. Вычислите M = pq.
    • Представьте сообщение как двоичное число и дополните сообщение нулями, так чтобы сделать его число битов кратным N/2. N выбран как число, кратное 16, меньшее, чем число битов в M.
    • Разделите дополненное сообщение на m блоков, каждый по N/2 битов. Обозначим каждый блок X_i.
    • Прибавьте длину сообщения по модулю N/2 как двоичное число к сообщению. Это создаст сообщение длиной m+1 блоков по N/2 битов.
    • Расширьте сообщение, чтобы получить m + 1 блок, каждый по N битов, как показано ниже.

      Разделите блоки X₁ до X_m на группы по 4 бита. Вставьте 1111 перед каждой группой.

      Разделите блок X_m+1 на группы по 4 бита. Вставьте 1010 перед каждой группой.

      Назовем расширенные блоки Y₁, Y₂..., Y_m+1.
    • Выберите начальный дайджест N битов, H₀.
    • Выберите константу K из N битов.
    • Повторите m+1 раз следующие действия ( T_i и G_i - промежуточные значения). Символ || обозначает конкатенацию.

      Ti  = ((Hi+1, + Yi,) || K)257 mod M.    
      Gi = Hi mod 2N 
      Hi = Hi+1 +Gi;
    • Дайджест равен H_m+1 .
18. Напишите алгоритм в псевдокоде для решения первой проблемы дня рождения (в общей форме).
19. Напишите алгоритм в псевдокоде для решения второй проблемы дня рождения (в общей форме).
20. Напишите алгоритм в псевдокоде для решения третьей проблемы дня рождения (в общей форме).
21. Напишите алгоритм в псевдокоде для решения четвертой проблемы дня рождения (в общей форме).
22. Напишите алгоритм в псевдокоде для HMAC.
23. Напишите алгоритм в псевдокоде для CMAC.