|
Прошел экстерном экзамен по курсу перепордготовки "Информационная безопасность". Хочу получить диплом, но не вижу где оплатить? Ну и соответственно , как с получением бумажного документа? |
Целостность сообщения и установление подлинности сообщения
1.2. Случайная модель Oracle
Случайная модель Oracle была предложена в 1993 г. Белларом (Bellare) и Роджеем (Rogaway). Это идеальная математическая модель для хэш-функции. Функция, которая основана на этой модели, обладает следующими свойствами.
- Когда поступает новое сообщение любой длины, Oracle порождает и вырабатывает на выходе дайджест-сообщения фиксированной длины, которые состоят из случайных строк нулей и единиц. Это oracle-запись сообщения и дайджест-сообщения.
- Когда передается сообщение, для которого существует дайджест, oracle просто вставляет дайджест в запись.
- Дайджест для нового сообщения должен быть выбран независимо от всех предыдущих дайджестов. Это подразумевает, что модель Oracle не может использовать формулу или алгоритм для вычисления дайджеста.
Пример 1.3
Возьмем модель Oracle с таблицей и правильной монетой. Таблица имеет два столбца. Левый столбец - сообщения, дайджесты которых были выработаны. Второй столбец перечисляет дайджесты, созданные для этих сообщений. Примем, что дайджест - всегда 16 битов независимо от размера сообщения. табл. 1.1 показывает пример такой таблицы, в которой сообщение и дайджест сообщения приведены в шестнадцатеричном исчислении. Модель Oracle уже создала три дайджеста.
| Сообщение | Дайджест сообщения |
|---|---|
| 4523AB1352CDEF45126 | 13AB |
| 723BAE38F2AB3457AC | 02CA |
| AB45CD1048765412AAAB6662BE | A38B |
Теперь предположим, что возникают два события:
- а. Поступает сообщение AB1234CDS765BDAD для вычисления дайджеста. Oracle проверяет свою таблицу. Этого сообщения нет в таблице, так что сотрудник, использующий Oracle, подбрасывает в воздух свою монету 16 раз. Предположим, что результат - ООРОООРРОРООРРРО, в котором буква О представляет " Орел ", буква Р представляет " Решка ". Oracle интерпретирует О как 1 бит и Р как бит 0 и выдает 1101 1100101 10001 в двоичном коде либо DCB1 в шестнадцатеричном, как дайджест сообщения для этого сообщения, и складывает сообщение и дайджест в таблице (табл. 1.2).
- б. Сообщение 4523AB 1352CDEF45126 дается для вычисления дайджеста. Oracle проверяет свою таблицу и находит, что есть дайджест для этого сообщения в таблице (первая строка). Oracle просто выдает соответствующий дайджест ( 13AB ).
Пример 1.4
Oracle в Примере 1.3. не может использовать формулу или алгоритм, чтобы создать дайджест для сообщения.
Например, вообразим, что Oracle использует формулу h (M) = М mod n. Теперь предположим, что Oracle уже выдал h (М1) и h (М2). Если новое сообщение представлено как М3 = M1 + М2 , Oracle не должен вычислить h (М3). Новый дайджест - только [h (M1) + h (M2)] mod n, поскольку:
(M3) = (M1 + M2) mod n = M1 mod n + M2 mod n = [h(M1) + h(M2)] mod n
Это нарушает третье требование: каждый дайджест должен быть выбран беспорядочно на основе сообщения, данного Oracle.
Принцип голубиных ящиков
Первое понятие, с которым мы должны быть знакомы для того, чтобы понять анализ случайной Модели Oracle, - принцип голубиных ящиков: если n ящиков заняты n + 1 голубями, то по крайней мере один ящик занят двумя голубями. Обобщенная версия принципа голубиных ящиков: если ящиков n заняты kn +1 голубями, то по крайней мере один ящик занят k + 1 голубем.
Поскольку основная идея хэширования диктует, что дайджест должен быть короче, чем сообщение, согласно принципу голубиных ящиков могут быть конфликты. Другими словами, есть некоторые дайджесты, которые соответствуют больше чем одному сообщению; отношения между возможными сообщениями и возможными дайджестами - "много к одному".
Пример 1.5
Предположим, что сообщения в хэш-функции длиной 6 битов, дайджесты только длиной 4 бита. Тогда возможное число дайджестов (ящики) - от 24 = 16 и возможное число сообщений (голуби) - 26 = 64. Это означает n = 16 и kn + 1 = 64, так что k больше, чем 3. Это говорит о том, что по крайней мере один дайджест соответствует четырем ( k + 1 ) сообщениям.
Проблемы дня рождения
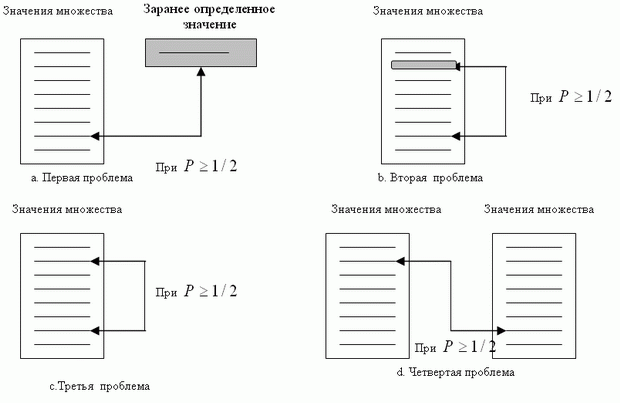
Второе понятие, которое мы должны знать перед анализом случайной модели Oracle, известно как проблема дня рождения. Обычно в курсах теории вероятностей сталкиваются с четырьмя различными проблемами дня рождения, и третья из них иногда называется парадокс дня рождения. рис. 1.7 иллюстрирует смысл каждой проблемы.
Описание проблем
Ниже приводятся проблемы дня рождения, выраженные в терминах, которые могут быть применены к хэш-функциям безопасности.
-
Проблема 1. Каково минимальное число k студентов в классной комнате, такое, что с некоторой вероятностью по крайней мере один студент имеет заранее заданный день рождения? Эта проблема может быть обобщена следующим образом. Мы имеем однородно распределенную случайную переменную с N возможными значениями (между 0 и N - 1 ). Каково минимальное число экземпляров, таких, что с некоторой вероятностью по крайней мере один экземпляр равен заранее заданному значению?
-
Проблема 2. Каково минимальное число k студентов в классной комнате, такое, что с некоторой вероятностью по крайней мере один студент имеет тот же самый день рождения, как и студент, выбранный профессором? Эта проблема может быть обобщена следующим образом. Мы имеем однородно распределенную случайную переменную с N возможными значениями (между 0 и N - 1 ) Какое минимальное число экземпляров, k, таких, что с некоторой вероятностью по крайней мере один экземпляр является равным выбранному?
-
Проблема 3. Каково минимальное число k студентов в классной комнате, такое, что с заданной вероятностью по крайней мере два студента имеют тот же самый день рождения? Эта проблема может быть обобщена следующим образом. Мы имеем однородно распределенную случайную переменную с N возможными значениями (между 0 и N - 1 ). Каково минимальное число экземпляров k, таких, что с некоторой вероятностью по крайней мере два экземпляра равны?
-
Проблема 4. Мы имеем два класса, каждый с k студентами. Каково минимальное значение A, такое, чтобы по крайней мере один студент из первой классной комнаты с некоторой вероятностью имел тот же самый день рождения, что и студент из второй классной комнаты? Эта проблема может быть обобщена следующим образом. Мы имеем однородно распределенную случайную переменную N со значениями (между 0 и N - 1 ). Мы генерируем два множества случайных значений, каждое величиной k. Каково минимальное число k, такое, что с некоторой вероятностью по крайней мере один экземпляр первого множества равен одному образцу во втором множестве?
Результаты решений
Для заинтересованных читателей решения этих проблем даются в "E. Проблемы дня рождения" . Результаты приведены в табл. 1.3.
| Проблема | Вероятность | Общее значение для k | Значение k при P = 1/2 | Число студентов ( N=365 ) |
|---|---|---|---|---|
| 1 | P =l - e-k/N | k = ln[1/(1-P) xN | k = 0,69 x N | 253 |
| 2 | P =l - e-(k-1)N | k = ln[1/(1-P) xN + 1 | k = 0,69 x N | 254 |
| 3 | P= 1 - ek(k-1)/2N | k = {2 ln [1/1-P]}1/2 xN1/2 | k= 1,18 xN1/2 | 23 |
| 4 | P =1- e- k^2/2N | k = {ln [1/1-P]}1/2 x N1/2 | k=0,83 x N1/2 | 16 |
Затемненное значение, 23, является решением классического парадокса дня рождения; если есть 23 студента в классной комнате, то с некоторой вероятностью (с P > 1/2 ) два студента имеют одинаковый день рождения (игнорируя год их рождения).
Сравнение проблем
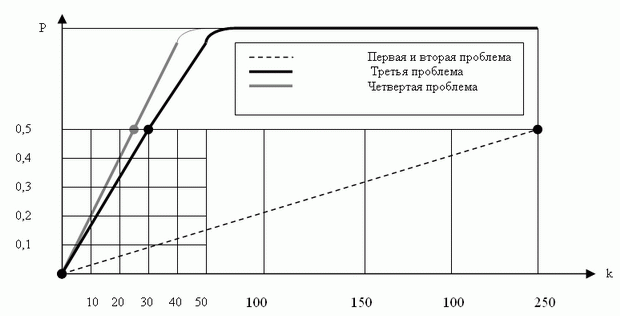
Значение k в проблемах 1 или 2 пропорционально N ; значение k в проблемах 3 или 4 является пропорциональным N1/2. Как мы увидим коротко, первые две проблемы связаны с атаками прообраза и второго прообраза; третья и четвертая проблемы связаны с атакой коллизии. Сравнение показывает, что намного более трудно начать атаку прообраза или атаку второго прообраза, чем атаку коллизии. рис. 1.8 дает граф P при различных k. Для первой и второй проблем показан один граф (значения вероятностей - очень близки). Графы для второй и третьей проблем отличаются сильнее.