|
Прошел экстерном экзамен по курсу перепордготовки "Информационная безопасность". Хочу получить диплом, но не вижу где оплатить? Ну и соответственно , как с получением бумажного документа? |
Целостность сообщения и установление подлинности сообщения
Атаки случайной модели Oracle
Чтобы лучше понимать характер хэш-функций и важность случайной модели Oracle, рассмотрим, как Ева может атаковать хэш-функцию, созданную Oracle. Предположим, что хэш-функция создает дайджесты n битов. Тогда дайджест можно представить как случайную переменную, однородно распределенную между 0 и N - 1, в которой N = 2n.Другими словами, есть возможные 2n значений для дайджеста; каждый раз Oracle случайно выбирает одно из этих значений для сообщения. Обратите внимание: это не означает, что выбор является исчерпывающим. Некоторые значения могут никогда не выбираться, но некоторые могут быть выбраны несколько раз. Мы принимаем, что алгоритм хэш-функции общедоступен и Ева знает размер дайджеста n.
Атака прообраза
Ева перехватила дайджест D = h (M) ; она хочет найти любое сообщение М', такое, что D = h (М'). Ева может создать список k сообщений и выполнить алгоритм 1.1.
Алгоритм может найти сообщение, для которого D является дайджестом, или может потерпеть неудачу. Какова вероятность успеха этого алгоритма? Очевидно, это зависит от размера списка, k, выбранного Евой. Чтобы найти вероятность, мы используем первую проблему дня рождения. Дайджест, созданный в соответствии с программой, определяет результаты случайной переменной. Вероятность успеха - P == 1 - e-k/N.
Алгоритм 1.1 Атака на прообраз
Preimage_Attack (D)
{
for (i =1 to k)
{
создать (M[i])
T <- h(M [i ]) // T - временный дайджест
if (T = D) return M[i]
}
return failure
{Какой должен быть размер k, если Ева должна достигнуть успеха по крайней мере в 50 процентах случаев? Мы показали это значение в табл. 1.3. Для первой проблемы дня рождения: 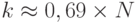 , или
, или 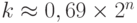 . Другими словами, чтобы Ева добилась своего более чем в 50 процентах случаев, она должна создать список дайджеста, который пропорционален 2n.
. Другими словами, чтобы Ева добилась своего более чем в 50 процентах случаев, она должна создать список дайджеста, который пропорционален 2n.
Пример 1.6
Криптографическая хэш-функция использует дайджест 64 бита. Сколько дайджестов Ева должна создать, чтобы найти первоначальное сообщение с вероятностью большей, чем 0,5?
Решение
Число дайджестов, которые будут созданы, - 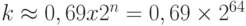 . Это большое значение. Даже если Ева сможет генерировать 230 (почти один миллиард) сообщений в секунду, требуется 0,69 x 234 секунды или больше чем 500 лет. Это означает, что дайджест сообщения размером 64 бита является безопасным относительно атаки прообраза, но, как мы увидим далее, он не защищен от атаки коллизии.
. Это большое значение. Даже если Ева сможет генерировать 230 (почти один миллиард) сообщений в секунду, требуется 0,69 x 234 секунды или больше чем 500 лет. Это означает, что дайджест сообщения размером 64 бита является безопасным относительно атаки прообраза, но, как мы увидим далее, он не защищен от атаки коллизии.
Атака второго прообраза
Ева перехватила дайджест D = h (M) и соответствующее сообщение М.; она хочет найти другое сообщение M', такое, чтобы h(M') = D. Ева может создать список из k - 1 сообщения и выполнить Алгоритм 1.2.
Алгоритм 1.2. Атака второго прообраза
Second_Preimage_Attack (D, M)
{
for (i = 1 to k - 1)
{
создать (M[i]
T <- h (M[i])
If (T = D) return M[i] // T - временный дайджест
}
return failure
}Алгоритм может найти второе сообщение, для которого D является также дайджестом, или может потерпеть неудачу. Какова вероятность успеха этого алгоритма? Очевидно, это зависит от размера списка, k, выбранного Евой. Чтобы найти вероятность положительного исхода алгоритма, мы используем вторую проблему дня рождения. Дайджест, созданный в соответствии с программой, определяет выходное значение случайной переменной. Вероятность успеха - P = 1 -e1-(k-1)/N. Какой должен быть размер k, если Ева хочет достичь успеха по крайней мере в 50 процентах случаев? Мы уже указали это значение в табл. 1.3 для второй проблемы дня рождения: 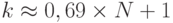 или
или 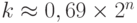 . Другими словами, чтобы Ева добилась своего более чем в 50 процентах случаев, она должна создать список дайджеста, который пропорционален 2n.
. Другими словами, чтобы Ева добилась своего более чем в 50 процентах случаев, она должна создать список дайджеста, который пропорционален 2n.
Атака коллизии
Ева должна найти два сообщения, М. и М.', такие, что h (M) = h (М.'). Она может создать список сообщений и выполнить алгоритм 1.3.
Алгоритм 1.3. Атака коллизии
Collision_Attack
{
for (i = 1 to k)
{
создать (M[i])
D[i] <- h (M[i]) // D[i] - список создаваемых дайджестов
for (j = 1 to i - 1)
{
if (D[i] = D[j] return (M[i] и M[j] )
}
}
return failure
}Алгоритм может найти два сообщения с одним и тем же дайджестом. Какова вероятность успеха этого алгоритма? Очевидно, это зависит от размера списка, k, выбранного Евой. Чтобы найти вероятность этого события, мы используем третью проблему дня рождения. Дайджест, созданный в соответствии с программой, определяет выходное значение случайной переменной. Вероятность успеха - P = 1 - e1-(k-1)/2N. Какой должен быть размер k, если Ева хочет достичь успеха по крайней мере в 50 процентах случаев? Мы уже указали это значение в табл. 1.3 для третьей проблемы дня рождения: 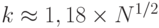 , или
, или 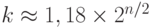 . Другими словами, чтобы Ева добилась своего более чем в 50 процентах случаев, она должна создать список дайджеста, который пропорционален 2n/2.
. Другими словами, чтобы Ева добилась своего более чем в 50 процентах случаев, она должна создать список дайджеста, который пропорционален 2n/2.
Пример 1.7
Криптографическая хэш-функция использует дайджест 64 бита. Сколько дайджестов Ева должна создать, чтобы найти два сообщения с тем же самым дайджестом с вероятностью больше чем 0,5?
Решение
Число дайджестов, которые будут созданы, 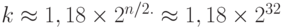 . Если Ева может проверить 220 (почти один миллион) сообщений в секунду, потребуется 1,18 x 212 секунд, или меньше чем два часа. Это означает, что дайджест сообщения размера 64 бита небезопасен относительно атаки коллизии.
. Если Ева может проверить 220 (почти один миллион) сообщений в секунду, потребуется 1,18 x 212 секунд, или меньше чем два часа. Это означает, что дайджест сообщения размера 64 бита небезопасен относительно атаки коллизии.
Дополнительная атака коллизии
Предыдущая атака коллизии не может быть полезна для Евы - ей приходится создать два сообщения, одно реальное и одно фиктивное, которые имеют одно и то же значение хэш-функции. Каждое сообщение должно быть значащим. Предыдущий алгоритм не обеспечивает устойчивость коллизии, решение состоит в том, чтобы создать два значащих сообщения, но добавить избыточность к сообщению или модифицировать сообщение, чтобы изменить содержание слова, или прибавлять некоторые избыточные слова, и так далее, в сообщение, не изменяя значение его хэша. Например, множество сообщений может быть создано из первого сообщения - добавлением пробелов или изменением слова, когда некоторые слова дополняются окончаниями.
Второе сообщение может также создать множество сообщений. Если обозначить первоначальное сообщение М, а фиктивное сообщение - М', Ева создает k различных вариантов М (M1, M2 ,... , Mk) и k различных вариантов М' (M'1, M'2 ,... , M'k). Затем Ева использует алгоритм 1.4 для того, чтобы начать атаку.
Алгоритм 1.4. Дополнительная атака коллизии
Alternate_Collision _Attack (M[k], M'[k])
{
for (i = 1 to k)
{
D[i] <- h ([M[i])
D'[i] <- h [M'[i])
if (D[i] = D'[j] return (M[i], M'[j])
}
return failure
]Какова вероятность успеха этого алгоритма? Очевидно, это зависит размера списка k, выбранного Евой. Чтобы найти вероятность, мы используем четвертую проблему дня рождения. Два списка дайджеста, созданные в соответствии с программой, определяют два выходных значения случайной Вероятность успеха равна 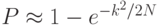 . Какой должен быть размер k, если Ева хочет достичь успеха по крайней мере в 50 процентах случаев? Мы уже указали это значение в таблице для четвертой проблемы дня рождения:
. Какой должен быть размер k, если Ева хочет достичь успеха по крайней мере в 50 процентах случаев? Мы уже указали это значение в таблице для четвертой проблемы дня рождения: 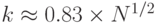 или
или 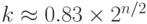 .
Другими словами, чтобы Ева добилась своего более чем в 50 процентах случаев, она должна создать список дайджеста, который пропорционален 2n/2.
.
Другими словами, чтобы Ева добилась своего более чем в 50 процентах случаев, она должна создать список дайджеста, который пропорционален 2n/2.
Итоги атак
Таблица 1.4 показывает уровень сложности для каждой атаки, если дайджест имеет длину n бит.
| Атака | Значение при P =1/2 | Порядок верхнего предела |
|---|---|---|
| Прообраз |  |
2n |
| Второй прообраз |  |
2n |
| Коллизия | 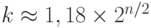 |
2n/2. |
| Дополнительная коллизия | 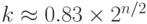 |
2n/2 |
Таблица 1.4 показывает, что порядок или сложность атаки для атаки коллизии является намного меньшим, чем для прообраза или атак второго прообраза. Если алгоритм хэша является стойким к атакам коллизии, мы можем не волноваться о безопасности атак прообраза и атак второго прообраза.
Пример 1.8
Первоначально хэш-функции с дайджестом на 64 бита, как полагали, были стойкими к атакам коллизии. Но с увеличением скорости обработки сегодня все обнаружили, что эти хэш-функции больше не безопасны. Ева нуждается только в 264/2 = 232 испытаний, чтобы начать атаку с вероятностью 1/2 или больше. Предположим, что она может выполнить 220 (один миллион) испытаний в секунду. Она может провести атаку за 232 / 220 = 212 секунд (почти час!).
Пример 1.9
MD5 (см. "Криптографические хэш-функции" ), который был одной из стандартных хэш-функций в течение долгого времени, создает дайджесты в 128 битов. Чтобы провести атаку коллизии, противник должен провести 264 (2128/2) испытаний алгоритма коллизии. Даже если противник может выполнить 230 (больше чем один миллиард) испытаний в секунду, требуется 234 секунды (больше чем 500 лет), чтобы провести атаку. Этот тип атаки базируется на случайной модели Oracle. Было доказано, что MD5 может быть атакован за менее чем 264 испытаний - из-за структуры алгоритма.
Пример 1.10
SHA-1 (см. "Криптографические хэш-функции" ), стандартная хэш-функция, разработанная NIST, создает дайджесты в 160 битов. Чтобы провести атаку коллизии, противник должен исполнить 2160/2 = 280 испытания в алгоритме коллизии. Даже если противник может выполнить 230 (больше чем один миллиард) испытаний в секунду, требуется 250 секунд (больше чем десять тысяч лет), чтобы начать атаку. Однако исследователи обнаружили некоторые особенности функции, которые позволяют провести атаку на эту хэш-функцию за меньшее время, чем вычисленное выше.
Пример 1.11
Новая хэш-функция, которая, вероятно, станет NIST-стандартом, - SHA-512 (см. "Криптографические хэш-функции" ) имеет дайджест на 512 битов. Эта функция явно стойкая к атакам коллизии, основанным на случайной модели Oracle. Требуется от 2512/2 до 2256 испытаний, чтобы найти коллизию с вероятностью 1/2.
Атаки структуры
Все обсуждения, связанные с атаками хэш-функций, базировались на идеальной криптографической хэш-функции, которая похожа на Oracle. Хотя этот тип анализа обеспечивает систематическую оценку алгоритмов, практически хэш-функции могут иметь некоторые внутренние структуры, которые могут сделать их намного слабее.
Невозможно найти хэш-функцию, которая создает дайджесты, чтобы она делала их полностью случайными. Противник может иметь другие инструментальные средства для того, чтобы атаковать хэш-функцию. Одно из этих инструментальных средств, например, атака сведения к середине, которая обсуждалась в предыдущем курсе для двукратного DES. Мы увидим в следующих лекциях, что некоторые хэш-алгоритмы поддаются этому типу атаки. Эти типы хэш-функции далеки от идеальной модели, и нужно их избегать.
