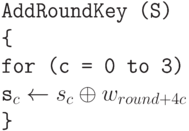|
Прошел экстерном экзамен по курсу перепордготовки "Информационная безопасность". Хочу получить диплом, но не вижу где оплатить? Ну и соответственно , как с получением бумажного документа? |
Преобразования
Смешивание
Подстановка, которая делается преобразованием SubByte, изменяет значение байта, основанное только на первоначальном значении и входе в таблице; процесс не включает соседние байты. Мы можем сказать, что SubByte — внутрибайтовое преобразование. Перестановка, которая делается ShiftRows-преобразованием, обменивает местами байты, не переставляя биты в байтах. Мы можем сказать, что ShiftRows — преобразование обмена байтами. Теперь нам нужно внутрибайтовое преобразование, изменяющее биты в байте и основанное на битах в соседних байтах. Мы должны смешать байты, чтобы обеспечить рассеивание на разрядном уровне.
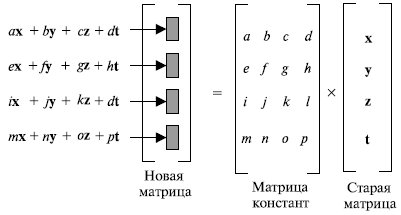
Преобразование смешивания изменяет содержание каждого байта, преобразовывая четыре байта одновременно и объединяя их, чтобы получить четыре новых байта. Чтобы гарантировать, что каждый новый байт будет отличаться от другого (даже если все четыре байта те же самые), процесс сначала умножает каждый байт на различный набор констант и затем смешивает их. Смешивание может быть обеспечено матричным умножением. Как мы обсуждали в лекциях 2-3, когда мы умножаем квадратную матрицу на матрицу-столбец, результат — новая матрица-столбец. После того как матрица умножена на значения строки в матрице констант, каждый элемент в новой матрице зависит от всех четырех элементов старой матрицы. Рисунок 9.11 иллюстрирует эту идею.
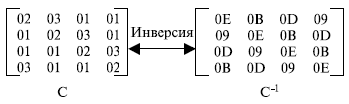
AES определяет преобразование, называемое MixColumns. Для применения такого преобразования вводится также обратное преобразование, называемое InvMixColumns. Рисунок 9.12 показывает матрицу констант, используемую для этих преобразований. Эти две матрицы инверсны друг другу, когда элементы интерпретируются как слова из 8-ми битов (или полиномы) с коэффициентами в GF (28). Доказательство мы оставляем как упражнение.
MixColumns
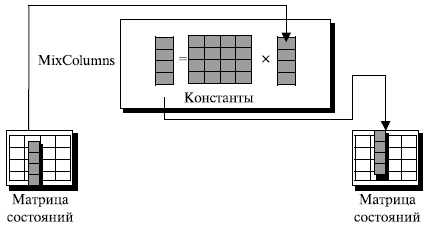
Преобразование MixColumns работает на уровне столбца; оно преобразовывает каждый столбец матрицы состояний в новый столбец. Это преобразование — фактически матричное умножение столбца матрицы состояний и квадратной матрицы констант. Байты в столбце матрицы состояний и в матрице констант интерпретируются как слова по 8 битов (или полиномы) с коэффициентами в GF (2). Умножение байтов выполняется в GF(28) по модулю (10001101) или (x8 + x4 +, x3 + x + 1). Сложение — это применение операции ИСКЛЮЧАЮЩЕЕ ИЛИ (XOR) к словам по 8 бит. Рисунок 9.13 показывает преобразование MixColumns.
InvMixColumns
Преобразование InvMixColumns похоже на MixColumns-преобразование. Если две матрицы констант инверсны друг другу, то легко доказать, что эти два преобразования также инверсны друг другу.
Алгоритм
Алгоритм 9.3. — программа для преобразования MixColumns.
9.3. Программа на псевдокоде для преобразования MixColumns
Алгоритмы MixColumns и InvMixColumns включают умножение и сложение в поле GF(28). Как мы видели влекциях 5-6, есть простой и эффективный алгоритм для умножения и сложения в этом поле. Однако чтобы показать характер алгоритма (преобразование одного столбца одновременно), мы используем процедуру, называемую mixcolumn. Она может быть вызвана алгоритмом четыре раза. Процедура mixcolumn просто умножает строки матрицы констант на столбец в матрицы состояний. В вышеупомянутом алгоритме оператор (•), используемый в процедуре mixcolumn, — умножение в поле GF(28). Оно может быть заменено простой процедурой, как это уже рассматривалось в лекциях 5-6. Программу для InvMixColumns оставляем как упражнение.
Пример 9.5
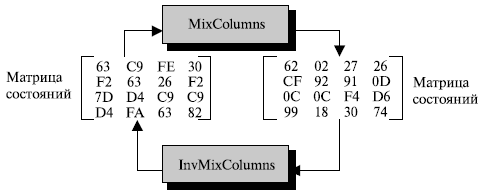
Рисунок 9.14 показывает, как матрица состояний преобразуется, используя преобразование MixColumns. Рисунок также показывает, что преобразование InvMixColumns создает первоначальный текст.
Обратите внимание, что байты, которые равны между собой в старой матрице состояний, больше не равны в новой матрице состояний. Например, два байта F2 во второй строке изменены на CF и 0D.
Добавление ключей
Вероятно, самое важное преобразование — это преобразование, которое включает ключ шифра, Все предыдущие преобразования используют известные алгоритмы, которые являются обратимыми. Если не добавлять ключевой шифр в каждом раунде, противник очень просто найдет исходный текст по данному ему зашифрованному тексту. В этом случае хранитель тайны Алисы и Боба — один единственный ключ шифра.
AES использует процесс, названный ключевым расширением (мы его обсудим позже), который из ключа шифра создает Nr+1 ключей раунда. Каждые ключи раунда — 128-битовой длины и обрабатываются они как четыре слова по 32 бита. Для добавления ключа к матрице состояний каждое слово рассматривается как матрица-столбец.
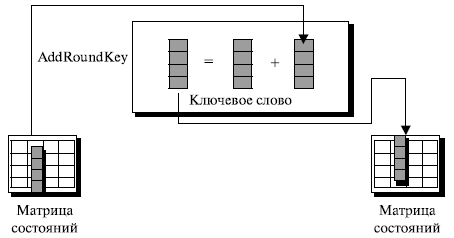
AddRoundKey
AddRoundKey обрабатывает в один момент времени один столбец. Он подобен MixColumns. MixColumns умножает квадратную матрицу констант на каждый столбец матрицы состояний. AddRoundKey складывает ключевое слово раунда с каждым столбцом матрицы состояний. В MixColumns применяется матричное умножение; в AddRoundKey — операции сложения и вычитания. Так как сложение и вычитание в этом поле одни и те же, AddRoundKey инверсен сам себе. Рисунок 9.15 показывает преобразование AddRoundKey.
Алгоритм
Преобразование AddRoundKey может быть представлено как операция ИСКЛЮЧАЮЩЕЕ ИЛИ (XOR) каждой колонки матрицы состояний с соответствующим ключевым словом. Мы еще будем обсуждать, как расширяется ключ шифрования во множестве ключевых слов, но в данном случае мы определим преобразование, как это показано в алгоритме 9.4. Заметим, что sc и wround +4c матрицы — колонки  .
.
9.4. Преобразование AddRoundKey
Напомним, что оператор  здесь означает операцию ИСКЛЮЧАЮЩЕЕ ИЛИ (XOR) для двух колонок матрицы, каждая из 4-х байт. Описание этой простой процедуры оставим для упражнений.
здесь означает операцию ИСКЛЮЧАЮЩЕЕ ИЛИ (XOR) для двух колонок матрицы, каждая из 4-х байт. Описание этой простой процедуры оставим для упражнений.