|
Прошел экстерном экзамен по курсу перепордготовки "Информационная безопасность". Хочу получить диплом, но не вижу где оплатить? Ну и соответственно , как с получением бумажного документа? |
Поля
Сложение
Теперь определим операцию сложения для полиномов с коэффициентом в GF(2). Операция сложения очень простая: мы складываем коэффициенты соответствующих элементов полинома в поле GF(2). Обратите внимание, что сложение двух полиномов степени n – 1 всегда дает полином со степенью n – 1 — это означает, что мы не должны использовать вычитание из модуля их результата.
Пример 6.4
Произведем сложение  в GF(28). Мы используем символ
в GF(28). Мы используем символ  для обозначения полиномиального сложения. Ниже показана процедура
для обозначения полиномиального сложения. Ниже показана процедура

В упрощенном полиноме (показан справа) сохранены элементы с коэффициентом 1 и удалены элементы с коэффициентом 0. Кроме того, удалены совпадающие элементы обоих полиномов, а несовпадающие сохраняются. Другими словами, x5, x3, и x1 сохраняются, а x2, который является совпадающим в этих двух полиномах, удален.
Пример 6.5
Поскольку сложение в GF(2) означает операцию ИСКЛЮЧАЮЩЕЕ ИЛИ (XOR), мы можем получить результат ИСКЛЮЧАЮЩЕГО ИЛИ для этих двух слов бит за битом. В предыдущем примере x5 + x2 + x есть 00100110, или полином, и x3 + x2 + 1 есть 00001101. Результат — 00101011 или, в полиномиальном обозначении, x5 + x3 + x + 1.
Аддитивный нейтральный элемент — тождество. Аддитивный нейтральный элемент полинома — нулевой полином (полином со всеми коэффициентами, равными нулю), потому что, прибавляя этот полином к самому себе, в результате получаем нулевой полином.
Аддитивная инверсия полинома с коэффициентами в GF(2) — сам полином. Это означает, что операция вычитания та же самая, что и операция сложения.
Сложение и операции вычитания на полиномах — та же самая операция.
Умножение
Умножение в полиномах — сумма умножения каждого элемента одного полинома с каждым элементом второго полинома. Однако необходимо отметить три особенности.
Первая: умножение коэффициента проводится в поле GF(2).
Вторая: умножение xi на xj дает результат xi+j.
Третья: умножение может создать элементы со степенью большей, чем n–1, и это означает, что результат должен быть уменьшен с использованием полинома-модуля.
Сначала покажем, как умножить два полинома согласно вышеупомянутому определению. Позже будет дан более эффективный алгоритм, который может использоваться компьютерной программой.
Пример 6.6
Найдите результат 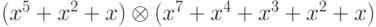 в GF(28) с неразлагаемым полиномом (x8 + x4 + x3 + x + 1). Обратите внимание, что для обозначения умножения двух полиномов используется символ
в GF(28) с неразлагаемым полиномом (x8 + x4 + x3 + x + 1). Обратите внимание, что для обозначения умножения двух полиномов используется символ  .
.
Решение
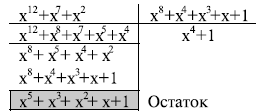
Сначала умножаем эти два полинома так, как мы это делали в обычной алгебре. Обратите внимание, что в этом процессе пара элементов с равной степенью удаляется. Например, результат x9 + x9 полностью удален, потому что он нулевой полином, по причине, которую мы обсуждали раньше при рассмотрении операции сложения.
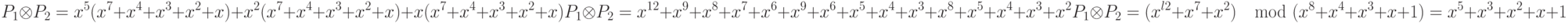
Чтобы найти конечный результат, разделим полином степени 12 на полином степени 8 (модуль) и сохраним только остаток. Процесс деления тот же самый, что и в обычной алгебре, но мы должны помнить, что здесь вычитание то же самое, что и сложение. Рисунок 6.3 показывает процесс деления.
Мультипликативное тождество — всегда равно 1. Например, в GF(28) мультипликативная инверсия — в побитном изображении 00000001.
Мультипликативная инверсия. Поиск мультипликативной инверсии требует привлечения расширенного алгоритма Евклида. Алгоритм Евклида должен быть применен к модулю и полиному, выполнение алгоритма является таким же, как и для целых чисел.
Пример 6.7
В GF(24) найдите инверсию (x2 + 1) mod (x4 + x + 1).
Решение
Мы используем расширенный евклидов алгоритм, как это показано в таблице 6.2:
Это означает, что (x2 + 1) -1 mod (x4 + x + 1) есть (x3 + x + 1). Ответ может быть проверен просто: надо перемножить эти два полинома и найти остаток. В этом случае результат деления на модуль равен
![[(x^{2} + 1) \otimes (x^{3} + x + 1)] \mod (x^{4} + x + 1) = 1](/sites/default/files/tex_cache/58678c7b37dc0752fddb9cf1e71af5ad.png)
Пример 6.8
В GF(28) найдите инверсию (x5) mod (x8 + x4 + x3 + x + 1).
Решение
Будем использовать расширенный евклидов алгоритм, как это показано в Таблице 6.3:
| q | rj | r2 | r | tj | t2 | t |
|---|---|---|---|---|---|---|
| (x3) | (x8+x4+x3+x+1) | (x5) | (x4+x3+x2+x+1) | (0) | (1) | (x3) |
| (x+1) | (x5) | (x4+x3+x+1) | (x3+x2+1) | (1) | (x3) | (x4+x3+1) |
| (x) | (x4+x3+x+1) | (x3+x2+1) | (1) | (x3) | (x4+x3+1) | (x5+x4+x2+x) |
| (x3+x2+1) | (1) | (0) | (x4+x3+1) | (x5+x4+x2+x) | (0) | |
| (1) | (0) | (x5+x4+x2+x) | (0) |
Это означает, что (x5)-1 mod (x8 + x4 + x3 + x + 1) есть (x5 + x4 + x2 + x).
Результат может быть легко проверен умножением этих двух полиномов и определением остатка деления по модулю.
![[(x^{5}) \otimes (x^{5}+x^{4}+x^{3}+x)] \mod (x^{8}+x^{4}+x^{3}+x+1) =](/sites/default/files/tex_cache/f18e0cfa88588a5425e4318d1eb1aef2.png)
Умножение, использующее компьютер
Операция деления порождает проблему написания эффективной программы умножения двух полиномов. Лучший алгоритм для компьютерной реализации использует неоднократное умножение уменьшенного полинома на x. Например, вместо того чтобы находить результат  , программа находит результат
, программа находит результат 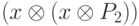 . Преимущества этой стратегии будет обсуждаться далее, но сначала рассмотрим пример, чтобы проиллюстрировать алгоритм.
. Преимущества этой стратегии будет обсуждаться далее, но сначала рассмотрим пример, чтобы проиллюстрировать алгоритм.
Пример 6.9
Найдите результат умножения P1 = (x5 + x2 + x) на P2 = (x7 + x4 + x3 + x2 + x) в поле GF(28) с неприводимым полиномом (x8 + x4 + x3 + x + 1), используя алгоритм, изложенный выше.
Решение
Процесс показан в таблице 6.4. Мы сначала находим промежуточный результат умножения x0, x1, x2, x3, x4 и x5. Заметим, что необходимы только три составляющие произведения  для m от 0 до 5, каждое вычисление зависит от предыдущего результата.
для m от 0 до 5, каждое вычисление зависит от предыдущего результата.
| Степень | Операция | Новый результат | Вычитание |
|---|---|---|---|
x0  P2 P2
|
x7+x4+x3+x2+x | НЕТ | |
x1  P2 P2
|
x  (x7+x4+x3+x2+x) (x7+x4+x3+x2+x) |
x5+x2+x+1 | ДА |
x2  P2 P2
|
x  (x5+x2+x+1) (x5+x2+x+1) |
x6+x3+x2+x | НЕТ |
x3  P2 P2
|
x  (x6+x3+x2+x) (x6+x3+x2+x) |
x7+x4+x3+x2 | НЕТ |
x4  P2 P2
|
x  (x7+x4+x3+x2) (x7+x4+x3+x2) |
x5+x+1 | ДА |
x5  P2 P2
|
x  (x5+x+1) (x5+x+1) |
x6+x2+x | НЕТ |
| P1 x P2 = (x6+x2+x)+(x6+x3+x2+x)+(x5+x2+x+1) = x5+x3+x2+x+1 | |||
Рассмотренный выше алгоритм имеет два преимущества. Первое — умножение полинома на x может быть выполнено простым сдвигом одного бита в n -битовом слове; операция может быть реализована на любом языке программирования. Второе — результат может быть использован, если максимальная степень полинома n–1. В этом случае сокращение может быть сделано просто с помощью применения операции ИСКЛЮЧАЮЩЕЕ ИЛИ с заданным модулем. В нашем примере самая высокая степень — только 8. Мы можем разработать простой алгоритм для нахождения промежуточных результатов.
- Если старший разряд предыдущего результата равен 0, тогда надо сдвинуть предыдущий результат на один бит влево.
- Если старший бит предыдущего результата равен 1: а. надо сдвинуть на один бит влево, и б. применить к нему операцию ИСКЛЮЧАЮЩЕЕ ИЛИ с модулем, исключив из этой операции старший разряд.
Повторим пример 6.9 для двоичной последовательности размером 8 бит.
Пусть P1 = 00100110, P2 = 10011110, модуль = 100011010 (девять битов). Обозначим операцию ИСКЛЮЧАЮЩЕЕ ИЛИ как  . Пример приведен в таблице 6.5.
. Пример приведен в таблице 6.5.
В этом случае для умножения этих двух полиномов нам надо только пять операций левого сдвига и четыре ИСКЛЮЧАЮЩЕЕ ИЛИ. Вообще, для умножения двух полиномов степени n-1 необходимо максимально (n–1) операций левого сдвига и 2n операций ИСКЛЮЧАЮЩЕЕ ИЛИ.
Пример 6.10
Поле GF(23) состоит из 8 элементов. Покажем умножение и сложение таблиц для этого поля, используя неприводимый полином x3+x2+1. Мы будем оперировать с трехбитовым словом и полиномом. Заметим, что имеется два полинома третьей степени (см. таблицу 6.1). Другой полином (x3 + x + 1) для умножения имеет таблицу, полностью отличающуюся от первой. Таблица 6.6 показывает сложение. Затемненные клетки (нулевые) дают обратные пары для сложения.
Таблица 6.7 показывает умножение. Затемненные клетки (единичные) дают обратные пары при умножении.