|
Не могу найти требования по оформлению выпускной контрольной работы по курсу профессиональной переподготовки "Менеджмент предприятия" |
Статистика нечисловых данных
Асимптотическое поведение решений экстремальных статистических задач. Если проанализировать приведенные выше постановки и результаты, особенно теоремы 1 и 3, то становится очевидной возможность их обобщения. Так, доказательства этих теорем практически не меняются, если считать, что функция 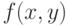 определена на декартовом произведении бикомпактных пространств
определена на декартовом произведении бикомпактных пространств  и
и  . Тогда можно считать, что элементы выборки лежат в
. Тогда можно считать, что элементы выборки лежат в  , а
, а  - пространство параметров, подлежащих оценке. Пусть, например, выборка взята из распределения с плотностью
- пространство параметров, подлежащих оценке. Пусть, например, выборка взята из распределения с плотностью 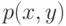 . Если положить
. Если положить  то задача нахождения эмпирического среднего переходит в задачу оценивания неизвестного параметра
то задача нахождения эмпирического среднего переходит в задачу оценивания неизвестного параметра  методом максимального правдоподобия, а законы больших чисел переходят в утверждения о состоятельности этих оценок в случае пространств
методом максимального правдоподобия, а законы больших чисел переходят в утверждения о состоятельности этих оценок в случае пространств  и
и  общего вида. В случае функции
общего вида. В случае функции 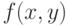 общего вида можно говорить об определении и состоятельности так называемых оценок минимального контраста. Частными случаями этих оценок являются, например, устойчивые (робастные) оценки Тьюки-Хубера (см.
"Проблемы устойчивости эконометрических процедур"
10), оценки параметров в задачах аппроксимации (параметрической регрессии) в пространствах произвольной природы.
общего вида можно говорить об определении и состоятельности так называемых оценок минимального контраста. Частными случаями этих оценок являются, например, устойчивые (робастные) оценки Тьюки-Хубера (см.
"Проблемы устойчивости эконометрических процедур"
10), оценки параметров в задачах аппроксимации (параметрической регрессии) в пространствах произвольной природы.
Можно пойти и дальше в обобщении законов больших чисел. Пусть известно, что при каждом конкретном  при безграничном росте
при безграничном росте  имеет быть сходимость по вероятности
имеет быть сходимость по вероятности 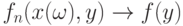 .
.
В каких случаях и в каком смысле
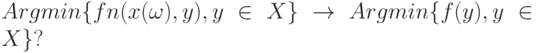
Причем здесь можно под n понимать натуральное число. А можно рассматривать "сходимость по фильтру" в смысле Картана и Бурбаки [29, с.118]. В частности, описывать ситуацию вектором, координаты которого - объемы нескольких выборок, и все они безгранично растут. В классической математической статистике такие постановки рассматривать не любят.
Поскольку, как уже отмечалось, основные задачи прикладной статистики можно представить в виде оптимизационных задач, то ответ на поставленный вопрос дает возможность единообразного подхода к изучению асимптотики решений разнообразных экстремальных статистических задач. Одна из возможных формулировок дана и обоснована выше. Другая - в работе [28]. Она основана на использовании понятий асимптотической равномерной разбиваемости и координатной асимптотической равномерной разбиваемости. С помощью указанных подходов удается стандартным образом обосновывать состоятельность оценок характеристик и параметров в основных задачах прикладной статистики. К сожалению, в рамках настоящей лекции нет возможности подробнее остановиться на проблеме оценивания.
Рассматриваемую тематику можно развивать дальше, в частности, рассматривать пространства  и
и  , не являющиеся бикомпактными, а также изучать скорость сходимости эмпирических средних к теоретическим.
, не являющиеся бикомпактными, а также изучать скорость сходимости эмпирических средних к теоретическим.
Медиана Кемени и экспертные оценки. Рассмотрим частный случай пространств нечисловой природы - пространство бинарных отношений на конечном множестве  и его подпространства. Как известно, каждое бинарное отношение
и его подпространства. Как известно, каждое бинарное отношение  можно описать матрицей
можно описать матрицей 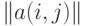 из 0 и 1, причем
из 0 и 1, причем 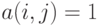 тогда и только тогда
тогда и только тогда  и
и 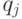 находятся в отношении
находятся в отношении  , и
, и 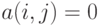 в противном случае.
в противном случае.
Определение 4. Расстоянием Кемени между бинарными отношениями  и
и 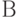 , описываемыми матрицами
, описываемыми матрицами 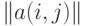 и
и 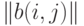 соответственно, называется
соответственно, называется
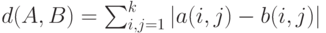
Замечание. Иногда в определение расстояния Кемени вводят множитель, зависящий от  .
.
Как уже отмечалось, указанное расстояние введено американским исследователем Дж. Кемени в 1950-х годах и получило в нашей стране известность благодаря монографии [24], в которой оно получено для упорядочений (т.е. ранжировок, в которых допускаются связи, или кластеризованных ранжировок - см. "Эконометрические методы проведения экспертных исследований и анализа оценок экспертов" ) исходя из некоторой системы аксиом. Некоторое время казалось, что аксиоматический подход избавляет от субъективизма в выборе расстояния, а потому - от субъективизма в выборе способа усреднения бинарных отношений. Монография [24] породила поток работ, в которых с помощью различных систем аксиом вводились те или иные расстояния в пространствах объектов нечисловой природы (в обзоре [23] на эту тему - 161 ссылка на соответствующие публикации). В итоге произвол в выборе метрик отодвинут на уровень произвола в выборе систем аксиом.
Определение 5. Медианой Кемени для выборки, состоящей из бинарных отношений, называется эмпирическое среднее, построенное с помощью расстояния Кемени.
Поскольку число бинарных отношений на конечном множестве конечно, то эмпирические и теоретические средние для произвольных показателей различия существуют и справедливы законы больших чисел, описанные формулами (21) и (22) выше.
Бинарные отношения, в частности, упорядочения, часто используются для описания мнений экспертов. Тогда расстояние Кемени измеряет близость мнений экспертов, а медиана Кемени позволяет находить итоговое усредненное мнение комиссии экспертов. Расчет медианы Кемени обычно включают в информационное обеспечение систем принятия решений с использованием оценок экспертов. Речь идет, например, о математическом обеспечении автоматизированного рабочего места "Математика в экспертизе" (АРМ "МАТЭК"), предназначенного, в частности, для использования при проведении экспертиз в задачах экологического страхования. Поэтому представляет большой практический интерес численное изучение свойств медианы Кемени при конечном объеме выборки. Такое изучение дополняет описанную выше асимптотическую теорию, в которой объем выборки предполагается безгранично возрастающим 
Компьютерное изучение свойств медианы Кемени при конечных объемах выборок. С помощью специально разработанной программной системы В.Н. Жихаревым был проведен ряд серий численных экспериментов по изучению свойств выборочных медиан Кемени. Представление о полученных результатах дается приводимой ниже табл.8.1, взятой из статьи [30]. В каждой серии методом статистических испытаний определенное число раз моделировался случайный и независимый выбор экспертных ранжировок, а затем находились все медианы Кемени для смоделированного набора мнений экспертов. При этом в сериях 1-5 распределение ответа эксперта предполагалось равномерным на множестве всех ранжировок, а в серии 6 это распределение являлось монотонным относительно расстояния Кемени с некоторым центром (о понятии монотонности см. выше), т.е. вероятность выбора определенной ранжировки убывала с увеличением расстояния Кемени этой ранжировки от центра. Таким образом, серии 1-5 соответствуют ситуации, когда у экспертов нет почвы для согласия, нет группировки их мнений относительно некоторого единого среднего группового мнения, в то время как в серии 6 есть единое мнение - описанный выше центр, к которому тяготеют ответы экспертов.
Результаты, приведенные в табл.8.1, можно комментировать разными способами. Неожиданным явилось большое число элементов в выборочной медиане Кемени - как среднее, так и особенно максимальное. Одновременно обращает на себя внимание убывание этих чисел при росте числа экспертов и особенно при переходе к ситуации реального существования группового мнения (серия 6). Достаточно часто один из ответов экспертов входит в медиану Кемени (т.е. пересечение множества ответов экспертов и медианы Кемени непусто), а диаметр медианы как множества в пространстве ранжировок заметно меньше диаметра множества ответов экспертов. По этим показателям - наилучшее положение в серии 6. Грубо говоря, всяческие "патологии" в поведении медианы Кемени наиболее резко проявляются в ситуации, когда ее применение не имеет содержательного обоснования, т.е. когда у экспертов нет основы для согласия, их ответы равномерно распределены на множестве ранжировок.
Увеличение числа испытаний в 10 раз при переходе от серии 1 к серии 5 не очень сильно повлияло на приведенные в таблице характеристики, поэтому представляется, что суть дела выявляется при числе испытаний (в методе Монте-Карло), равном 100 или даже 50. Увеличение числа объектов или экспертов увеличивает число элементов в рассматриваемом пространстве ранжировок, а потому уменьшается частота попадания какого-либо из мнений экспертов внутрь медианы Кемени, а также отношение диаметра медианы к диаметру множества экспертов, число элементов медианы Кемени (среднее и максимальное). Можно сказать, что увеличение числа объектов или экспертов уменьшает степень дискретности задачи, приближает ее к непрерывному случаю, а потому уменьшает выраженность различных "патологий".
Есть много интересных результатов, которые мы здесь не рассматриваем. Они связанны, в частности, со сравнением медианы Кемени с другими методами усреднения мнений экспертов, например, с нахождением итогового упорядочения по методу средних рангов, а также с использованием малых окрестностей ответов экспертов для поиска входящих в медиану ранжировок, с теоретической и численной оценкой скорости сходимости в законах больших чисел.
