Двусторонняя торговля и теорема Вильямса
Теорема Вильямса: общий случай
Итак, мы готовы сформулировать наш основной результат.
Теорема 7.3. (Вильямса) Рассмотрим проблему социального выбора с квазилинейными предпочтениями. Предположим также, что
- множества типов
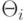 представляют собой связные открытые подмножества
представляют собой связные открытые подмножества 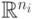 ,
, - ожидаемые (interim) внутренние ценности агентов
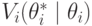
непрерывно дифференцируемы на
 в точках, в которых
в точках, в которых  .
.
Тогда механизмы VCG являются правдивыми и эффективными для этой задачи, и ожидаемые (interim) внутренние ценности агентов 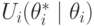 любого правдивого и эффективного механизма совпадают с ценностями одного из механизмов VCG.
любого правдивого и эффективного механизма совпадают с ценностями одного из механизмов VCG.
Как обычно, a good formula stays for ever, и формула, которая получится по дороге, будет ничуть не менее важной, чем сама теорема классификации. Давайте ее тоже сформулируем.
Теорема 7.4. (Вильямса) В условиях теоремы 7.3 функция доходности любого правдивого эффективного механизма для любой пары типов 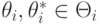 имеет вид
имеет вид
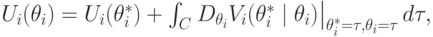
где  — гладкая кривая от
— гладкая кривая от 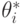 к
к 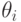 внутри
внутри 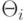 ,
, 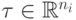 .
.
Доказательство. Обозначим через 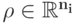 некоторый единичный вектор, через
некоторый единичный вектор, через 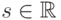 — некоторое вещественное число. Правдивость гласит, что для всех
— некоторое вещественное число. Правдивость гласит, что для всех 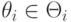
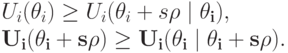
Вычтем 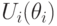 из обеих частей первого неравенства; получается:
из обеих частей первого неравенства; получается:
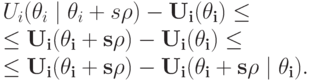
Сократим там 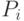 слева и справа (они не зависят от истинной ценности, а только от сообщаемой) и разделим на
слева и справа (они не зависят от истинной ценности, а только от сообщаемой) и разделим на  :
:
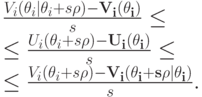
Устремим теперь 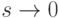 . По условию о дифференцируемости
. По условию о дифференцируемости 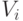 , левая часть сходится к производной функции
, левая часть сходится к производной функции 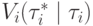 по направлению
по направлению 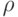 в точке
в точке 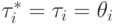 .
.
Правая часть раскладывается на
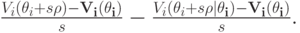
Первое слагаемое по тем же причинам сходится к производной  по
по 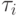 по направлению
по направлению 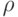 в
в  , а второе слагаемое — к производной
, а второе слагаемое — к производной 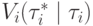 по
по 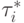 по направлению
по направлению 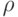 в
в 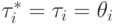 .
.
Таким образом, вся правая часть сходится к производной функции 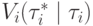 по
по 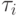 по направлению
по направлению 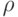 в точке
в точке 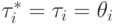 . Значит,
. Значит,
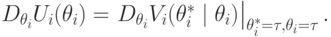
Отсюда следует утверждение теоремы, потому что производная по предположению непрерывна.
Это весьма показательный метод доказательства. По сути это развитие исходной идеи Майерсона в максимальной (или близкой к тому) общности. Видно, что откуда берется во всех таких теоремах: нужно взять изменение (приращение 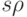 ) и посмотреть, что от него изменится; а затем устремить
) и посмотреть, что от него изменится; а затем устремить  (то есть длину вектора приращения) к нулю. В результате получится результат об исходных функциях; единственное, за чем нужно следить — это за тем, какие предположения о непрерывности и дифференцируемости использовались по дороге.
(то есть длину вектора приращения) к нулю. В результате получится результат об исходных функциях; единственное, за чем нужно следить — это за тем, какие предположения о непрерывности и дифференцируемости использовались по дороге.
Рациональность
Давайте применим теорему Вильямса в контексте, обобщающем теорему 7.1. Мы бы хотели создавать рациональные механизмы. Посмотрим, когда это получится.
Теорема 7.5. Рассмотрим проблему социального выбора с квазилинейными предпочтениями. Предположим, что множества типов 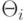 представляют собой интервалы:
представляют собой интервалы: ![\Theta_i = [\underline{\theta}_i, \overline{\theta}_i]](/sites/default/files/tex_cache/d0ada680778fe44fe4833e9413567223.png) . Тогда в предположениях теоремы 7.3 минимальная субсидия, которая требуется рациональному, правдивому и эффективному механизму, равна
. Тогда в предположениях теоремы 7.3 минимальная субсидия, которая требуется рациональному, правдивому и эффективному механизму, равна
![\min\left\{0, -(N-1)\mathbf E_\mathbf\theta\left[\sum\limits_{i=1}^Nv_i(a(\mathbf\theta),\theta_i)\right] + \sum\limits_{i=1}^NU_i(\underline{\theta}_i)\right\}.](/sites/default/files/tex_cache/85c803f347ce631a1768bff86df74cb5.png)
Значит, рациональные, правдивые и эффективные механизмы со сбалансированным бюджетом существуют тогда и только тогда, когда
![(N-1)\mathbf E_\mathbf\theta\left[\sum\limits_{i=1}^Nv_i(a(\mathbf\theta),\theta_i)\right] \le \sum\limits_{i=1}^NU_i(\underline{\theta}_i).](/sites/default/files/tex_cache/e1ba447969dcfc07620c8e71ba38f6fd.png)
Доказательство. По теореме Вильямса, достаточно рассмотреть механизмы VCG. Для них ожидаемая сумма трансферов
![\mathbf E_\mathbf\theta\left[\sum\limits_{i=1}^Np_i(\mathbf\theta)\right] = -\mathbf E_\mathbf\theta\left[\sum\limits_{i=1}^N\sum\limits_{j\neq i}v_j(a(\mathbf\theta),\theta_j)\right] + \sum\limits_{i=1}^Nk_i = \\ = -(N-1)\mathbf E_\mathbf\theta\left[\sum_{i=1}^Nv_i(a(\mathbf\theta),\theta_i)\right] + \sum\limits_{i=1}^Nk_i.](/sites/default/files/tex_cache/e645ee3a3a5b3aa48ada7bfb75f84145.png)
По рациональности, 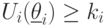 для всех
для всех  . Отсюда и получается утверждение теоремы.
. Отсюда и получается утверждение теоремы.
