Эффективные и оптимальные механизмы
Эффективные механизмы: VCG
Итак, мы научились максимизировать доход продавца. Теперь попытаемся решить более альтруистическую задачу: максимизируем общественное благосостояние (social welfare). Это значит, что мы будем пытаться распределить вещь тому, кому она больше всего нравится.
Мы уже знаем, что аукцион второй цены (без резервной цены) эффективен. А вот, например, оптимальный аукцион, который мы только что рассматривали, может оказаться и неэффективным. Во-первых, резервная цена автоматически предполагает, что иногда объект никому не достанется, даже если есть положительные ставки. Во-вторых, максимизируется виртуальная ценность: если распределения несимметричные, то это вовсе не эквивалентно максимизации самих  .
.
История создания эффективных механизмов восходит к самым истокам теории экономических механизмов. Собственно, мотивацией первой работы Уильяма Викри стал именно поиск эффективного (и правдивого) механизма: его аукцион второй цены, предложенный в [76], стал первым примером нетривиального дизайна экономических механизмов и фактически основал науку, которой мы сейчас занимаемся. Затем Кларк обобщил идею Викри и применил аналогичный механизм в контексте распределения вещей общего пользования (так называемых public goods) [13]. Наконец, в своем современном виде эффективные механизмы, которые мы сейчас будем рассматривать, появляются у Т.Гровса [24].
Для начала немного обобщим постановку задачи. Расширим возможные значения ценностей агентов, то есть обобщим 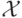 : теперь значения ценностей агентов будут
: теперь значения ценностей агентов будут ![x_i\in[\alpha_i,\omega_i]](/sites/default/files/tex_cache/64b0829cb068b4792611468343f94bb0.png) . Это нужно для того, чтобы разрешить отрицательные ценности. Напоминаем, что, по определению 5.1, функция распределения
. Это нужно для того, чтобы разрешить отрицательные ценности. Напоминаем, что, по определению 5.1, функция распределения 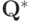 называется эффективной }, если она максимизирует общественное благосостояние, то есть
называется эффективной }, если она максимизирует общественное благосостояние, то есть
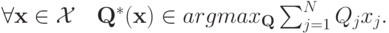
Проще говоря, мы даем вещь агенту с максимальной ценностью, либо одному из таких агентов, если их несколько. Введем теперь еще одно обозначение — если 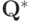 уже эффективна, то мы обозначим через
уже эффективна, то мы обозначим через  значение этого самого общественного благосостояния. Суммарное благосостояние всех агентов мы обозначим через
значение этого самого общественного благосостояния. Суммарное благосостояние всех агентов мы обозначим через
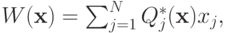
а суммарное благосостояние всех агентов без  -го — через
-го — через

Теперь можно переходить к определению.
Определение 5.3. Механизм Викри-Кларка-Гровса, он же механизм VCG (Vickrey-Clarke-Groves) — это эффективный механизм с правилом платежа 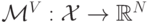 , определенным следующим образом:
, определенным следующим образом:
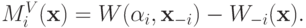
Напомним, что слово эффективный в определении означает, что правило распределения  уже задано:
уже задано:

Рассмотрим повнимательнее функцию платы  . Цена
. Цена 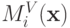 , которую придется заплатить агенту
, которую придется заплатить агенту  — это разница между общественным благосостоянием при наименьшей возможной ставке агента
— это разница между общественным благосостоянием при наименьшей возможной ставке агента  и благосостоянием всех остальных агентов при текущей ставке. То есть агент должен заплатить ровно столько, насколько он суммарно сделал хуже другим от того, что сделал ставку, а не ограничился минимумом (как правило, равносильным неучастию). В контексте аукционов
и благосостоянием всех остальных агентов при текущей ставке. То есть агент должен заплатить ровно столько, насколько он суммарно сделал хуже другим от того, что сделал ставку, а не ограничился минимумом (как правило, равносильным неучастию). В контексте аукционов 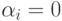 , и получается в точности аукцион второй цены.
, и получается в точности аукцион второй цены.
Если другие агенты делают ставки 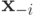 , то прибыль агента
, то прибыль агента  от ставки
от ставки 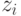 вычисляется как
вычисляется как
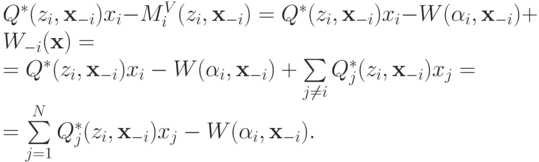
Здесь 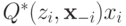 — ожидание дохода агента, а
— ожидание дохода агента, а 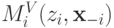 — ожидание выплаты агента. Вычитаемое от
— ожидание выплаты агента. Вычитаемое от  не зависит, а уменьшаемое по определению
не зависит, а уменьшаемое по определению 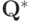 максимизируется, когда
максимизируется, когда  говорит правду. Значит, аукцион VCG правдив.
говорит правду. Значит, аукцион VCG правдив.
Из лекции "Теорема об эквивалентности доходности" мы знаем уже много свойств правдивых механизмов. В частности, ожидаемая доходность
![U^V_i(x_i)=\mathbf E[W(x_i,\mathbf X_{-i}) - W(\alpha_i,\mathbf X_{-i})]](/sites/default/files/tex_cache/69d6e595153339e4de5cd86784d2b20e.png)
будет возрастающей и выпуклой функцией. Но 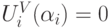 ; значит, по монотонности, мы получаем, что VCG рационален.
; значит, по монотонности, мы получаем, что VCG рационален.
Пусть есть другой механизм, который тоже эффективен, правдив и рационален. Тогда, по принципу эквивалентности доходности, его доходность 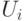 отличается от
отличается от 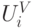 на константу. Но если
на константу. Но если

то механизм не будет рациональным (у агента  с ценностью
с ценностью 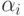 — отрицательная ожидаемая доходность). Значит,
— отрицательная ожидаемая доходность). Значит, 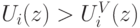 , то есть другой механизм больше дает агентам; при одинаковом распределении
, то есть другой механизм больше дает агентам; при одинаковом распределении 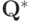 это значит, что агенты платят меньше. Таким образом, мы доказали следующую теорему.
это значит, что агенты платят меньше. Таким образом, мы доказали следующую теорему.
Теорема 5.2. Среди всех механизмов, которые распределяют один объект и являются эффективными, правдивыми и рациональными, механизм VCG максимизирует ожидаемые выплаты каждого агента.
На самом деле, даже максимизируя выплаты, VCG все равно не может добиться того, чтобы баланс сходился, то есть сумма выплат всех агентов равнялась нулю. В следующем параграфе мы рассмотрим другой механизм, в котором баланс будет сходиться, но не будет рациональности.
Кроме того, нужно понимать, что механизм VCG при всех своих замечательных свойствах может оказаться совершенно нереалистичен. Для вычисления функции распределения  в механизме VCG приходится решать сложную задачу оптимизации. Если агентов достаточно много, это не всегда можно сделать быстро: задача распределения в ряде ситуаций оказывается NP-трудной, в том числе "совсем" NP-трудной, то есть такой, к оптимальному решению которой даже приблизиться NP-трудно. Задача сделать вычислительно эффективный механизм, то есть механизм, который бы работал полиномиально долго и при этом обладал хорошими свойствами, — это совсем другая задача, в рамках классической теории экономических механизмов удовлетворительно не решенная. Пути ее решения были исследованы только в совсем недавних работах Нисана и Ронена [63]; мы в этом курсе рассматривать их не будем и, возможно, вернемся к ним позже. Совершенно аналогично нелегко сделать и эффективный оптимальный механизм.
в механизме VCG приходится решать сложную задачу оптимизации. Если агентов достаточно много, это не всегда можно сделать быстро: задача распределения в ряде ситуаций оказывается NP-трудной, в том числе "совсем" NP-трудной, то есть такой, к оптимальному решению которой даже приблизиться NP-трудно. Задача сделать вычислительно эффективный механизм, то есть механизм, который бы работал полиномиально долго и при этом обладал хорошими свойствами, — это совсем другая задача, в рамках классической теории экономических механизмов удовлетворительно не решенная. Пути ее решения были исследованы только в совсем недавних работах Нисана и Ронена [63]; мы в этом курсе рассматривать их не будем и, возможно, вернемся к ним позже. Совершенно аналогично нелегко сделать и эффективный оптимальный механизм.
Баланс бюджета и механизм AGV
Механизм VCG позволяет построить эффективную функцию распределения, максимизирующую всеобщее благосостояние. Это весьма общая конструкция, которая может быть применена далеко не только для ситуации аукциона. Но это еще не все, что можно потребовать от хорошего механизма.
Зачастую в задачах дизайна механизмов требуется, чтобы у механизма в результате его деятельности сходился баланс (budget balance property). Это значит, что система "замкнута": деньги перераспределяются между агентами, но никаких вливаний снаружи не требуется (и наружу никаких лишних денег не отдается).
Определение 5.4. Механизм 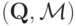 удовлетворяет условию сбалансированности бюджета, если
удовлетворяет условию сбалансированности бюджета, если
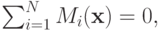
то есть сумма выплат всех агентов равна нулю.
Условие сбалансированности бюджета требуется нередко, но механизм VCG в том виде, в котором мы его рассмотрели в предыдущем параграфе, свойства этого не обеспечивает (см., например, раздел 7.2). А нам хотелось бы построить механизм, который и эффективен был бы, и бюджет соблюдал бы нулевой. Эту задачу исполняет механизм AGV, или механизм Эрроу-д'Аспремона-Жерар-Варе (Arrow-d'Aspremont-Gerard-Varet). Как и в случае VCG, это не совместная работа, а две разных, независимых и вышедших в одно время: Эрроу [5] и остальных авторов [16]. Обращаем внимание читателя на то, что "других авторов" не три, а два: Жерар-Варе — это один человек.
Этот механизм тоже эффективен (то есть использует правило распределения 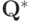 ). Его выплаты
). Его выплаты 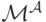 определяются как
определяются как
![M_i^{\mathcal A}(\mathbf x)=\frac1{N-1}\sum_{j\neq i}\mathbf E_{\mathbf X_{-j}}[W_{-j}(x_j,\mathbf X_{-j})]-\mathbf E_{\mathbf X_{-i}}[W_{-i}(x_i,\mathbf X_{-i})].](/sites/default/files/tex_cache/a7634be45356b84ab2383ec54402a2a0.png)
"Физический смысл" похож на смысл аукциона VCG: можно сказать, что каждый агент компенсирует каждому другому агенту свое присутствие на аукционе. При таких выплатах очевидно, что баланс механизма AGV сходится, поскольку каждое ожидание входит в сумму один раз с плюсом и один раз с минусом:
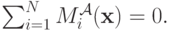
Для полного счастья осталось лишь показать, что механизм AGV правдив и рационален. И здесь нас ждет некоторое разочарование. Во-первых, в доминантных стратегиях доказать правдивость не получится. Но равновесие по Нэшу (и даже по Байесу-Нэшу) получится: если другие агенты говорят правду, то есть сообщают 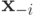 , а агент
, а агент  делает ставку
делает ставку 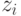 , его ожидаемый итоговый доход равен
, его ожидаемый итоговый доход равен
![\mathbf E_{\mathbf X_{-i}}\left[Q^*_i(z_i,\mathbf X_{-i}) - M_i^{\mathcal A}(\mathbf x)\right] = \mathbf E_{\mathbf X_{-i}}[Q^*_i(z_i,\mathbf X_{-i}) + W_{-i}(z_i,\mathbf X_{-i})] - \\ -\mathbf E_{\mathbf X_{-i}}\left[\frac1{N-1}\sum\limits_{j\neq i}\mathbf E_{\mathbf X_{-j}}[W_{-j}(X_j,\mathbf X_{-j})]\right].](/sites/default/files/tex_cache/0a852dc1b709b5933342210fdd01513f.png)
Первое слагаемое 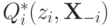 — доход агента, из которого вычитается выплата агента. Вычитаемое ожидание не зависит от
— доход агента, из которого вычитается выплата агента. Вычитаемое ожидание не зависит от 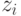 , а первое ожидание максимизируется при
, а первое ожидание максимизируется при 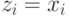 , поэтому по Нэшу и по Байесу-Нэшу механизм действительно правдив.
, поэтому по Нэшу и по Байесу-Нэшу механизм действительно правдив.
А вот рациональности у механизма AGV, вообще говоря, не будет.
Пример 5.4. Рассмотрим ситуацию торговли с двумя участниками, которую мы будем подробно обсуждать в разделе
"Двусторонняя торговля и теорема Вильямса"
. В ней участвуют два игрока, один из которых хочет продать вещь, другой — купить. Они должны договориться о цене, подавая механизму свои себестоимость и максимальную приемлемую цену  соответственно. Механизм должен решить, происходит ли обмен, и если да, то сколько платит покупатель и сколько получает продавец.
соответственно. Механизм должен решить, происходит ли обмен, и если да, то сколько платит покупатель и сколько получает продавец.
Предположим, что мы пытаемся реализовать механизм AGV в этой ситуации. Эффективность означает, что товар перераспределяется тогда и только тогда, когда 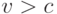 . Выплата покупателя будет равна
. Выплата покупателя будет равна
![M_v^{\mathcal A}(c,v) = \mathbf E_{v}[W_{v}(c,v)] - \mathbf E_{c}[W_{c}(c,v)],](/sites/default/files/tex_cache/7f376c798067c6c8bc814b1c53cb9842.png)
а продавца —
![M_c^{\mathcal A}(c,v) = \mathbf E_{c}[W_{c}(c,v)] - \mathbf E_{v}[W_{v}(c,v)],](/sites/default/files/tex_cache/4e7ad3ddd872da5013096176d77c50a9.png)
где 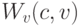 — благосостояние покупателя,
— благосостояние покупателя, 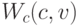 — благосостояние продавца. Предположим, что они равны
— благосостояние продавца. Предположим, что они равны
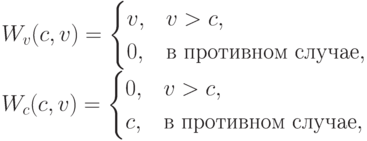
то есть покупатель может увеличить свое благосостояние в случае покупки, а продавец может остаться при своей вещи (это логично: покупатель должен как раз взносом компенсировать продавцу уменьшение его благосостояния на эту вещь). При этом суммарное благосостояние, разумеется, максимизируется в эффективном случае. Предположим, что  и
и  распределены равномерно на
распределены равномерно на ![[v_0,v_1]](/sites/default/files/tex_cache/7a1ee6583b1b56693e7560c6c710d432.png) и
и ![[c_0,c_1]](/sites/default/files/tex_cache/0de636b1db4afe835aab9358cbdc5453.png) соответственно. Будем предполагать, что
соответственно. Будем предполагать, что  и
и 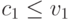 , потому что вне этих условий все равно никакой торговли точно не случится. Тогда
, потому что вне этих условий все равно никакой торговли точно не случится. Тогда
![\mathbf E_{c}[W_{c}(c,v)] &=& \int_{c_0}^{c_1}\frac{W_{c}(c,v)}{c_1-c_0}dc =
c\frac{c_1 - \min\{v,c_1\}}{c_1-c_0}, \\
\mathbf E_{v}[W_{v}(c,v)] &=& \int_{v_0}^{v_1}\frac{W_{v}(c,v)}{v_1-v_0}dv =
v\frac{v_1 - \max\{c,v_0\}}{v_1-v_0}.](/sites/default/files/tex_cache/62249b9ed3f6945a8063c2a9d32bc5c0.png)
Пока все логично: ожидаемое благосостояние покупателя с ценностью  — это
— это  умножить на долю случаев, когда продажа происходит; с благосостоянием продавца то же самое. Но давайте теперь посмотрим на выплату покупателя (и, соответственно, доход продавца):
умножить на долю случаев, когда продажа происходит; с благосостоянием продавца то же самое. Но давайте теперь посмотрим на выплату покупателя (и, соответственно, доход продавца):
![M_v^{\mathcal A}(c,v) = -M_c^{\mathcal A}(c,v) = \mathbf E_{v}[W_{v}(c,v)] - \mathbf E_{c}[W_{c}(c,v)] = \\
=v\frac{v_1 - \max\{c,v_0\}}{v_1-v_0} - c\frac{c_1 - \min\{v,c_1\}}{c_1-c_0}.](/sites/default/files/tex_cache/8d0e7563754106d594f84d7d6180eb49.png)
Конечно, когда 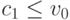 , сделка происходит всегда, выплата покупателя всегда равна
, сделка происходит всегда, выплата покупателя всегда равна  , его доход, соответственно, равен
, его доход, соответственно, равен  , доход продавца равен
, доход продавца равен  , и все довольны (хоть это и не очень честно по отношению к покупателю, но все-таки рационально). А что, если
, и все довольны (хоть это и не очень честно по отношению к покупателю, но все-таки рационально). А что, если  ? В такой ситуации
? В такой ситуации 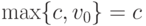 ,
, 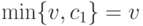 , и выплата равна
, и выплата равна
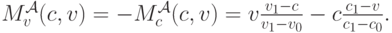
Легко убедиться, что она может оказаться не равной нулю — например, для ![[v_0,v_1]=[1,3]](/sites/default/files/tex_cache/8de279e48938dd7d80ecbafcee19a8ff.png) ,
, ![[c_0,c_1]=[0,2]](/sites/default/files/tex_cache/58e6157636192da1d05eac6399488515.png) ,
, 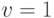 ,
, 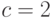 получается
получается 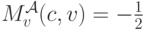 и, соответственно,
и, соответственно, 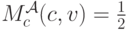 . В такой ситуации никакой торговли не происходит, но продавцу приходится доплатить покупателю просто за участие в аукционе! Разумеется, такой аукцион для продавца нерационален.
. В такой ситуации никакой торговли не происходит, но продавцу приходится доплатить покупателю просто за участие в аукционе! Разумеется, такой аукцион для продавца нерационален.
Конец примера 5.4.
Интересно, почему в данной ситуации не получается добиться рациональности? Оказывается, что это не механизм плохой; есть более глубокая причина того, почему "совсем замечательный" механизм не построить.
Теорема 5.3. (д'Аспремона-Жерар-Варе) Эффективный, правдивый (в доминантных стратегиях) и рациональный механизм, у которого сходится баланс, существует тогда и только тогда, когда механизм VCG дает положительную ожидаемую прибыль аукционеру.
Доказательство. В одну сторону доказательство тривиально: VCG должен давать прибыль, потому что он, как мы видели раньше, дает аукционеру максимальную ожидаемую прибыль из всех эффективных правдивых рациональных механизмов (а все остальные ему эквивалентны по теореме об эквивалентности доходности). Это тривиальное замечание и есть та проблема, из-за которой не всегда получается построить хороший механизм, ведь VCG, как мы увидим в разделе 7.2, порой требует внешних вливаний.
Докажем, однако, и в другую сторону: предъявим конструкцию эффективного правдивого рационального механизма со сходящимся балансом в том случае, когда VCG дает прибыль.
Возьмем за основу механизм AGV. Принцип эквивалентности доходности нам говорит: есть такие константы 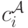 , что ожидаемая доходность
, что ожидаемая доходность
![U^{\mathcal A}_i(x_i) = \mathbf E[W(x_i,\mathbf X_{-i})]-c^{\mathcal A}_i.](/sites/default/files/tex_cache/3d3ed5296af746e643723b652abb838f.png)
Для VCG это тоже верно: существуют такие константы 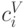 , что
, что
![U^V_i(x_i) = \mathbf E[W(x_i,\mathbf X_{-i})]-c^V_i.](/sites/default/files/tex_cache/1f6a3f9f0584d5f4a8a79590bbeb866f.png)
Однако механизм AGV пока что не является рациональным; чтобы добиться рациональности, слегка модифицируем его. Дано, что VCG приносит прибыль:
![\mathbf E\left[\sum\limits_{i=1}^NM^V_i(\mathbf X)\right]\ge 0.](/sites/default/files/tex_cache/b16d1f1b9a02f3cd26028b11e5bb7968.png)
Поскольку AGV по определению имеет сходящийся баланс, то его ожидание прибыли равно нулю:
![\mathbf E\left[\sum\limits_{i=1}^NM^V_i(\mathbf X)\right]\ge \mathbf E\left[\sum\limits_{i=1}^NM^{\mathcal A}_i(\mathbf X)\right]=0.](/sites/default/files/tex_cache/aae514f8d3911b942d3f162d6d19f22a.png)
Или, в терминах наших констант,
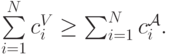
Введем теперь специальные поправки: для 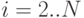
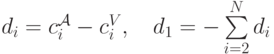
( 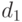 просто выбирается таким образом, чтобы сумма всех
просто выбирается таким образом, чтобы сумма всех 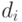 оказалась равна нулю).
оказалась равна нулю).
Тогда искомым механизмом будет механизм AGV с нашими поправками:
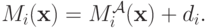
Очевидно, баланс все так же сходится (поскольку это 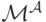 , подправленный на константы, которые в сумме дают
, подправленный на константы, которые в сумме дают  ). Механизм правдивый, потому что выплаты агента отличаются от выплат правдивого
). Механизм правдивый, потому что выплаты агента отличаются от выплат правдивого 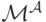 на константу.
на константу.
Осталось только проверить, что он рациональный, то есть ожидание дохода каждого агента больше нуля. Для 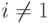
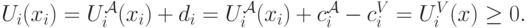
Для первого агента все то же самое, нужно только заметить, что

так как общая сумма 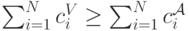 .
.
Таким образом, мы сделали такой эффективный правдивый рациональный механизм, у которого сходится баланс. Иначе говоря, выплаты остаются между агентами, участвующими в аукционе, но ни один из них не ожидает остаться в убытке.
