Теория игр
Совместные смешанные стратегии
Мы уже говорили о том, что в игре может быть несколько равновесий Нэша. Давайте приведем конкретный пример; пример не только проиллюстрирует этот факт, но и вдобавок поднимет важную проблему, которую мы попытаемся решить в этом параграфе.
Пример 1.9. Этот классический пример называется "Семейный спор" (по-английски звучит более внушительно: "Battle of the sexes"). Рассмотрим семью (пока что из двух человек), которая пытается решить, куда пойти вечером. Муж, разумеется, хочет идти на футбол, в то время как жена пытается вытащить мужа в театр. Но, несмотря на этот конфликт интересов, за семью можно быть спокойным: и муж, и жена хотят провести вечер вместе, и ни футбол, ни театр будут не в радость, если пойти туда одному. Осталось только сделать предположение (пожалуй, самое противоестественное), что муж и жена не обсуждают друг с другом свои решения, а просто сами по себе идут или на футбол, или в театр. У игры получается следующая матрица (строки выбирает муж, столбцы — жена; в векторе результатов первый компонент принадлежит мужу, второй — жене).
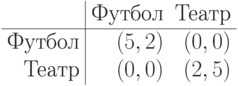
Как нетрудно заметить, у этой игры два равновесия Нэша:
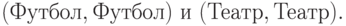
Ни мужу, ни жене невыгодно отклоняться от одного из этих равновесий. Но вот первая беда: любое из них нечестное — если постоянно выбирать одну и ту же стратегию (а стимулов отклоняться-то нет), один супруг будет получать значительно большую выгоду, чем другой.
Можно попробовать решить эту игру в смешанных стратегиях. Сыграем за мужа: найдем для данной вероятности  того, что жена пойдет на футбол, оптимальную вероятность
того, что жена пойдет на футбол, оптимальную вероятность  пойти на футбол самому:
пойти на футбол самому:
![\text{E [выгода мужа]} = 5pq + 2(1-p)(1-q) = p(7q-2) + 2-2q.](/sites/default/files/tex_cache/a9ad5f64fde13214754fa072d28480e0.png)
Поскольку для жены ситуация абсолютно симметрична, понятно, что в точке  ,
, 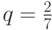 (каждый выбирает свой любимый способ провести вечер с вероятностью
(каждый выбирает свой любимый способ провести вечер с вероятностью  ) достигается равновесие в смешанных стратегиях, ведь ожидаемая выгода каждого участника не зависит от его стратегии. В итоге ожидаемая выгода и мужа, и жены оказывается равной
) достигается равновесие в смешанных стратегиях, ведь ожидаемая выгода каждого участника не зависит от его стратегии. В итоге ожидаемая выгода и мужа, и жены оказывается равной 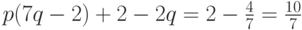 . Вот и вторая беда: использовать смешанные стратегии хуже, чем просто согласиться на "неподходящий" вариант: там выгода будет равна
. Вот и вторая беда: использовать смешанные стратегии хуже, чем просто согласиться на "неподходящий" вариант: там выгода будет равна  , а тут всего
, а тут всего 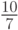 .
.
Конец примера 1.9.
На первый взгляд кажется, что делать нечего: придется кому-то поступиться своим интересом. Решение приходит в виде нового понятия равновесия, которое позволяет участникам использовать внешнюю информацию.
Определение 1.7. Совместная смешанная стратегия игроков — это распределение вероятностей на всем множестве возможных чистых стратегий всех игроков 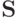 .
.
То есть, грубо говоря, муж и жена заранее договариваются: кто-то (возможно, кто-то третий — важно, что ни один участник не контролирует этот результат, но оба имеют к нему доступ) вечером подбросит монетку, и если выпадет орел, то они вместе пойдут в театр, а если решка — на футбол. В такой ситуации исход получается оптимальным: и точку 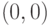 выбирать никогда не придется, и равновесие честное, ведь у каждого участника ожидаемая выгода равна
выбирать никогда не придется, и равновесие честное, ведь у каждого участника ожидаемая выгода равна  .
.
Определение 1.8. Равновесие в совместных смешанных стратегиях — это такое распределение вероятностей  на множестве чистых стратегий
на множестве чистых стратегий 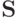 , что для всех
, что для всех 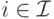 и любой пары векторов
и любой пары векторов 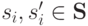

или, что то же самое,
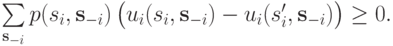
То есть некое внешнее устройство выбирает стратегию 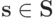 случайным образом по распределению
случайным образом по распределению  , и оказывается так, что для каждого из игроков в получившемся векторе невыгодно отклоняться от своей стратегии. В примере с семейным спором все выходит именно так: монетка определяет стратегию и мужа, и жены, но при этом выбор делается между двумя равновесиями Нэша, то есть любой случайно выбранный вектор получится равновесным. Совместные смешанные стратегии — это способ перейти от одного равновесия Нэша к линейной комбинации нескольких равновесий, если эта комбинация оказывается более выгодна агентам.
, и оказывается так, что для каждого из игроков в получившемся векторе невыгодно отклоняться от своей стратегии. В примере с семейным спором все выходит именно так: монетка определяет стратегию и мужа, и жены, но при этом выбор делается между двумя равновесиями Нэша, то есть любой случайно выбранный вектор получится равновесным. Совместные смешанные стратегии — это способ перейти от одного равновесия Нэша к линейной комбинации нескольких равновесий, если эта комбинация оказывается более выгодна агентам.
Равновесия по Байесу-Нэшу
До сих пор мы рассматривали исключительно игры, в которых все агенты знали все на свете. Каждый агент знал функции выплаты 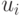 других агентов, знал множества стратегий других игроков
других агентов, знал множества стратегий других игроков 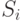 . Более того, каждый агент знал, что каждый другой агент это знает, и что каждый другой агент знает, что он знает, что... в общем, понятно.
. Более того, каждый агент знал, что каждый другой агент это знает, и что каждый другой агент знает, что он знает, что... в общем, понятно.
Однако на самом деле это условие довольно часто не выполняется. А если агент не знает, к примеру, какие выплаты у других агентов, то говорить о равновесии Нэша становится бессмысленным. Что же делать?
Пример 1.10. В качестве примера рассмотрим вариант все того же "семейного спора", который на этот раз для мужа гораздо печальнее. Предположим, что муж не уверен, хочет ли жена провести с ним вечер или, наоборот, в этот раз от него отдохнуть. Если жена ищет встречи, то матрица игры будет как в примере 1.9:
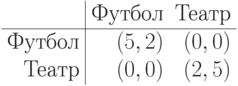
А если встречаться не хочет, то матрица становится другой:
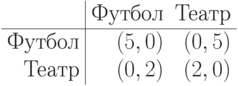
Пусть муж ничего не знает о желаниях жены, и для него вероятности этих исходов равны 50%. Таким образом, с точки зрения мужа, у жены есть два возможных типа; или, что то же самое, есть два возможных равновероятных состояния мира, и только жена знает истинное состояние (этакая, простите за выражение, "жена Шредингера").
Если в такой ситуации муж решит пойти на футбол, то (в предположении о 50%) ему невыгодно будет менять свое предпочтение, ведь в случае футбола выгода получается 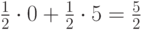 , а в случае театра лишь
, а в случае театра лишь  . А для жены, очевидно, в такой ситуации выгодным будет идти на футбол, если она хочет встретить мужа, и идти в театр, если не хочет. Таким образом, профиль стратегий
. А для жены, очевидно, в такой ситуации выгодным будет идти на футбол, если она хочет встретить мужа, и идти в театр, если не хочет. Таким образом, профиль стратегий ![(\text{Футбол}, [\text{Футбол}, \text{Театр}])](/sites/default/files/tex_cache/a4bc21c1a6d7da04128d927572c6d7dd.png) будет находиться в равновесии Нэша.
будет находиться в равновесии Нэша.
Конец примера 1.10.
Более общая формулировка будет изрядно напоминать равновесие в совместных смешанных стратегиях. Но теперь придется немного дополнить модель самой игры. Определение 1.9 отличается от определения 1.1 только множествами типов  .
.
Определение 1.9. Стратегическая игра с неполной информацией — это четверка

где обозначения расшифровываются следующим образом:
-
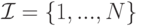 — конечное множество игроков.
— конечное множество игроков. -
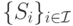 — множество доступных игрокам действий.
— множество доступных игрокам действий. -
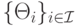 — множество типов игроков; для типов мы будем применять ту же нотацию, например
— множество типов игроков; для типов мы будем применять ту же нотацию, например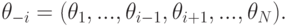
Через
 будем обозначать множество векторов типов:
будем обозначать множество векторов типов:  . Каждому игроку
. Каждому игроку  известен его собственный тип
известен его собственный тип 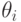 и общее распределение
и общее распределение  , из которого берутся типы всех остальных; в частности, игрок
, из которого берутся типы всех остальных; в частности, игрок  знает
знает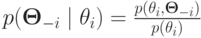 .
. -
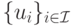 — множество функций выплат
— множество функций выплат 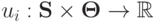 . Функции выплат теперь зависят не только от стратегий, но и от типов.
. Функции выплат теперь зависят не только от стратегий, но и от типов.
В играх с неполной информацией игроки не знают типов других игроков, но знают распределение. Таким образом, легко определить новое понятие равновесия, которое теперь будет действовать только в ожидании.
Определение 1.10. Равновесие по Байесу-Нэшу для стратегической игры с неполной информацией 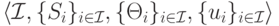 — это такой профиль стратегий
— это такой профиль стратегий 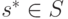 , что для всякого агента
, что для всякого агента 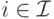 и всякого его типа
и всякого его типа 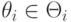 выполняется следующее условие:
выполняется следующее условие:

Очевидно (проверьте!), что любое равновесие в доминантных стратегиях является равновесием по Байесу-Нэшу.
Кроме уже описанных, нам в теории экономических механизмов потребуется и еще одно понятие равновесия, промежуточное между равновесием по Байесу-Нэшу и равновесием в доминантных стратегиях.
Определение 1.11. Равновесие ex post для стратегической игры с неполной информацией 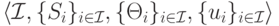 — это равновесие по Байесу-Нэшу
— это равновесие по Байесу-Нэшу 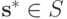 , в котором дополнительно выполняется следующее условие: для всех
, в котором дополнительно выполняется следующее условие: для всех 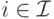 , всех
, всех 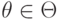 и всех
и всех 

Проще говоря, даже если агенту  рассказать о том, какие типы были у всех остальных игроков, ему все равно не будет резона менять свое решение. Поэтому агенту
рассказать о том, какие типы были у всех остальных игроков, ему все равно не будет резона менять свое решение. Поэтому агенту  гарантированно "не о чем жалеть" в результате игры: даже если он узнает то, чего не знал раньше, все равно для него
гарантированно "не о чем жалеть" в результате игры: даже если он узнает то, чего не знал раньше, все равно для него 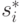 останется оптимальной стратегией. Мы еще не раз встретимся с понятием ex post и другими моментами времени в течение игры в контексте аукционов; подробно эти понятия мы объясним в
"Введение в дизайн механизмов"
.
останется оптимальной стратегией. Мы еще не раз встретимся с понятием ex post и другими моментами времени в течение игры в контексте аукционов; подробно эти понятия мы объясним в
"Введение в дизайн механизмов"
.
