Функциональное программирование
9.4. Вспомогательные функции
9.4.1. Составные функции
Как отмечает П. Веллин и др. [14, с. 96], левая часть составных функций задаётся так же, как и левая часть любых пользовательских функций. Правая часть содержит заключённую в круглые скобки последовательность разделённых точкой с запятой выражений:
funcname[arg1_,arg2_,...]:=(expr1,expr2,...)
Составные функции очень похоже на суперпозицию функций, однако аргументами одних выражений не обязательно должны быть результаты других входящих в составную функцию выражений. Когда подаётся команда на вычисление составной функции некоторого аргумента, то выражения, указанные в правой части, вычисляются по очереди, и результатом функции является результат вычисления последнего выражения.
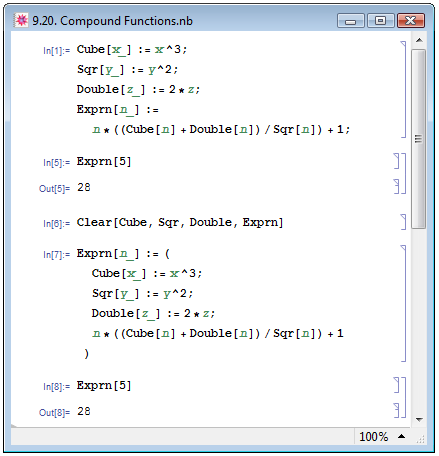
В примере In[1] на рис. 9.20 мы последовательно задаём функции возведения некоторого выражения в куб Cube, квадрат Sqr и удвоения выражения Double, и только затем определяем функцию Exprn, осуществляющую с аргументом  следующий набор действий:
следующий набор действий:  . В примере In[5] мы применяем функцию Exprn к числу 5.
. В примере In[5] мы применяем функцию Exprn к числу 5.
Теперь зададим составную функцию с тем же заголовком Exprn, выполняющую весь описанный набор действий. В In[6] на рис. 9.20 для наглядности мы очищаем выражения Cube, Sqr, Double и Exprn. В примере In[7] мы сразу же задаём функцию Exprn, обращение к которой даёт нам требуемый результат. Функции для получения промежуточных выражений мы включаем непосредственно в тело Exprn. В примере In[8] мы применяем вновь заданную нами функцию Exprn к числу 5: результаты в Out[5] и Out[8] полностью идентичны.
П. Веллин и др. [14, с. 96] акцентирует внимание на следующих моментах, связанных с составными функциями.
Поскольку выражения в правой части вычисляются в заданном порядке, требуемые значения должны быть присвоены, а пользовательские функции определены до обращения к ним. Имена аргументов пользовательский функций должны быть отличными от имён аргументов составной функции (так в примере In[7] на рис. 9.20 аргументом составной функции Exprn мы выбрали символ n, а аргументами содержащихся в её теле пользовательских функций — символы x, y и z).
Когда мы задаём составную функцию, вместе с ней (в её теле) мы также определяем другие пользовательские функции и значения переменных. Если мы удалим заданную нами составную функцию, например, при помощи Clear, то определённые в её теле пользовательские функции и значения переменных сохранятся. В связи с этим, при дальнейших расчётах могут возникнуть проблемы, если мы снова захотим воспользоваться переменными или выражениями, которые являются заголовками этих функций.
В программистской практике является плохим тоном оставлять вспомогательные функции, в использовании которых однозначно не будет необходимости в дальнейших вычислениях.
9.4.2. Локализация имён: функция Module
П. Веллин и др. [14, с. 98] пишет, что для того, чтобы пользовательские функции, заданные в теле составной функции, были изолированы от остального текста программы, то есть, обращение к их заголовкам не приводило бы к выполнению какого-либо набора действий, к правой части составной функции применяется функция Module:
funcname[arg1_,arg2_,...]:=Module[{name1,name2=val,...},exprs]
Первый аргумент функции Module — список имён функций или переменных, которые мы хотим локализовать, то есть, сделать так, чтобы они рассматривались в заданном виде только в пределах функции funcname. Второй аргумент — exprs — включает все выражения, которые требуется задать.
Проиллюстрируем действие функции Module в примерах на рис. 9.21.
В примере In[1] мы вновь задали функцию Exprn точно таким же способом, что и в примере In[7] на рис. 9.20. В In[2] мы списком вывели результат действия на число 5 функций Exprn, Cube, Sqr и Double: в Out[2] мы получили список численных значений соответствующих функций. В примере In[3] мы очистили заголовок функции Exprn. В примере In[4] мы осуществили то же действие, что и в In[2]: в списке Out[4] элемент, соответствующий функции Exprn, принял неопределённое значение Exprn[5], остальные элементы так и остались числами.
Для чистоты демонстрации в In[5] освободим все выражения, использованные ранее в качестве заголовков пользовательских функций.
Теперь локализуем имя функции Cube в пределах функции Exprn. Для этого воспользуемся при задании Exprn функцией Module, указав первым её аргументом выражение Cube (пример In[6]). В In[7] мы снова вывели результат действия на число 5 вновь заданной функции Exprn, Cube, Sqr и Double: в списке Out[7] элемент, соответствующий функции Cube, не является числом, то есть, применённое вне пределов Exprn выражение Cube является просто символьным выражением. В In[8] мы очистили выражение Exprn, а в In[9] ещё раз вывели список: в Out[2] единственные элементы, обладающие численными значениями, соответствуют функциям Sqr и Double, поскольку только их мы не освободили от определённой ранее роли.
9.4.3. Локализация значений: функция Block
Пусть при проведении расчётов мы пользуемся некоторым выражением, которому присвоено строго определённое значение. Если на каком-то этапе вычислений возникла необходимость произвести расчёт с другим значением этого выражения, а в дальнейших вычислениях использовать прежнее его значение, П. Веллин и др. [14, с. 99] предлагает использовать функцию Block. Заданная в виде Block[{ex1=val1,ex2=val2,...},exprs] она вычисляет выражения exps при заданных в первом аргументе значениях val1,val2,... выражений ex1,ex2,…, при этом значения val1,val2,... принимаются выражениями лишь в пределах функции Block.
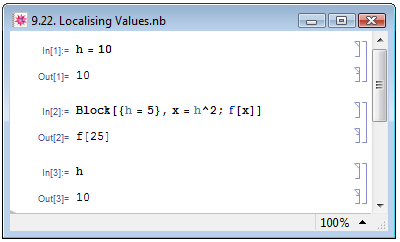
В примере In[1] на рис. 9.22 мы присвоили выражению h значение 10. В примере In[2] мы указали неопределённую функцию f[x], в которой x равняется h^2, и вычисления мы проводили при h равном 5. При этом мы воспользовались функцией Block для того, чтобы h равнялось 5 только при вычислении функции f[x]. В примере In[3] мы убеждаемся в том, что вне функции Block выражение h по-прежнему имеет значение 10.
9.4.4. Локализация констант: функция With
Согласно П. Веллину и др. [14, с. 99], функция With[{ex1=val1,ex2=val2,...},exprs] вместо входящих в exprs выражений ex1,ex2,... подставляет величины val1,val2,..., при этом за пределами функции With выражения ex1,ex2,... принимают отличные от val1,val2,... значения, заданные ранее.
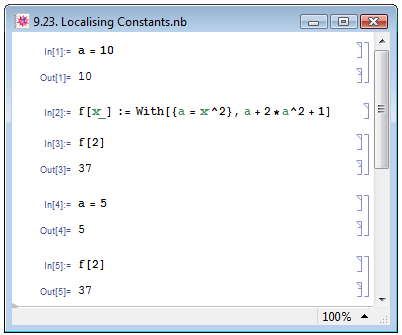
В примере In[1] на рис. 9.23 мы присвоили выражению a значение 10. В примере In[2] мы определили пользовательскую функцию, в левой части которой в качестве переменной значится символ x, а в правой — выражение, включающее только символ a: при этом при помощи функции With символ a мы заменили выражением x^2. В примере In[3] мы применили определённую нами в In[2] функцию к величине 2. В In[4] мы присвоили a новое значение 5, однако, на результате применения функции f это ни коим образом не отразилось — см. пример In[5].
Ключевые термины
Анонимной функцией называется компактная форма задания чистой функции, в которой вместо символов переменных используются специальные выражения Mathematica с заголовком Slot.
Вызовом вложенной функции называется последовательное применение к выражению нескольких функций.
Композиция (суперпозиция) функций — это применение одной функции к результату другой.
Функции — это объекты, которые после проведения манипуляций с полученными на входе выражениями, возвращают однозначно соответствующие им выражения на выходе.
Чистыми называются функции, которые используются только в момент их создания.
Краткие итоги
В данной лекции мы познакомились с основами функционального программирования на языке программирования Mathematica. В частности мы познакомились с встроенными функциями Mathematica, которые позволяют эффективно управлять другими выражениями. Мы научились сочетать функции, делая текст программы более компактным и последовательным. Мы научились задавать собственные функции, предназначенные как для многократного, так и для одиночного применения. Мы познакомились с методами задания функций, минимизирующими их влияние на остальной текст программы.
Вопросы
- Какими способами Mathematica позволяет применить заданную функцию func к некоторому выражению expr?
- Чем отличаются действия, оказываемые на выражения функциями Map и Apply? Какова полная и постфиксная форма этих функций?
- Какие функции Mathematica позволяют применять к элементам выражения функции нескольких аргументов? В каком виде задаются их аргументы?
- Что вносит атрибут Listable в действия, которые выполняют функции?
- Для каких целей используются функции Inner и Outer? Какие аргументы они имеют?
- Что такое суперпозиция функций? Каким образом Mathematica позволяет осуществлять суперпозицию функций?
- В каком виде в Mathematica задаются явные пользовательские функции?
- Что такое чистые функции? Каким образом они определяются в Mathematica?
- Что такое анонимные функции? Каким образом они определяются в Mathematica?
- Каким образом в Mathematica задаются составные функции? В чём состоит отличие составной функции от суперпозиции функций?
- Для каких целей в Mathematica применяются локализация имён, значений, констант при задании пользовательских функций? Посредством каких функций они осуществляются?
Упражнения
- Используя исходный вложенный список l1={{1,7},{8,3},{9,5},{7,5},{6,8},{5,6},{2,2}}, создайте одномерный список l2={8,11,14,12,14,11,4}, элементами которого являются суммы элементов второго уровня списка l1. Осуществите это двумя способами:
- при помощи функции Apply;
- при помощи встроенной функции Map и пользовательской функции, выполняющей суммирование требуемых элементов.
- Пользуясь функцией MapThread, получите транспонированную матрицу m2 из исходной m1, заданной списком m1={{a,b,c},{d,e,f},{g,h,i}}. Результат представьте в форме таблицы.
Создайте матрицу m3, заменив в матрице m2 при помощи подстановок каждый символ его порядковым номером в латинском алфавите.
Пользуясь функцией MapThread, получите вектор-столбец, элементами которого являются суммы элементов строк матрицы m3.
-
- Используя функцию Inner, создайте пользовательскую функцию divfield[field,coord], вычисляющую дивергенцию векторного поля, заданного вектором field={fx,fy,fz}, в трёхмерном декартовом пространстве; переменные по пространственным координатам заданы вектором coord={x,y,z}.
- Выполните усложнённое задание, которое даёт П. Веллин и др. в своей книге [14, с. 85]: создайте пользовательскую функцию, вычисляющую дивергенцию векторного поля field={f1,f2,...,fn} в n-мерном пространстве; переменные заданы вектором coord={c1,c2,...,cn}. Дивергенция в этом случае будет задаваться выражением df1/dc1+df2/dc2+...+dfn/dcn.
- Колода игральных карт есть множество, являющееся прямым произведением двух множеств. Первое множество — масти: пики (spears), черви (hearts), трефы (clubs) и бубны (diamonds). Второе множество — достоинств карт: туз (Ass), король (King), дама (Dame), валет (Jacket) и карты от 10 до 2. Выполните следующее задание, которое даёт Е. М. Воробьём в книге [1, с. 138]. С помощью функции Outer создайте вложенный список, элементами которого являются списки, содержащие по два элемента, первым из которых являются символы s, с, h или d, а вторым — символы А, К, D, J, 10,..., 2.
- Создайте пользовательскую функцию одного численного аргумента
 , которая
, которая
- извлекает кубический корень из
 ;
; - находит ближайшее к
 число, нацело делящееся на 3, и вычисляет произведение этого числа и
число, нацело делящееся на 3, и вычисляет произведение этого числа и  ;
; - создаёт двухмерный рисунок, содержащий случайным образом расположенные на плоскости круги единичного радиуса, количество которых равно
 ;
; - выводит на экран значение выражения
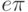 с точностью до
с точностью до  знаков после запятой;
знаков после запятой; - создаёт единичную матрицу размерностью argxarg и в табличном виде выводит её на экран;
- решает задачу Коши
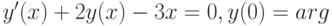 и визуализирует решение в пределах
и визуализирует решение в пределах  от
от  до
до  .
.
- извлекает кубический корень из
- Создайте пользовательскую функцию нескольких аргументов
 которая
которая
- находит аналитические решения квадратного уравнения
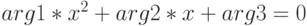 ;
; - выводит на экран изображение куба единичных размеров с координатами
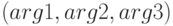 и сферы единичного радиуса с центром в точке
и сферы единичного радиуса с центром в точке  ; цвета куба и сферы должны определяться аргументами
; цвета куба и сферы должны определяться аргументами 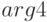 и
и 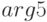 соответственно;
соответственно; - находит расстояние между двумя точками на плоскости, координаты которых заданы как
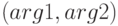 и
и 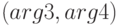 ;
; - находит сумму
 , если оба аргумента чётные, разность
, если оба аргумента чётные, разность  , если оба аргумента нечётные, произведение
, если оба аргумента нечётные, произведение  , если один из аргументов чётный, а другой — нечётный, и выдаёт сообщение "задайте другие аргументы", если ни одно из условий не выполняется;
, если один из аргументов чётный, а другой — нечётный, и выдаёт сообщение "задайте другие аргументы", если ни одно из условий не выполняется; - решает задачу Коши
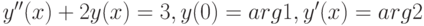 и визуализирует решение в пределах
и визуализирует решение в пределах  от
от 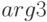 до
до 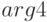 ;
; - дублирует действие встроенной функции Power[x,y]; Subtract[x,y]; Log[b,z].
- находит аналитические решения квадратного уравнения