Функциональное программирование
9.3. Определение пользовательских функций
9.3.1 Явные пользовательские функции
Функции — это объекты, которые после проведения манипуляций с полученными на входе выражениями, возвращают однозначно соответствующие им выражения на выходе. При этом манипуляции могут быть как простыми, в одно действие, так и сложными, в несколько шагов. В принципе, функции Mathematica мы можем расценивать так же, как и математические функции.
Теперь, пользуясь подходом Е. М. Воробьёва [1, с. 126–127], попробуем ответить на вопрос, каким же образом задаются пользовательские функции.
Если мы попытаемся определить некоторую функцию, используя уже хорошо нам известную операцию присваивания (или отложенного присваивания), то потерпим фиаско. Проиллюстрируем это на рис. 9.15. В примере In[1] мы пытаемся определить функцию возведения в квадрат синуса угла, присваивая выражению SinSquare[x] значение (Sin[x])2. В примере In[2] мы пытаемся применить нашу функцию SinSquare к числу Pi, выражениям y и x. Как мы видим в Out[2], вычисление произошло только для аргумента x. Дело в том, что, хотя пользователь рассматривает x как переменную, которая может принимать любые значения из области определения функции, Mathematica расценивает x как фиксированный символ, неизменное выражение. Поэтому выражение SinSquare[x] следует рассматривать как единое целое, а не как выражение, состоящее из двух функционально обособленных элементов SinSquare и [x]. Точно так же едиными и отличными от SinSquare[x] выражениями являются SinSquare[Pi] и SinSquare[y]. Поэтому SinSquare[x] везде будет заменяться выражением Sin[x]2, а два других будут оставаться неизменными.
Таким образом, наша задача сделать так, чтобы указываемый в квадратных скобках аргумент x функции с заголовком SinSquare воспринимался как переменная. Для этого необходимо вместе с x употребить подчёркивание " _ ", внутренняя форма которого — Blank[].
Таким образом, общий вид пользовательской функции следующий:
funcname[arg1_,arg2_,...]:= body
Левая часть выражения содержит имя функции funcname, которое в обязательном порядке должно являться символом. За именем функции следуют квадратные скобки, содержащие один или несколько разделённых запятыми символьных выражений, каждое из которых оканчивается нижним подчёркиванием. Эти символы выступают в качестве имён аргументов функции.
В правой части выражения содержится непосредственно определение функции, которое называется телом функции: оно может состоять из одного единственного выражения — так называемый "однострочник" (one-liner), или включать целый ряд выражений — составная функция (compound function). Имена аргументов, заданных в левой части, используются в правой части без нижнего подчёркивания.
Пользовательские функции принято определять при помощи отложенного присваивания " := ". При этом выражение, которым задаётся пользовательская функция, ничего не генерирует, и не образуется ячейки Out; в момент задания тело функции не вычисляется. Вычисление происходит лишь в момент повторного обращения к функции.
В примере In[1] на рис. 9.16 мы, наконец, задаём функцию возведения в квадрат синуса некоторого выражения. В In[2] на рис. 9.16 мы проводим проверку действия нашей функции на разные выражения (аналогично примеру In[2] на рис. 9.15) и по полученному результату Out[2] убеждаемся в её работоспособности.
Подробней о задании пользовательских функций см. книги Е. М. Воробьёва [1, с. 126–129] и П. Веллина и др. [14, с. 88–89].
9.3.2 Чистые и анонимные функции
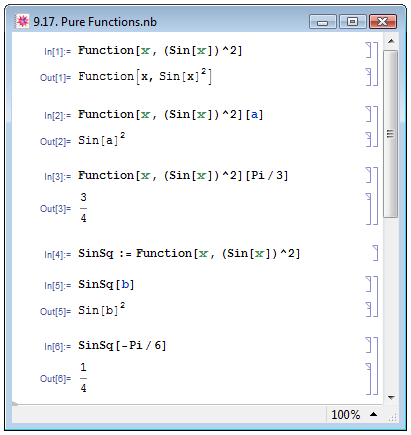
В предыдущем пункте мы научились самостоятельно определять функции: при этом все заданные таким образом функции в обязательном порядке являются именованными, то есть, имеют заголовки. Однако заголовки имеет смысл определять, если эти функции будут использоваться в дальнейшем тексте программы. Если же новая функция будет использована единожды или считанное число раз, "полезно работать с так называемыми чистыми функциями, которые используются только в момент их создания" (Е. М. Воробьёв [1, с. 129]). Для определения чистых функций служит выражение Function. В простейшей своей форме Function[x,body] задаёт функцию одной переменной x, причём в качестве переменной вместо x может использоваться любой символ: в использовании нижнего подчёркивания здесь необходимости нет. Выражение Function[{x1,x2,...},body] задаёт функцию нескольких переменных. Выражение body задаётся так же, как правая часть выражения, задающего пользовательскую функцию. В качестве примера In[1] на рис. 9.17 зададим чистую функцию возведения в квадрат синуса угла, аналогичную таковой в примере In[1] на рис. 9.16.
Выражение, к которому следует применить заданную чистую функцию, необходимо указать в квадратных скобках сразу после выражения Function[...] (примеры In[2] и In[3] на рис. 9.17). Чистую функцию очень просто превратить в именованную, присвоив её выражение некоторому символу (примеры In[4] – In[6] на рис. 9.17).
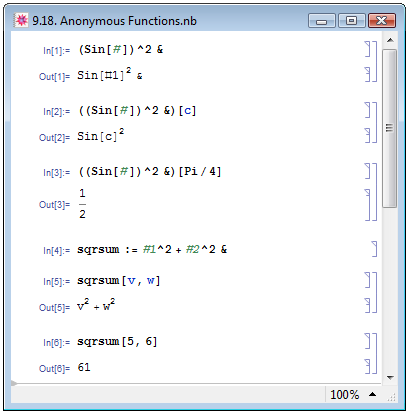
Е. М. Воробьёв [1, с. 130] пишет: "Существует более компактная и удобная форма представления чистой функции, которую иногда называют анонимной функцией. В анонимных функциях вместо связанных переменных используются специальные выражения "Математики" с заголовком Slot, имеющие вид #, #1 и т.д. При этом для функций одной переменной используется #, а в функциях нескольких переменных первый аргумент обозначается #1, второй #2 и т.д. Кроме того, в конце анонимной функции ставится знак &". В примере In[1] на рис. 9.15 мы снова определяем функцию вычисления квадрата синуса угла, но делаем это посредством задания анонимной функции. Чтобы применить заданную функцию к некоторому выражению, следует также указать его в квадратных скобках сразу после определения функции (примеры In[2] и In[3] на рис. 9.18).
На рис. 9.18 также приведён пример In[4] задания именованной анонимной функции двух переменных для вычисления суммы квадратов двух выражений, а также примеры In[5] и In[6] использования этой функции.
Использование анонимных функций оказывается наиболее эффективным в сочетании с другими функциями. В примере In[1] на рис. 9.19 зададим некоторый список list={1,7,3,5,6,4,3}. В примере In[2] при помощи функции Map выполним заданный набор действий (возведём во вторую степень и удвоим результат) с элементами списка list, причём набор действий определим при помощи анонимной функции.
Очень полезными оказываются анонимные функции при работе со списками. Предназначенная для сортировки элементов списка функция Sort, с которой мы познакомились в третьей лекции настоящего курса, может иметь необязательный аргумент, задающий условие сортировки: он должен быть двухместным предикатом, и сортировка производится так, чтобы он принимал значение True (Е. М. Воробьёв [1, с. 131]). Этот аргумент может быть задан в форме анонимной функции. В примере In[3] на рис. 9.19 мы осуществляем сортировку элементов списка list по убыванию их абсолютного значения, причём условие сортировки задаём как анонимную функцию. В примере In[4] на рис. 9.19 при помощи функции Select мы выбираем только элементы, принадлежащие отрезку от -4 до 4, причём условие выбора мы также задаём в виде анонимной функции.
Подробней о чистых и анонимных функциях см. книги Е. М. Воробьёва [1, с. 129–131] и П. Веллина и др. [14, с. 102–105].