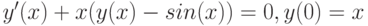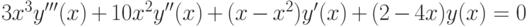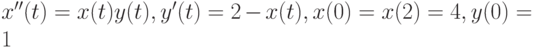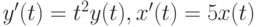Уравнения. Системы уравнений
8.5. Нахождение решений рекуррентных уравнений
Рекуррентными называются функции, значение которых в одной точке зависит от значения этой же функции в другой точке. Отношения между значениями функции в разных точках задаются рекуррентными уравнениями. Решает рекуррентные уравнения функция RSolve: в качестве результата она выдаёт зависимость значения функции от номера итерации. Задаётся функция в виде RSolve[eq,f[n],n], т.е. имеет, по крайней мере, три аргумента: первый — уравнение (систему уравнений) eq с начальными условиями, второй — функция (или список функций) f[n], которая зависит от номера итерации, счётчик которых n указываемой в третьем аргументе. Решение рекуррентного уравнения приведено в примерах In[1] и In[2] на рис. 8.21. Как мы видим, оба расчёта имеют одинаковый результат (ср. Out[1] и Out[2]) при том, что номера итераций указаны различным образом.
Функцию RSolve можно рассматривать как дискретный аналог DSolve. Именно поэтому специальные функции, генерируемые DSolve при решении дифференциальных уравнений, встречаются и при решении рекуррентных уравнений. В примере In[3] на рис. 8.21 при решении рекуррентного уравнения мы получили зависимость, содержащую функцию Бесселя.
О решении рекуррентных уравнений см. книгу В. П. Дьяконова [2, с. 263–264].
Ключевые термины
Рекуррентными называются функции, значение которых в одной точке зависит от значения этой же функции в другой точке.
Трансцендентное уравнение — уравнение, не являющееся алгебраическим.
Краткие итоги
В данной лекции мы познакомились с основными встроенными функциями Mathematica для нахождения символьных и численных решений алгебраических, трансцендентных, рекуррентных и дифференциальных уравнений, а также систем уравнений. Мы познакомились с принципами работы некоторых встроенных функций решения уравнений. Также мы научились сочетать возможности Mathematica символьных вычислений, численных расчётов и графических средств для нахождения решений уравнений и систем уравнений.
Вопросы
- Какая функция Mathematica используется для нахождения символьных решений алгебраических уравнений? В каком виде задаются её аргументы? В каком виде она возвращает результат вычислений?
- Каким образом Mathematica представляет корни полиномиального уравнения в случае, если она не может представить полученное при помощи функции Solve решение в аналитическом виде?
- Каким образом Mathematica может отреагировать на попытку решить при помощи функции Solve трансцендентное уравнение?
- Какое действие выполняет функция FindInstance, применённая к алгебраическому уравнению? В каком виде задаются её аргументы?
- Для каких целей служит функция Eliminate?
- В каких случаях при работе с алгебраическими уравнениями функции Solve следует предпочесть функцию Reduce? В каком виде возвращается результат выполнения функции Reduce?
- Для чего используется функция SolveAlways? Какие обязательные аргументы она содержат?
- В каком виде должны быть заданы аргументы функции решения систем линейных уравнений LinearSolve?
- Какая функция Mathematica используется для нахождения численных решений алгебраических уравнений? В каком виде она возвращает результат вычислений?
- В каких случаях при решении уравнений используется функция FindRoot? Каким образом она ищет корни уравнений? Для чего используется опция MaxIterations?
- Для решения каких типов ДУ и систем ДУ используется функция DSolve? Какие обязательные аргументы она содержат?
- В чём заключается разница в результатах вычислений при задании второго аргумента функции DSolve как f и f[x]?
- В чём состоят отличия при задании аргументов функций аналитического DSolve и численного NDSolve решения ДУ?
- В каком виде возвращает результат решения функция NDSolve?
- Для каких целей используется функция RSolve? В каком виде задаются её обязательные аргументы?
Упражнения
- Решите средствами Mathematica следующие уравнения и системы уравнений. Для каждого уравнения или системы уравнений используйте по два наиболее подходящих способа решения, если это возможно. Сравните результаты решения каждым из способов друг с другом.


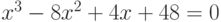
 (относительно
(относительно  )
) (относительно
(относительно  )
)

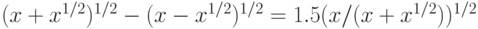
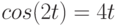
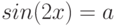 (относительно
(относительно  )
)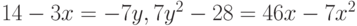

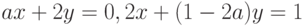 (относительно
(относительно  и
и  )
) ,
, 
 ,
, 
 (относительно
(относительно  и
и  )
)

- Из приведённых ниже систем уравнений исключите указанные переменные.
 ,
,  (исключить переменную
(исключить переменную  )
) ,
,  (переменную
(переменную  )
) ,
,  ,
,  (переменную
(переменную  )
) ,
,  ,
,  (переменные
(переменные  и
и  )
) ,
,  ,
,  (переменные
(переменные  ,
,  и
и  )
) (переменную
(переменную  )
) ,
,  (переменную
(переменную  )
) (переменные
(переменные  и
и  )
) (переменную
(переменную  )
) - Решите средствами Mathematica следующие ДУ и системы ДУ. Проиллюстрируйте полученные решения графически, если это возможно.