Уравнения. Системы уравнений
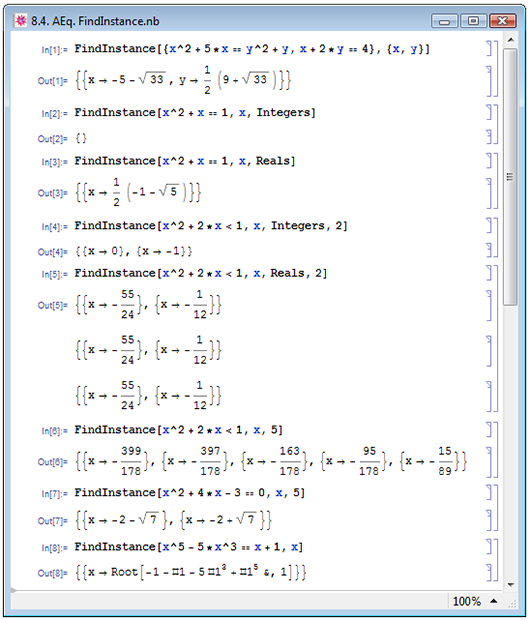
Ещё одна функция нахождения корней уравнения или системы уравнений является функция FindInstance. Заданная в простейшем виде FindInstance[syseqns,vars] функция находит один набор значений переменных vars, при которых уравнения системы syseqns становятся верными тождествами (пример In[1] на рис. 8.4). Помимо уравнений функция умеет находить и отдельные решения неравенств. В расширенном виде с дополнительным аргументом функция FindInstance[syseqns,vars,dom] выбирает только те выражения, которые принадлежат к типу данных dom. Выражение Integers задаёт целочисленные данные, Complexes — комплексные. А вот с выражением Reals всё не так однозначно. Если в исходном уравнении все численные коэффициенты заданы точно, то функция FindInstance с аргументом Reals всё равно будет стараться искать точные решения неравенства или корни уравнения: отличие от Integers состоит в том, что под этот критерий подпадают рациональные выражения и комбинации целочисленных и рациональных выражений — ср. результаты вычисления In[2] и In[3]. Приближённые результаты (в виде вещественных чисел) функция FindInstance вернёт, если хотя бы один коэффициент исходного уравнения или неравенства был задан приближённо.
Функция в виде FindInstance[syseqns,vars,dom,n] находит n или менее наборов значений vars, принадлежащих к типу данных dom (примеры In[4] и In[5] на рис. 8.4). Аргумент dom может быть опущен (пример In[6]).
Безусловно, FindInstance не может найти больше корней, чем их на самом деле имеет уравнение. Так количество корней полиномиальных уравнений не может превышать наибольшей степени переменной в этих уравнениях. В примере In[7] на рис. 8.4 мы пытаемся заставить Mathematica найти пять корней квадратного уравнения, хотя знаем, что их всего два. Только эти два корня сумела отыскать и Mathematica — см. Out[7].
Функция FindInstance также может представлять результат вычисления в виде Root-объектов (пример In[8] на рис. 8.4).
увеличить изображение
Рис. 8.4. Нахождение считанного числа корней уравнений, систем уравнений, решений неравенств и систем неравенств при помощи функции FindInstance
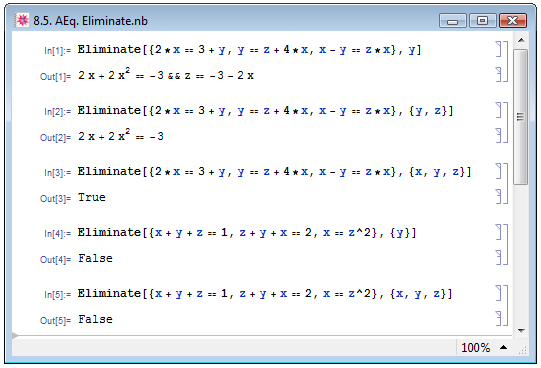
Один из методов решения систем алгебраических уравнений некомпьютерными методами, вручную, заключается в поэтапном представлении одной переменной через другие: при этом уменьшается и количество уравнений, и количество переменных. Для реализации подобной процедуры служит функция Eliminate. Задаётся она в единственной форме Eliminate[syseqns,vars] и исключает переменные vars из системы уравнений syseqns путём их выражения через оставшиеся переменные (примеры In[1] и In[2] на рис. 8.5). Результатом действия функции Eliminate может являться уравнение (см. Out[2]) или система уравнений (Out[1]) в зависимости от количества уравнений в первом аргументе syseqns и количества переменных во втором vars.
Если система уравнений syseqns имеет решение, то функция Eliminate[syseqns,vars] возвращает True, если в списке переменных vars, которые следует исключить, указать все переменные системы syseqns — пример In[3] на рис. 8.5. Если система не имеет решений вовсе, то независимо от количества переменных в аргументе vars функция Eliminate будет возвращать False — примеры In[4] и In[5].
Подробней о функции Eliminate см. книгу А. Н. Прокопени и А. В. Чичурина [5, с. 30].
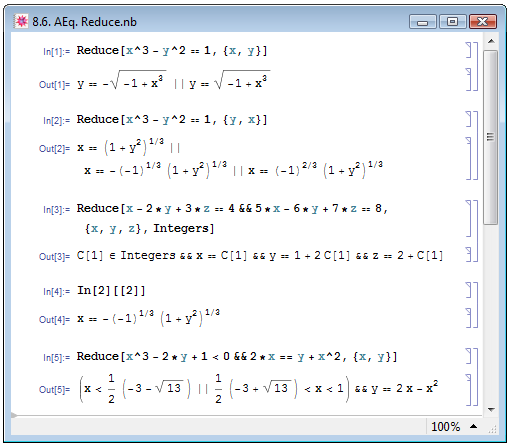
По поводу полученных при помощи функции Solve решений Е. М. Воробьёв [1, с. 49–50] пишет следующее: "Функция Solve находит решения уравнений, трактуя их "в общем положении", т.е. для неспецифических значений входящих в уравнения символьных параметров". Иллюстрацию этого утверждения мы находим в Out[1] на рис. 8.1: очевидно, что оба выражения для корней не имеют смысла при a=0. Выход из сложившейся ситуации предлагают А.Н. Прокопеня и А. В. Чичурин [5, с. 30]: "Если уравнение или система уравнений содержит параметры, причём решение существует не при любых значениях параметров, то для решения системы удобно использовать функцию Reduce. В этом случае результат получается в виде набора уравнений, который содержит все возможные решения, включая дополнительные условия на параметры". Заданная в простейшем виде функция Reduce[syseqns,vars] ищет решения в общем виде независимо от потенциальной принадлежности решений к тому или иному типу численных данных (примеры In[1] и In[2] на рис. 8.6). Добавление третьего аргумента dom производит тот же эффект, что и в случае функции FindInstance: Reduce[syseqns,vars,dom] выбирает только решения, принадлежащие к типу данных dom; выражение dom может принимать значении Integers, Reals и Complexes (пример In[3]).
Если в результате выполнения функции Reduce был получен набор из нескольких уравнений, то обратиться к конкретному уравнению оказывается возможным тем же методом, который используется при работе с функцией Solve — при помощи двойных скобок [[]]. В примере In[4] на рис. 8.6 мы обращаемся ко второму уравнению, полученному в результате вычисления In[2].
Кроме того, Reduce позволяет решать параметрически заданные неравенства, системы неравенств и системы неравенств и уравнений (пример In[5] на рис. 8.6).
Ещё одна функция для работы с параметрическими уравнениями — SolveAlways: она находит значение параметров, при которых уравнения системы удовлетворяются при любых значениях переменных. Задаётся она также с двумя обязательными аргументами: уравнением или системой уравнений и переменной или списком переменных — SolveAlways[syseqns,vars]. Примеры использования функции см. на рис. 8.7.
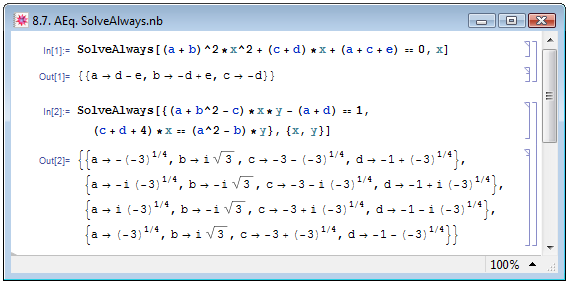
Рис. 8.7. Нахождение универсальных значений параметров для превращения уравнения в тождество при помощи функции SolveAlways
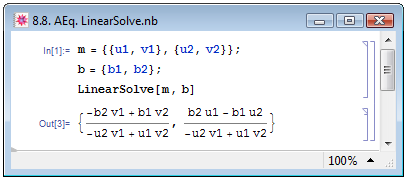
Во многих случаях на практике, если в процессе работы возникла необходимость решить систему линейных уравнений, часто оказывается, что задана не сама система, а матрица её коэффициентов. Если система уравнений задана в матричной форме m x=b, где m — квадратная матрица коэффициентов, а x и b — векторы переменных и свободных членов уравнений системы в правой части, соответственно, решить её можно при помощи функции LinearSolve[m,b] [5, с. 31] — примеры на рис. 8.8. Как пишет Е. М. Воробьёв [1, с. 51]: "Функция LinearSolve наиболее эффективна в случае систем большой размерности с разреженными матрицами коэффициентов".
Подробней о функциях SolveAlways и LinearSolve см. книги Е. М. Воробьёва [1, с. 50–51] и А. Н. Прокопени и А. В. Чичурина [5, с. 31].