|
поддерживаю выше заданые вопросы
|
Умножение разреженных матриц
Символическое и численное разложение
Вернемся теперь к исходной задаче решения системы уравнений
Ax=b,
Как уже было сказано, при решении задачи с разреженной матрицей A выделяют этапы переупорядочивания, символического разложения, численного разложения и обратного хода.
Методы переупорядочивания, т.е. вычисления матрицы перестановки P с целью минимизации заполнения фактора, были изложены в предыдущем пункте. Сейчас же мы коснемся вопросов, возникающих при символическом разложении, т.е. при построении портрета матрицы L.
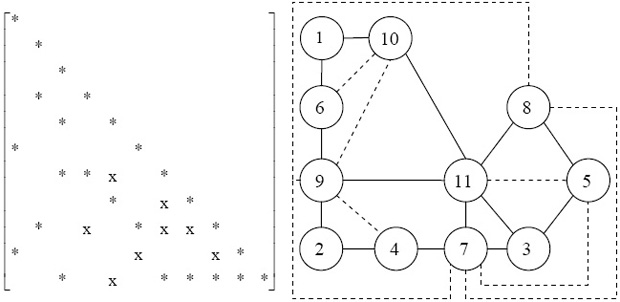
Алгоритмические трудности, возникающие при разложении разреженной симметричной матрицы, лучше всего разъяснить с помощью примера. При этом конкретные численные значения нас не будут интересовать; для простоты в матрице, внешний вид которой приведен на рис. 7.45, будут обозначены только позиции ненулевых элементов нижнего треугольника.
Разложение матрицы из примера начнется с четвертого столбца, поскольку в строках 1-3 все элементы слева от диагонали равны нулю. При этом в столбце 4 появляется новый ненулевой элемент, а именно элемент 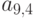 . На рис. новые ненулевые элементы отмечены символом x. Далее обрабатывается столбец 5; при этом возникнут новые ненулевые элементы
. На рис. новые ненулевые элементы отмечены символом x. Далее обрабатывается столбец 5; при этом возникнут новые ненулевые элементы 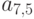 и
и 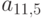 . Затем обрабатываем столбец 6, что приводит к появлению элемента
. Затем обрабатываем столбец 6, что приводит к появлению элемента  . Предполагая, что разложение доведено до этого места, мы подробно рассмотрим обработку столбца 7.
. Предполагая, что разложение доведено до этого места, мы подробно рассмотрим обработку столбца 7.
Запишем конкретный вид формул (7.13), (7.14) метода Холецкого, по которым будет вычисляться столбец 7. Элемент 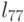 вычисляется по формуле
вычисляется по формуле
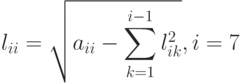
и будет всегда положительный (в силу положительной определенности матрицы A), а остальные элементы вычисляются как
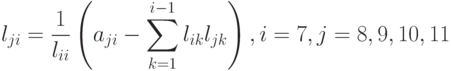 |
( 7.48) |
Равенство нулю указанных элементов будет определяться как начальной структурой самого столбца 7, так и структурой предшествующих столбцов. Отметим, что здесь мы не рассматриваем случай обнуления элементов в результате операции вычитания. Если такой случай и произойдет, то будем хранить нуль как элемент матрицы в явном виде.
Следуя формуле вычисления элементов столбца, можно сделать вывод, что портрет столбца 7 при разложении получается как объединение портретов столбцов 1-6 с ненулевыми элементами в 7-й строке в факторе L и портрета исходного столбца 7.
Для удобства последующего изложения будем использовать обозначение 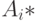 для i-й строки матрицы A, и
для i-й строки матрицы A, и 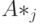 – для j-го столбца. Введем также обозначения для портретов i-й строки и j-го столбца матрицы соответственно
– для j-го столбца. Введем также обозначения для портретов i-й строки и j-го столбца матрицы соответственно
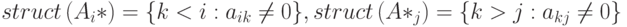
Предположим теперь, что все шаги, необходимые для определения портретов нужных столбцов проведены, и мы имеем следующие списки строчных индексов для ненулевых элементов, находящихся в строке 7 слева от диагонали:

Чтобы получить портрет нового столбца 7, эти списки индексов нужно слить. Для этого можно использовать эффективный метод переменного переключателя [10]. Результатом будет неупорядоченное представление нового столбца 7: 7, 11, 9, 8.
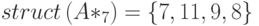
В общем случае для определения портрета некоторого j-го столбца приходится выполнить слияние, вообще говоря, j списков, что является трудоемкой операцией.
Замечательный факт, позволяющий существенным образом сократить трудоемкость вычисления портрета j-го столбца, состоит в том [9], что надо объединять не все портреты предшествующих столбцов с номерами 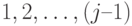 , а только те из них, в которых ненулевой элемент в j-й строке является первым ненулевым элементом данного столбца ниже диагонали.
, а только те из них, в которых ненулевой элемент в j-й строке является первым ненулевым элементом данного столбца ниже диагонали.
В рассмотренном примере для вычисления портрета столбца 7 нужно объединить лишь портреты столбцов 4, 5 и 7, при этом портрет столбца 5 уже будет содержать в себе все ненулевые элементы столбца 3:
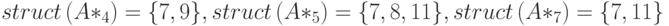
При их слиянии получаем портрет столбца 7
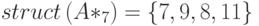
Заметим, символический этап разложения не требует, чтобы представления столбцов были упорядоченными. В самом деле, мы должны лишь регистрировать, у каких столбцов первый ненулевой элемент под диагональю находится в данной строке. Это означает, что остальные ненулевые элементы таких столбцов расположены ниже рассматриваемой строки, и чтобы сформировать портрет нового столбца нам нужны все эти элементы, каков бы ни был их порядок.
Таким образом, символический этап разложения исключения не требует упорядоченности представления. Это выгодно для нас, поскольку, как видно из примера, символический алгоритм порождает неупорядоченные портреты.
Для регистрации столбцов, имеющих первый ненулевой элемент в данной строке, мы должны сопоставить каждой строке свое множество столбцов. Например, столбцы 4 и 5 принадлежат множеству, ассоциированному со строкой 7. При практической реализации наименьший строчный индекс каждого столбца определяется одновременно с формированием его портрета, после чего к множеству добавляется номер данного столбца. Например, при сборке портрета столбца 7 выясняется, что ниже диагонали наименьший строчный индекс равен 8, и во множество, ассоциированное со строкой 8, вставляется номер 7. При обработке столбца 8 в соответствующем множестве будет обнаружен индекс 7 и будет использован портрет столбца 7.
Рассмотрим теперь этап численного разложения. Предположим, что символическое разложение и упорядочение портрета уже проделаны. Отметим, что упорядочить представление можно, дважды применив к матрице алгоритм символического транспонирования [10].
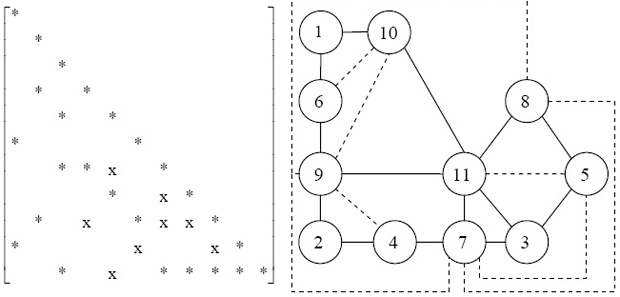
Вернемся опять к рассмотрению примера, изображенного на рис. 7.45. Предположим, что численное разложение выполнено вплоть до столбца 6, и исследуем процесс обработки столбца 7. Мы знаем, что ненулевые элементы столбца 7 расположены в строках 7, 8, 9 и 11. Чтобы вычислить их значения, нужно просмотреть строку 7, установить, что столбцы 3, 4 и 5 имеют ненулевые элементы в этой строке, найти в этих столбцах ненулевые элементы, строчные индексы которых не меньше 7, наконец, провести умножение и вычитание в соответствии с формулой (7.48). Рассмотрим одну из этих операций подробно (выполнение остальных операций основано на схожих идеях).
Предполагаем, что матрица хранится в разреженном столбцовом формате. Пусть нужно найти элементы данного столбца (например, столбца 3), у которого строчные индексы больше или равны номеру обрабатываемого столбца (например, столбца 7). Для описания столбца 3 в массивах values и rows начальной и конечной позициями являются pointer[3] и pointer[4]-1. Столбец 3 упорядочен:
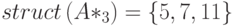
Однако нам нужна только та часть столбца 3, которая начинается со строки 7. Поэтому требуется другой указатель начала (например, pointerP[3]); в то же время pointer[4]-1 попрежнему можно использовать как указатель конца. В момент обработки столбца 7 pointerP[3] указывает позицию ненулевого элемента столбца 3, стоящего в строке 7. После того как столбец 3 использован для обработки столбца 7, значение pointerP[3] увеличивается на единицу. Так как столбец 3 упорядочен, pointerP[3] будет теперь указывать позицию следующего ненулевого элемента столбца 3, т. е. элемента из строки 11; это значение сохранится до обработки столбца 11. Дело в том, что при обработке столбцов 8, 9, 10 столбец 3 не будет использован, поскольку не имеет ненулевых элементов в строках 8, 9 и 10, а значит и значение pointerP[3] не будет изменено.
Подробное рассмотрение последовательных алгоритмов символического и численного разложения может быть найдено в книге [10].
Организация параллельных вычислений
Сейчас давайте обсудим, какие дополнительные возможности для распараллеливания возникают в случае разложения разреженных матриц по сравнению с плотными. Для этого нам опять потребуются некоторые сведения из теории графов.
В п. 7.5.3.1 было введено понятие графа G(A), соответствующего матрице A. Рассмотрим также граф заполнения F(A), который определяется как G(A) с дополнительными ребрами, соединяющими вершины i и j, для которых 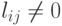 . Иными словами,
. Иными словами, 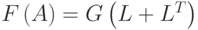 , т.е. это граф с матрицей смежности, образованной из фактора Холецкого L.
, т.е. это граф с матрицей смежности, образованной из фактора Холецкого L.
Используя введенное ранее обозначение для портрета столбца, определим на графе заполнения функцию parent следующим образом:
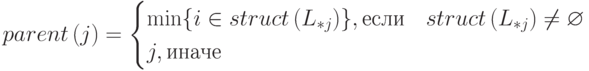
Введенная нами функция определяет строчный индекс первого ненулевого внедиагонального элемента в столбце j матрицы L.
Определим теперь дерево исключения T(A) как граф с n вершинами с дугами между вершинами i и j 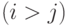 , где
, где  .
.
Дерево исключения T(A) является остовным деревом графа заполнения F(A) с корнем в nй вершине.
Отметим, что на этапе символического разложения фактически происходит построение дерева исключения T(A), специальная процедура для его построения не требуется.
Важность дерева исключения состоит в том, что оно определяет зависимость по данным между столбцами матрицы L при численном разложении. Значения столбца с номером, соответствующим некоторой вершине дерева, зависят от всех столбцов, номера которых содержатся в поддереве с корнем в данной вершине. При этом если 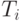 и
и 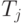 – непересекающиеся поддеревья дерева исключения T(A), то значения элементов столбцов с номерами, соответствующими вершинам поддерева
– непересекающиеся поддеревья дерева исключения T(A), то значения элементов столбцов с номерами, соответствующими вершинам поддерева 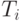 , не зависят от значений столбцов с номерами, соответствующими вершинам поддерева
, не зависят от значений столбцов с номерами, соответствующими вершинам поддерева 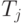 . Указанное свойство дает возможность вычислить значения таких столбцов параллельно.
. Указанное свойство дает возможность вычислить значения таких столбцов параллельно.
Например, в соответствии с деревом исключения, представленном на рис. 7.47, можно параллельно вычислить столбцы 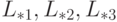 , затем – столбцы
, затем – столбцы 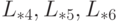 , и т.д.
, и т.д.
Более того, дерево исключения определяет зависимость по данным и при проведении обратного хода. Для непересекающиеся поддеревьев 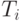 и
и 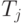 дерева исключения T(A) значения неизвестных с номерами, соответствующими вершинам поддерева
дерева исключения T(A) значения неизвестных с номерами, соответствующими вершинам поддерева 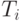 , не зависят от значений неизвестных с номерами, соответствующими вершинам поддерева
, не зависят от значений неизвестных с номерами, соответствующими вершинам поддерева 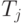 , что позволяет выполнить обратный ход параллельно.
, что позволяет выполнить обратный ход параллельно.
Конечно, при однократном решении СЛАУ распараллеливание обратного хода не дает ощутимого эффекта в силу его малой (по сравнению с прямым ходом) трудоемкости. Однако при решении серии СЛАУ с одинаковой матрицей и разными правыми частями ускорение может быть существенным.
Дерево исключения характеризует параллельный алгоритм разложения в целом, при этом высота дерева исключения является оценкой времени работы алгоритма (чем выше дерево, тем больше времени будет работать алгоритм), а ширина – оценкой степени параллелизма в задаче (чем шире дерево – тем больше степень параллелизма). Поэтому можно сказать, что для хорошего распараллеливания нужно иметь широкое, сбалансированное, относительно невысокое дерево исключения.
Для построения переупорядоченной матрицы A, обладающей деревом исключения T(A) с указанными свойствами, наиболее подходит метод вложенных сечений. В самом деле, на каждом шаге метода выбирается разделитель S, который соответствует одной (или нескольким последовательно связанным) вершинам дерева исключения 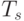 , а подмножества, которые получились в результате разделения графа, соответствуют поддеревьям с корнем в
, а подмножества, которые получились в результате разделения графа, соответствуют поддеревьям с корнем в 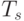 . Указанные поддеревья будут содержать примерно одинаковое количество узлов, что обеспечит хорошую сбалансированность дерева исключения.
. Указанные поддеревья будут содержать примерно одинаковое количество узлов, что обеспечит хорошую сбалансированность дерева исключения.
Рассмотренный нами метод минимальной степени тоже можно применять для переупорядочивания матрицы A в параллельном алгоритме, однако при этом не будет гарантии хороших свойств дерева исключения. Это подтверждают приведенные ниже результаты экспериментов.
Результаты экспериментов
Для иллюстрации мы опять вернемся к разложению матриц из п.3.5.3.2, и рассмотрим методы переупорядочивания с точки зрения их применимости в параллельном алгоритме.
Одним из свойств, характеризующих применимость перестановки для параллельного алгоритма, является высота дерева исключения. В табл. 3.14 приведены высоты деревьев исключения, получающихся после работы методов минимальной степени (Minimum Degree) и вложенных сечений (Nested Dissection) для рассматриваемых нами матриц.
| ND | MD | |
|---|---|---|
| shallow_water2 | 930 | 1459 |
| Pwtk | 5823 | 8062 |
| parabolic_fem | 2826 | 4891 |
| cfd2 | 6802 | 10723 |
Результаты, приведенные в таблице, подтверждают, что переупорядочивание по методу вложенных сечений дает дерево исключения с меньшей высотой, чем с использованием метода минимальной степени. Поэтому в дальнейших экспериментах мы будем использовать перестановку, полученную методом вложенных сечений.
Теперь рассмотрим время работы последовательного алгоритма при проведении символического разложения (обозначим это время как  ), численного разложения (
), численного разложения ( ) и обратного хода (
) и обратного хода (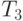 ).
).
 |
 |
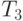 |
|
|---|---|---|---|
| shallow_water2 | 0,12 | 0,37 | 0,01 |
| Pwtk | 4,96 | 53,87 | 0,26 |
| parabolic_fem | 1,62 | 7,78 | 0,12 |
| cfd2 | 4,78 | 91,04 | 0,23 |
Очевидно, что основные временные затраты приходятся на этап численного разложения, поэтому именно данный этап нуждается в распараллеливании. Также можно распараллеливать и обратный ход, т.к. во многих задачах требуется решать серию систем с одинаковым портретом, но разными значениями матрицы, что требует однократного проведения символьного разложения и многократного проведения численного разложения и обратного хода.
Распараллеливание численного разложения и обратного хода будем проводить, выделяя непересекающиеся поддеревья в дереве исключения и параллельно обрабатывая соответствующие столбцы матрицы. С целью определения оптимальной высоты выделяемых поддеревьев проведем серию экспериментов на матрице parabolic_fem, в которой будем варьировать высота в диапазоне от 50 до 100 (напомним, что общая высота дерева исключения – 2826); результаты экспериментов приведены ниже.
| Высота поддерева | 1 поток | Параллельное численное разложение | |||||||
|---|---|---|---|---|---|---|---|---|---|
| 2 потока | 4 потока | 6 потоков | 8 потоков | ||||||
| t | S | t | S | t | S | t | S | ||
| 50 | 8,36 | 5,37 | 1,56 | 5,32 | 1,57 | 4,13 | 2,02 | 5,46 | 1,53 |
| 75 | 8,47 | 5,90 | 1,44 | 4,51 | 1,88 | 4,66 | 1,82 | 4,24 | 2,00 |
| 100 | 8,36 | 5,35 | 1,56 | 4,40 | 1,90 | 4,60 | 1,82 | 4,65 | 1,80 |
| Высота поддерева | 1 поток | Параллельный обратный ход | |||||||
|---|---|---|---|---|---|---|---|---|---|
| 2 потока | 4 потока | 6 потоков | 8 потоков | ||||||
| t | S | t | S | t | S | t | S | ||
| 50 | 0,15 | 0,08 | 1,82 | 0,07 | 2,30 | 0,06 | 2,63 | 0,05 | 2,87 |
| 60 | 0,15 | 0,09 | 1,69 | 0,06 | 2,49 | 0,06 | 2,39 | 0,06 | 2,57 |
| 100 | 0,17 | 0,09 | 1,85 | 0,06 | 2,68 | 0,06 | 2,74 | 0,05 | 3,06 |
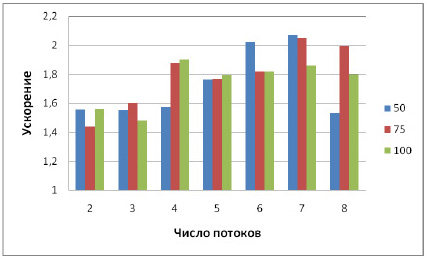
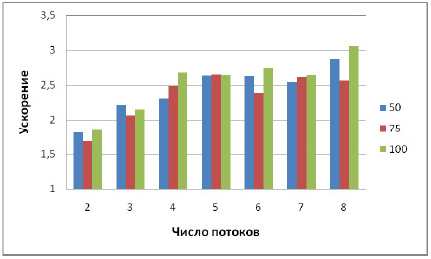
Эксперименты, проведенные на матрице parabolic_fem, показывают, что наибольшее ускорение обратного хода достигается при использовании поддеревьев высоты 100, а при численном разложении поддеревья высоты 75 и 100 дают примерно одинаковое ускорение, поэтому дальнейшие эксперименты будем проводить при использовании высоты 100.
| Матрица | 1 поток | Параллельное численное разложение | |||||||
|---|---|---|---|---|---|---|---|---|---|
| 2 потока | 4 потока | 6 потоков | 8 потоков | ||||||
| t | S | t | S | t | S | t | S | ||
| shallow_water2 | 0,34 | 0,23 | 1,47 | 0,22 | 1,57 | 0,20 | 1,69 | 0,22 | 1,57 |
| pwtk | 61,42 | 36,94 | 1,66 | 32,76 | 1,87 | 32,26 | 1,90 | 31,54 | 1,95 |
| parabolic_fem | 8,36 | 5,35 | 1,56 | 4,40 | 1,90 | 4,60 | 1,82 | 4,65 | 1,80 |
| cfd2 | 86,052 | 74,9 | 1,15 | 67,4 | 1,28 | 68,8 | 1,25 | 62,6 | 1,38 |
| Матрица | 1 поток | Параллельный обратный ход | |||||||
|---|---|---|---|---|---|---|---|---|---|
| 2 потока | 4 потока | 6 потоков | 8 потоков | ||||||
| t | S | t | S | t | S | t | S | ||
| shallow_water2 | 0,01 | 0,01 | 1,67 | 0,01 | 2,21 | 0,01 | 2,16 | 0,01 | 2,30 |
| pwtk | 0,25 | 0,15 | 1,63 | 0,13 | 1,93 | 0,13 | 1,98 | 0,12 | 2,06 |
| parabolic_fem | 0,17 | 0,09 | 1,85 | 0,06 | 2,68 | 0,06 | 2,74 | 0,05 | 3,06 |
| cfd2 | 0,28 | 0,2 | 1,64 | 0,1 | 2,26 | 0,2 | 1,79 | 0,2 | 1,50 |
Низкие показатели ускорения в данных задачах (максимальный – 3 при проведении обратного хода и 1,9 при численном разложении на 8 потоках) можно объяснить разбалансированностью дерева исключения. В задачах со сбалансированным деревом исключения можно ожидать больших показателей ускорения.