|
поддерживаю выше заданые вопросы
|
Умножение разреженных матриц
Методы решения систем с разреженной матрицей
В данном разделе будут рассмотрены вопросы, касающиеся решения СЛАУ с разреженными матрицами. В предыдущих разделах неявно подразумевалось, что мы работаем с плотными матрицами.
Понятие разреженной матрицы можно определить многими способами, суть которых состоит в том, что в разреженной матрице "много" нулевых элементов. Обычно говорят, что матрица разрежена, если она содержит 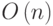 отличных от нуля элементов. В противном случае матрица считается плотной. Типичным случаем разреженности является ограниченность числа ненулевых элементов в одной строке от 1 до k, где
отличных от нуля элементов. В противном случае матрица считается плотной. Типичным случаем разреженности является ограниченность числа ненулевых элементов в одной строке от 1 до k, где  . Задачи линейной алгебры с разреженными матрицами возникают во многих областях, например, при решении дифференциальных уравнений в частных производных, при решении многомерных задач локальной оптимизации. В п. 7.3 мы уже познакомились с методами решения СЛАУ с трехдиагональной матрицей, которая, являясь ленточной, относится также и к классу разреженных матриц.
. Задачи линейной алгебры с разреженными матрицами возникают во многих областях, например, при решении дифференциальных уравнений в частных производных, при решении многомерных задач локальной оптимизации. В п. 7.3 мы уже познакомились с методами решения СЛАУ с трехдиагональной матрицей, которая, являясь ленточной, относится также и к классу разреженных матриц.
Очевидно, что любую разреженную матрицу можно обрабатывать как плотную, и наоборот. При правильной реализации алгоритмов в обоих случаях будут получены правильные результаты, однако вычислительные затраты будут существенно отличаться. Поэтому приписывание матрице свойства разреженности эквивалентно утверждению о существовании алгоритма, использующего ее разреженность и делающего операции с ней эффективнее по сравнению со стандартными алгоритмами.
Многие алгоритмы, тривиальные для случая плотных матриц, в разреженном случае требуют более тщательного подхода. Во многих алгоритмах обработки разреженных матриц можно выделить два этапа: символический и численный. На символическом этапе формируется портрет результирующей матрицы (т.е. определяются места ненулевых элементов в структуре матрицы); на численном этапе определяются значения ненулевых элементов результирующей матрицы. В качестве примера типовых операций с разреженными матрицами в данной главе будет рассмотрен алгоритм умножения разреженной матрицы на плотный вектор, а также круг вопросов, возникающих при использовании метода Холецкого для решения систем линейных уравнений с разреженной матрицей.
Хранение разреженной матрицы
Существуют различные форматы хранения разреженных матриц. Одни предназначены для хранения матриц специального вида (например, ленточных), другие обеспечивают работу с матрицами общего вида. Ниже рассмотрим некоторые весьма распространенные способы представления разреженных матриц, информацию о других способах можно найти, например, в [10].
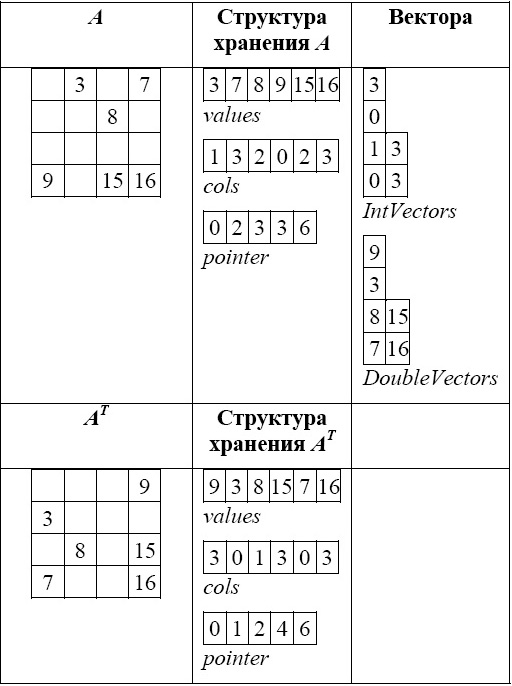
Повидимому, наиболее очевидным способом хранения произвольной разреженной матрицы является координатный формат: хранятся только ненулевые элементы матрицы, и их координаты (номера строк и столбцов). При данном подходе хранение матрицы A можно обеспечить в трех одномерных массивах:
- массив ненулевых элементов матрицы A (обозначим его как values);
- массив номеров строк матрицы A, соответствующих элементам массива values (обозначим его как rows);
- массив номеров столбцов матрицы A, соответствующих элементам массива values (обозначим его как cols);
Данный способ представления называют полным, поскольку представлена вся матрица А, и неупорядоченным, поскольку элементы матрицы могут храниться в произвольном порядке.
В качестве примера рассмотрим разреженную матрицу
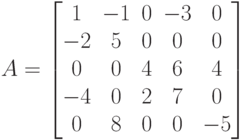 |
( 7.40) |
которая может быть представлена в координатном формате как
values=(1, -1, -3, -2, 5, 4, 6, 4, -4, 2, 7, 8, -5);
rows=(1, 1, 1, 2, 2, 3, 3, 3, 4, 4, 4, 5, 5);
cols=(1, 2, 4, 1, 2, 3, 4, 5, 1, 3, 4, 2, 5).
Хотя многие математические библиотеки поддерживают матрично-векторные операции в координатном формате, данный формат обеспечивает медленный доступ к элементам матрицы, и является затратным по используемой памяти. В рассмотренном выше примере избыточность по памяти образом проявляется в массиве rows, в котором строчные координаты хранятся неоптимальным образом.
Перейдем далее к рассмотрению более экономных форматов хранения. Разреженный строчный формат - это одна из наиболее широко используемых схем хранения разреженных матриц. Эта схема предъявляет минимальные требования к памяти и в то же время оказывается очень удобной для нескольких важных операций над разреженными матрицами: сложения, умножения, перестановок строк и столбцов, транспонирования, решения линейных систем с разреженными матрицами коэффициентов как прямыми, так и итерационными методами и т. д.
В соответствии с рассматриваемой схемой для хранения матрицы A требуется три одномерных массива:
- массив ненулевых элементов матрицы A, в котором они перечислены по строкам от первой до последней (обозначим его опять как values);
- массив номеров столбцов для соответствующих элементов массива values (обозначим его как cols);
- массив указателей позиций, с которых начинается описание очередной строки (обозначим его pointer). Описание k-й строки хранится в позициях с pointer[k]-й по (pointer[k+1]–1)-ю массивов values и cols. Если pointer[k]=pointer[k+1], то k-я строка пустая. Если матрица A состоит из n строк, то длина массива pointer будет n+1.
Данный способ представления также является полным, и упорядоченным, поскольку элементы каждой строки хранятся в соответствии с возрастанием столбцовых индексов.
Для примера рассмотрим представление матрицы (7.40) в разреженном строчном формате:
values=(1, -1, -3, -2, 5, 4, 6, 4, -4, 2, 7, 8, -5);
cols=(1, 2, 4, 1, 2, 3, 4, 5, 1, 3, 4, 2, 5);
pointer=(1, 4, 6, 9, 12, 14).
Очевидно, что объем памяти, требуемый для хранения вектора pointer, значительно меньше, чем для хранения вектора rows. Более того, разреженный строчный формат обеспечивает эффективный доступ к строчкам матрицы; доступ к столбцам по прежнему затруднен. Поэтому предпочтительно использовать этот способ хранения в тех алгоритмах, в которых преобладают строчные операции.
Иногда бывает удобно использовано полный неупорядоченный способ хранения, при котором внутри каждой строки элементы могут храниться в произвольном порядке. Результаты многих матричных операций получаются неупорядоченными, и упорядочивание может быть весьма затратным. В то же время, многие алгоритмы для разреженных матриц не требуют, чтобы представление было упорядоченным.
После рассмотрения строчного формата хранения очевидным является и разреженный столбцовый формат. В этом случае ненулевые элементы матрицы A перечисляются в порядке их появления в столбцах матрицы, а не в строках. Все ненулевые элементы хранятся по столбцам в массиве values; индексы строк ненулевых элементов – в массиве rows; элементы массива pointer указывают на позиции, с которых начинается описание очередного столбца.
Столбцовые представления могут рассматриваться как строчные представления транспонированных матриц. Разреженный столбцовый формат обеспечивает эффективный доступ к столбцам матрицы; доступ к строкам затруднен. Поэтому предпочтительно использовать этот способ хранения в тех алгоритмах, в которых преобладают столбцовые операции.
В случае если обрабатываемая матрица симметрична, достаточно хранить лишь ее верхнюю треугольную подматрицу. При этом для хранения можно использовать любой из рассмотренных форматов. Например, симметричная матрица
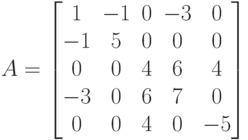
может быть представлена в разреженном строчном формате как
values=(1, -1, -3, 5, 4, 6, 4, 7, -5);
cols=(1, 2, 4, 2, 3, 4, 5, 4, 5);
pointer=(1, 4, 5, 8, 9, 10).
Если большинство диагональных элементов заданной симметричной матрицы отличны от нуля (например, у симметричной положительно определенной матрицы все диагональные элементы положительны), то они могут храниться в отдельном массиве BD, а разреженным форматом представляется только верхний треугольник В.
Завершая обзор форматов хранения разреженных матриц, можно еще раз отметить, что выбор способа хранения матрицы полностью определяется алгоритмами, которые планируется в дальнейшем использовать для обработки данной матрицы.
Базовые алгоритмы обработки разреженных матриц
Реализация матричных операций является тривиальной в случае плотной или ленточной матрицы, но не столь очевидна для разреженных матриц, хранящихся в одном из экономичных форматов (здесь и далее мы будем рассматривать разреженный строчный формат хранения матрицы).
Умножение матрицы на вектор
Рассмотрим операцию умножения разреженной матрицы на плотный вектор. Результатом этой операции будет заполненный вектор, а не разреженная матрица. Поэтому в алгоритмах умножения вычисления выполняются прямо, без символического этапа.
Среди алгоритмов, в которых встречается данная операция, можно отметить итерационные методы решения систем линейных уравнений. Достоинство данных методов, с вычислительной точки зрения, состоит в том, что единственная требуемая матричная операция, это повторное умножение матрицы на последовательность заполненных векторов; сама матрица не меняется.
Итак, рассмотрим умножение разреженной матрицы общего вида, хранимой в строчном формате посредством массивов values, cols, pointer на заполненный векторстолбец b, хранимый в одномерном массиве. Результатом будет новый заполненный вектор
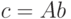
также размещаемый в одномерном массиве.
Пусть n – число строк матрицы. Порядок, в котором накапливаются скалярные произведения, определяется порядком хранения элементов матрицы. Для каждой ее строки i мы находим с помощью массива индексов pointer значения первой pointer[i] и последней pointer[i+1]–1 позиций, занимаемых элементами строки i в массивах values и cols. Затем, чтобы вычислить скалярное произведение строки i и вектора b, мы просто просматриваем values и cols на отрезке от pointer[i] до pointer[i+1]–1; каждое значение, хранимое в cols[pointer[j]], есть столбцовый индекс и используется для извлечения из массива b элемента, который должен быть умножен на соответствующее число из массива values. Результат каждого умножения прибавляется к c[i].
Рассмотрим теперь параллельный алгоритм умножения разреженной матрицы на плотный вектор, матрица представлена в строчном формате. При таком способе представления данных в качестве базовой подзадачи может быть выбрана операция скалярного умножения одной строки матрицы на вектор. После завершения вычислений каждая базовая подзадача определяет один из элементов вектора результата c.
Как правило, количество элементов в одной строке разреженной матрицы размера  ограничено некоторой константой k,
ограничено некоторой константой k,  . Значит, в процессе умножения такой матрицы на вектор количество вычислительных операций для получения скалярного произведения примерно одинаково для всех базовых подзадач. При использовании систем с общей памятью число потоков p будет меньше числа базовых подзадач n, и мы можем объединить базовые подзадачи таким образом, чтобы каждый поток выполнял несколько таких задач, соответствующих непрерывной последовательности строк матрицы А. В этом случае по окончании вычислений каждая базовая подзадача определяет набор элементов результирующего вектора с. Распределение подзадач между потоками может быть выполнено произвольным образом.
. Значит, в процессе умножения такой матрицы на вектор количество вычислительных операций для получения скалярного произведения примерно одинаково для всех базовых подзадач. При использовании систем с общей памятью число потоков p будет меньше числа базовых подзадач n, и мы можем объединить базовые подзадачи таким образом, чтобы каждый поток выполнял несколько таких задач, соответствующих непрерывной последовательности строк матрицы А. В этом случае по окончании вычислений каждая базовая подзадача определяет набор элементов результирующего вектора с. Распределение подзадач между потоками может быть выполнено произвольным образом.
Транспонирование матрицы
Рассмотрим задачу транспонирования разреженной матрицы A. Формально матрица 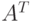 может быть определена как
может быть определена как
![A^T[i,j]=A^T[j,i]](/sites/default/files/tex_cache/20cad0cd683182f1b5bef1ae7c5f07dc.png)
и простейшая реализация данной операции в "плотном" случае оказывается эффективной. Однако в случае разреженной матрицы ситуация не столь очевидна, и простейшая реализация может существенно ухудшить показатели эффективности.
Будем формировать результирующую матрицу построчно. Для этого можно брать столбцы исходной матрицы и создавать из них строки результирующей матрицы. Но операция выделения из CRS-матрицы столбца №i является трудоемкой, т.к. данные в векторе values хранятся по строкам и для выборки данных по столбцу нужно просмотреть всю матрицу, что приводит к квадратичной (от числа ненулевых элементов) трудоемкости алгоритма. Необходимо другое решение. Подробно проблема транспонирования разреженной матрицы обсуждается в книге [10], здесь же рассмотрим основные идеи описанного в [10] алгоритма.
- Сформируем N одномерных векторов для хранения целых чисел (IntVectors), а также N векторов для хранения вещественных чисел (RealVectors). N в данном случае соответствует числу столбцов исходной матрицы.
- В цикле просмотрим все строки исходной матрицы, для каждой строки – все ее элементы. Пусть текущий элемент находится в строке i, столбце j, его значение равно v. Тогда добавим числа i и v в j-ые вектора для хранения целых и вещественных чисел (соответственно). Тем самым в векторах мы сформируем строки транспонированной матрицы.
- Последовательно скопируем данные из векторов в CRS структуру транспонированной матрицы (сols и values), попутно формируя массив pointer.
Рассмотрим пример (7.17).
При обходе исходной матрицы A формируются вектора IntVectors и RealVectors (число 3 расположено в строке 0 и столбце 1, следовательно, в IntVectors[1] добавляется 0, в RealVectors[1] добавляется 3 и т.д.). Далее вектора последовательно формируют структуру 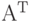 : обратите внимание на порядок следования элементов в массиве values матрицы
: обратите внимание на порядок следования элементов в массиве values матрицы 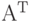 и его соответствие порядку элементов в массиве RealVectors (аналогично cols и IntVectors). Для формирования pointer достаточно подсчитать количество элементов в каждом из N векторов. pointer[0] всегда равно нулю, pointer[i]=pointer[i-1] + "Количество элементов в векторе i-1".
и его соответствие порядку элементов в массиве RealVectors (аналогично cols и IntVectors). Для формирования pointer достаточно подсчитать количество элементов в каждом из N векторов. pointer[0] всегда равно нулю, pointer[i]=pointer[i-1] + "Количество элементов в векторе i-1".
Таким образом, алгоритм транспонирует матрицу за линейное время, что значительно лучше исходного тривиального алгоритма. Недостатком же алгоритма в том виде, как он изложен, является использование дополнительной памяти. В книге [10] приводится описание алгоритма, лишенного этого недостатка. Основная идея состоит в использовании структур данных матрицы 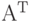 для промежуточных результатов вычислений.
для промежуточных результатов вычислений.
Матричное умножение
Приступим к обсуждению алгоритмов умножения разреженных матриц. Прежде всего рассмотрим алгоритм умножения непосредственно по определению.
Определение предполагает, что элемент в строке i и столбце j матрицы C вычисляется как скалярное произведение i-ой строки матрицы A и j-го столбца матрицы B. Какие особенности вносит разреженное представление?
Во-первых, используемая структура данных, построенная на основе формата CRS, предполагает хранение только ненулевых элементов, что усложняет программирование вычисления скалярного произведения, но одновременно уменьшает количество арифметических операций. При вычислении скалярных произведений нет необходимости умножать нули и накапливать полученный нуль в частичную сумму, что положительно влияет на сокращение времени счета. Пусть, например, в первом и втором векторах находится по 1% ненулевых элементов, при этом только десятая часть этих элементов расположена на соответствующих друг другу позициях. В этом случае расчет с использованием информации о структуре векторов может использовать в 1000 раз меньшее число умножений и сложений. Учитывая, что таких пар векторов 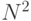 , получается существенное сокращение объема вычислений. К сожалению, не все так просто. Учет структуры векторов тоже требует машинного времени. Необходимо выполнить сопоставление номеров ненулевых
элементов с целью обнаружения пар значений, которые необходимо перемножить и накопить в частичную сумму.
, получается существенное сокращение объема вычислений. К сожалению, не все так просто. Учет структуры векторов тоже требует машинного времени. Необходимо выполнить сопоставление номеров ненулевых
элементов с целью обнаружения пар значений, которые необходимо перемножить и накопить в частичную сумму.
Во-вторых, необходимо научиться выделять вектора в матрицах A и B. В соответствии с определением, речь идет о строках матрицы A и столбцах матрицы B. Выделить строку матрицы в формате CRS не представляет труда: i-я строка может быть легко найдена, так как ссылки на первый элемент poiner[i] и последний элемент (pointer[i+1]-1) известны, что позволяет получить доступ к значениям элементов и номерам столбцов, хранящихся в массивах values и cols соответственно. Таким образом, проход по строке выполняется за время, пропорциональное числу ненулевых элементов в указанной строке, а проход по всем строкам – за время, пропорциональное NZ, где NZ – количество ненулевых элементов в матрице.
Проблема возникает с выделением столбца. Чтобы найти элементы столбца j необходимо просмотреть массив cols (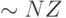 операций) и выделить все элементы, у которых в соответствующей ячейке массива cols записано число j. Если это нужно проделать для каждого столбца, необходимо
операций) и выделить все элементы, у которых в соответствующей ячейке массива cols записано число j. Если это нужно проделать для каждого столбца, необходимо 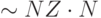 операций, что является неэффективным.
операций, что является неэффективным.
Возможное, но не единственное решение проблемы состоит в транспонировании матрицы B: после вычисления 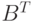 появится возможность эффективно работать со столбцами исходной матрицы B, а сам алгоритм транспонирования работает достаточно быстро. Другой вариант – для каждой CRSматрицы, которая может понадобиться в столбцовом представлении, дополнительно хранить транспонированный портрет. Сэкономив время на транспонировании, придется смириться с расходами времени на поддержание дополнительного портрета в актуальном состоянии. Есть и другие варианты решения проблемы, никак не связанные с транспонированием матрицы B (см., например, эффективный алгоритм Густавсона [11]). В дальнейшем мы будем использовать подход, основанный на транспонировании матрицы B.
появится возможность эффективно работать со столбцами исходной матрицы B, а сам алгоритм транспонирования работает достаточно быстро. Другой вариант – для каждой CRSматрицы, которая может понадобиться в столбцовом представлении, дополнительно хранить транспонированный портрет. Сэкономив время на транспонировании, придется смириться с расходами времени на поддержание дополнительного портрета в актуальном состоянии. Есть и другие варианты решения проблемы, никак не связанные с транспонированием матрицы B (см., например, эффективный алгоритм Густавсона [11]). В дальнейшем мы будем использовать подход, основанный на транспонировании матрицы B.
В-третьих, необходимо научиться записывать посчитанные элементы в матрицу C. Учитывая, что C хранится в формате CRS, важно избежать перепаковок. Для этого нужно обеспечить пополнение матрицы C ненулевыми элементами последовательно, по строкам – слева направо, сверху вниз. Это означает, что часто используемый в вычислениях на бумаге метод "возьмем первый столбец матрицы B, запишем его над матрицей A и перемножим на все строки…" не подходит. Нужно делать наоборот – брать первую строку матрицы A и умножать ее по очереди на все столбцы матрицы B (строки матрицы 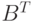 ). В этом случае обеспечивается последовательное пополнение матрицы С, позволяющее дописывать элементы в массивы values и cols, а также формировать массив pointer.
). В этом случае обеспечивается последовательное пополнение матрицы С, позволяющее дописывать элементы в массивы values и cols, а также формировать массив pointer.
Таким образом, для выполнения матричного умножения разреженных матриц необходимо сделать следующее:
- Реализовать транспонирование разреженной матрицы и применить его к матрице B.
- Инициализировать структуру данных для матрицы C, обеспечить возможность ее пополнения элементами.
- Последовательно перемножить каждую строку матрицы A на каждую из строк матрицы
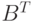 , записывая в C полученные результаты и формируя ее структуру.
, записывая в C полученные результаты и формируя ее структуру.
Еще один непростой момент: в процессе вычисления скалярного произведения на бумаге (в точной арифметике) может получиться нуль, причем не только в том случае, когда при сопоставлении векторов соответствующих друг другу пар не обнаружилось, но и просто как естественный результат. В арифметике с плавающей точкой нуль может получиться еще и в связи с ограничениями на представление чисел и погрешностью вычислений (см. стандарт IEEE-754). Нули, получившиеся в процессе вычислений, можно как хранить в матрице C (в векторе values в соответствующей позиции), так и не хранить; оба подхода имеют право на существование.
Как следует из приведенного описания, основной операцией является скалярное произведение двух разреженных векторов ( обозначим их 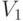 и
и 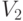 ), и к ее реализации нужно подойти с особой тщательностью.
), и к ее реализации нужно подойти с особой тщательностью.
Алгоритм подразумевает для каждой отличной от нуля компоненты вектора 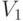 проверку, есть ли отличная от нуля компонента с таким же номером в векторе
проверку, есть ли отличная от нуля компонента с таким же номером в векторе 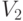 . Простейший вариант такой проверки имеет квадратичную трудоемкость, что существенно сказывается на эффективности.
. Простейший вариант такой проверки имеет квадратичную трудоемкость, что существенно сказывается на эффективности.
Заметим, что каждый умножаемый вектор является строкой матрицы и упорядочен в соответствии с выбранной структурой хранения матрицы. Это означает, что для сопоставления компонент может быть применен алгоритм, весьма похожий на слияние двух отсортированных массивов в один с сохранением упорядочивания. Алгоритм выглядит следующим образом:
- Встать на начало обоих векторов
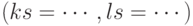
- Сравнить текущие элементы
![A.Col[ks] и B.Col[ls]](/sites/default/files/tex_cache/758ef3b6273a0b81f637bc0431160405.png) . Если значения совпадают, накопить в сумму произведение A.Value[ks] * B.Value[ls] и увеличить оба индекса, в противном случае – увеличить один из индексов, в зависимости от того, какое значение больше (например,
. Если значения совпадают, накопить в сумму произведение A.Value[ks] * B.Value[ls] и увеличить оба индекса, в противном случае – увеличить один из индексов, в зависимости от того, какое значение больше (например, ![A.Col[ks] > B.Col[ls] \rightarrow ls++](/sites/default/files/tex_cache/35b08e14ae58110190420725aabb80c3.png) ).
).
Шаг 2 выполняется до тех пор, пока не кончатся элементы хотя бы в одном из векторов.
Данный алгоритм имеет линейную трудоемкость, но он не очень хорошо соответствует архитектуре компьютера, т.к. содержит очень много ветвлений. Существуют более эффективные схемы: например, в книге [10] предлагается следующий алгоритм вычисления скалярного произведения разреженных векторов.
- Создадим дополнительный целочисленный массив X длины N. Инициализируем его числом -1. Обнулим вещественную переменную S.
- Просмотрим все ненулевые элементы первого вектора
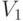 . Пусть такой элемент с порядковым номером i расположен в столбце с номером
. Пусть такой элемент с порядковым номером i расположен в столбце с номером ![j=V_1.cols[i]](/sites/default/files/tex_cache/75342b4484c2934f109da82d244bc95a.png) . В этом случае запишем i в j-ю ячейку массива X.
. В этом случае запишем i в j-ю ячейку массива X. - Просмотрим в цикле все ненулевые элементы второго вектора
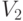 . Пусть элемент с порядковым номером k расположен в столбце с номером
. Пусть элемент с порядковым номером k расположен в столбце с номером ![z=V_2.cols[k]](/sites/default/files/tex_cache/ed652262823f4a12c56c2f68a0051caa.png) . Проверим значение
. Проверим значение ![X[z]](/sites/default/files/tex_cache/870d14dd412f5df9300f82817b8dd063.png) . Если оно равно -1, в первом векторе нет соответствующего элемента, т.е. умножение выполнять не нужно. Иначе умножаем
. Если оно равно -1, в первом векторе нет соответствующего элемента, т.е. умножение выполнять не нужно. Иначе умножаем ![V_2.values[k] и V_2.values[X[z]]](/sites/default/files/tex_cache/caf2a043d545ef937e4e9b7d00305b47.png) и накапливаем сумму в S.
и накапливаем сумму в S.
Данный алгоритм также имеет линейную (относительно числа ненулевых элементов в векторе) трудоемкость, и не содержит избыточных ветвлений.
В заключение отметим, что рассмотренные нами базовые алгоритмы демонстрируют типичные трудности, которые возникают при реализации очевидных "плотных" алгоритмов в "разреженном" случае.
Метод Холецкого для разреженных матриц
В п. 7.2 был рассмотрен метод Холецкого для решения системы линейных уравнений с симметричной положительно определенной матрицей
 |
( 7.41) |
при этом подразумевалось, что матрица A – плотная. Данный алгоритм, естественно, будет применим и для разреженной матрицы A, однако в этом случае возникает ряд важных моментов, к обсуждению которых мы сейчас и приступаем.
В качестве примера рассмотрим систему уравнений
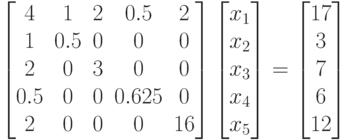 |
( 7.42) |
Используя расчетные формулы метода (7.13) и (7.14), можно вычислить фактор Холецкого для данной задачи
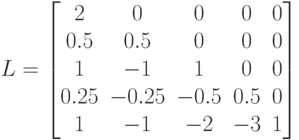
а затем, выполнив обратный ход алгоритма по формулам (7.15), (7.16), найти искомое решение
![x^T=[2, 2, 1, 8, 0.5]](/sites/default/files/tex_cache/432f99a0607a242b9712bf80ab66d40f.png)
Этот пример иллюстрирует наиболее важный факт, относящийся к применению метода Холецкого для разреженных матриц: матрица обычно претерпевает заполнение. Это значит, что в матрице L появляются ненулевые элементы в позициях, где в нижней треугольной части A стояли нули.
Предположим теперь, что мы перенумеровали переменные в соответствии с правилом 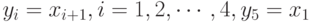 и переупорядочили уравнения так, чтобы первое стало последним, а остальные сдвинулись бы на единицу вверх. Тогда мы получим эквивалентную систему уравнений
и переупорядочили уравнения так, чтобы первое стало последним, а остальные сдвинулись бы на единицу вверх. Тогда мы получим эквивалентную систему уравнений
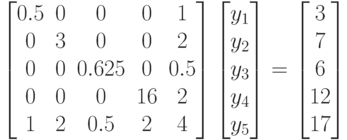 |
( 7.43) |
Очевидно, что эта перенумерация переменных и переупорядочение уравнений равносильны симметричной перестановке строк и столбцов матрицы A, причем та же перестановка применяется и к вектору b. Решение новой системы есть переупорядоченный вектор x. Указанную перенумерацию легко записать в виде произведения матицы A на матрицу перестановки P. Напомним, что матрица P называется матрицей перестановки, если в каждой строке и столбце матрицы находится лишь один единичный элемент. В нашем примере
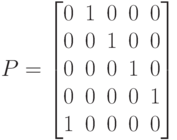 |
( 7.44) |
а матрицу системы (7.43) можно получить как
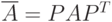
При этом связь с исходной постановкой задачи выражается соотношением
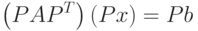
Ниже приведен фактор Холецкого для новой системы уравнений (с точностью до 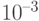 )
)

Выполнив обратный ход, можно получить переупорядоченный вектор решения
![y^T=[2, 1, 8, 0.5, 2]](/sites/default/files/tex_cache/a9123776f7107cee1ec5786666e82b39.png)
Важный момент состоит в том, что переупорядочение уравнений и переменных привело к треугольному множителю L, который разрежен в точности в той мере, что и нижний треугольник А.
Задача нахождения перестановки, минимизирующей заполнение при вычислении фактора Холецкого, является NPтрудной (т.к. вообще говоря, минимум должен вычисляться по всем n! перестановкам). Поэтому на практике используют эвристические алгоритмы, которые хотя и не гарантируют, что находят оптимальную перестановку, но, как правило, дают приемлемый результат.
Таким образом, при решении разреженной системы методом Холецкого можно выделить следующие этапы:
- Переупорядочивание – вычисление матрицы перестановки P;
- Символическое разложение – построение портрета матрицы L и выделение памяти под хранение ненулевых элементов;
- Численное разложение – вычисление значений матрицы L и размещение их в выделенной памяти.
- Обратный ход – решение двух треугольных систем уравнений.
Этапы 1 и 2 специфичны именно для разреженных матриц, тогда как этапы 3 и 4 выполняются для любых задач.
Ниже мы рассмотрим два известных алгоритма определения матрицы перестановки – методы минимальной степени и вложенных сечений.
Метод минимальной степени
Для формулирования метода минимальной степени нам потребуются некоторые сведения из теории графов.
Рассмотрим неориентированный граф G. Формально граф G можно рассматривать как упорядоченную пару двух множеств
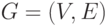
где 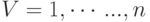 – множество вершин,
– множество вершин,  -множество связей между вершинами (ребер). Так как рассматриваемый граф – неориентированный, то множество E удовлетворяет свойству
-множество связей между вершинами (ребер). Так как рассматриваемый граф – неориентированный, то множество E удовлетворяет свойству

Пара вершин  называется смежной, если существует ребро, их соединяющее, т.е.
называется смежной, если существует ребро, их соединяющее, т.е.
Для любой вершины 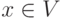 можно определить множество
можно определить множество  смежных ей вершин как
смежных ей вершин как
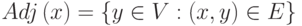
Мощность множества  называется степенью вершины
называется степенью вершины
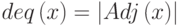
Граф, каждые две вершины которого соединены ребром, называется полным.
Подграф исходного графа – граф, содержащий некое подмножество вершин данного графа и некое подмножество инцидентных им рёбер.
Кликой в неориентированном графе называется подмножество вершин, каждые две из которых соединены ребром графа. Иными словами, это полный подграф первоначального графа.
Одной из форм задания графа 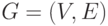 является матрица смежности
является матрица смежности 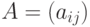 размера
размера  такая, что
такая, что
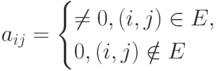
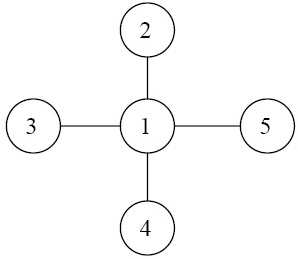
В нашем случае матрицу A системы линейных уравнений (7.41) можно рассмотреть как матрицу смежности соответствующего графа G(A), за исключением диагональных элементов, которым будут соответствовать петли. На рис. 7.19 приведен граф, соответствующий матрице из примера (7.42).
После того, как введены все необходимые определения, можно перейти к описанию алгоритма минимальной степени.
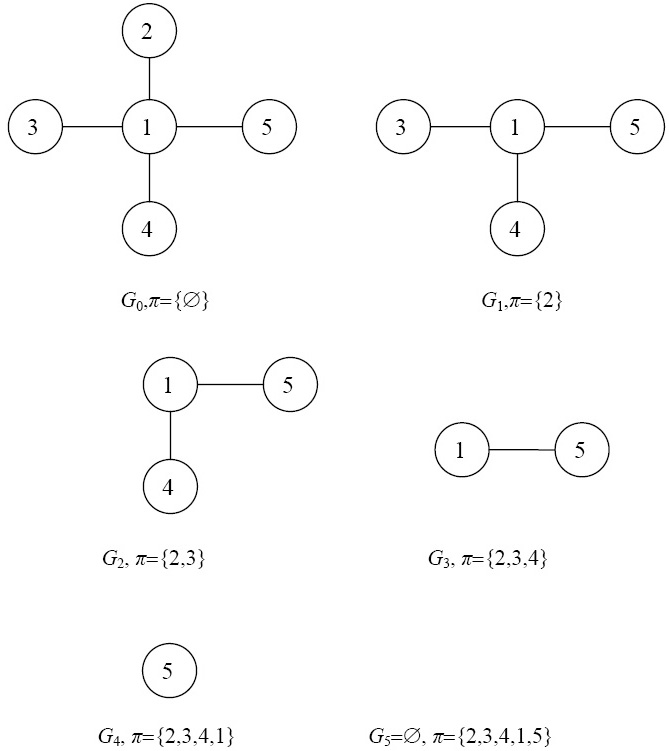
Пусть исходной матрице A из (7.41) соответствует граф G(A). Алгоритм минимальной степени строит последовательность графов исключения  , каждый их которых получен из предыдущего удалением вершины с минимальной степенью и созданием клики между всеми вершинами, которые были смежными с удаленной. В случае, когда вершин с минимальной степенью несколько, выбирается любая. Алгоритм продолжается до тех пор, пока в очередном графе есть вершины. По мере удаления вершин, их номер записывается в перестановку
, каждый их которых получен из предыдущего удалением вершины с минимальной степенью и созданием клики между всеми вершинами, которые были смежными с удаленной. В случае, когда вершин с минимальной степенью несколько, выбирается любая. Алгоритм продолжается до тех пор, пока в очередном графе есть вершины. По мере удаления вершин, их номер записывается в перестановку  , по которой впоследствии строится матрица перестановки P.
, по которой впоследствии строится матрица перестановки P.
В качестве примера работы алгоритма на рис. 7.20 приведена последовательность графов исключения и соответствующая перестановка  , порождаемая алгоритмом минимальной степени для задачи (7.42).
, порождаемая алгоритмом минимальной степени для задачи (7.42).
Полученная перестановка  ={2,3,4,1,5} соответствует матрице
={2,3,4,1,5} соответствует матрице
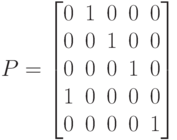
которая отличается от уже рассмотренной нами перестановки (7.44). Проверим ожидаемые свойства переупорядоченной матрицы: новая матрица системы уравнений, получаемая по формуле 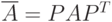 , будет
, будет
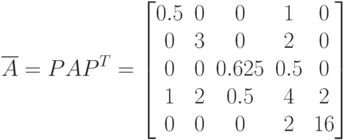 |
( 7.45) |
Фактор Холецкого, соответствующий данной матрице, будет (с точностью до  )
)
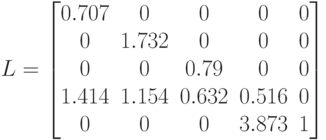
Видно, что при факторизации матрицы  не образуется порожденных элементов. Однако это не всегда выполняется, алгоритм лишь необходимым образом уменьшает количество порожденных элементов.
не образуется порожденных элементов. Однако это не всегда выполняется, алгоритм лишь необходимым образом уменьшает количество порожденных элементов.