|
поддерживаю выше заданые вопросы
|
Умножение разреженных матриц
Организация параллельных вычислений
Как и в методе исключения Гаусса, в данном алгоритме все вычисления сводятся к однотипным вычислительным операциям над строками матрицы L. Как результат, в основу параллельной реализации разложения может быть положен принцип распараллеливания по данным. В качестве базовой подзадачи можно принять тогда все вычисления, связанные с обработкой одной строки матрицы L.
Рассмотрим общую схему параллельных вычислений и возникающие при этом информационные зависимости между базовыми подзадачами.
При выполнении прямого хода метода необходимо осуществить (n–1) итерацию для получения нижней треугольной матрицы L. Выполнение итерации i,  , включает ряд последовательных действий. Прежде всего, в самом начале итерации необходимо вычислить диагональный элемент
, включает ряд последовательных действий. Прежде всего, в самом начале итерации необходимо вычислить диагональный элемент 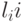 . Зная диагональный элемент, подзадачи выполняют вычисление i-го столбца матрицы L.
. Зная диагональный элемент, подзадачи выполняют вычисление i-го столбца матрицы L.
При выполнении обратного хода метода Холецкого подзадачи выполняют необходимые вычисления для нахождения значений сначала вспомогательного вектора y, а затем вектора неизвестных x. Как только какая-либо подзадача i,  , определяет значение своей переменной
, определяет значение своей переменной  (или
(или  ), это значение должно быть использовано всеми подзадачами с номерами k, где k>i при решении системы относительно y, и k<i при решении системы относительно x; подзадачи подставляют полученное значение новой неизвестной и выполняют корректировку значений для элементов вектора правой части.
), это значение должно быть использовано всеми подзадачами с номерами k, где k>i при решении системы относительно y, и k<i при решении системы относительно x; подзадачи подставляют полученное значение новой неизвестной и выполняют корректировку значений для элементов вектора правой части.
При использовании систем с общей памятью размер матрицы, описывающей систему линейных уравнений, является большим, чем число потоков (т.е., p<n). Следовательно, базовые подзадачи нужно укрупнить, объединив в рамках одной подзадачи несколько строк матрицы. Здесь также можно использовать циклическую схему распределения данных, аналогично методу Гаусса (см. п. 7.1.2).
Итак, проведя анализ последовательного варианта метод Холецкого, можно заключить, что распараллеливание возможно для следующих вычислительных процедур:
- вычисление диагонального элемента
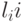 в соответствии с (7.13),
в соответствии с (7.13), - вычисление элементов i-го столбца в соответствии с (7.14),
- выполнение обратного хода в соответствии с (7.15), (7.16).
Оценим трудоемкость рассмотренного параллельного варианта метода Холецкого. Пусть  есть порядок решаемой системы линейных уравнений,
есть порядок решаемой системы линейных уравнений,  обозначает число потоков в программе.
обозначает число потоков в программе.
При разработке параллельного алгоритма все вычислительные операции, были распределены между потоками параллельной программы. Пусть  – время, необходимое на организацию и закрытие параллельной секции. Параллельная секция создается при каждом вычислении диагонального элемента, при вычислении элементов текущего столбца матрицы
– время, необходимое на организацию и закрытие параллельной секции. Параллельная секция создается при каждом вычислении диагонального элемента, при вычислении элементов текущего столбца матрицы  , а также на каждой итерации при решении двух систем с треугольными матрицами. Таким образом, общее число параллельных секций составляет 4n.
, а также на каждой итерации при решении двух систем с треугольными матрицами. Таким образом, общее число параллельных секций составляет 4n.
Следовательно, теоретическая оценка времеми, необходимого для решения системы, составит
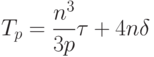
Результаты вычислительных экспериментов
Вычислительные эксперименты для оценки эффективности параллельного варианта блочного метода Холецкого проводились при стандартных условиях, указанных во введении. С целью формирования симметричной положительно определенной матрицы A размера  для тестовой системы уравнений диагональный элемент матрицы генерировался в диапазоне от n до 2n, остальные элементы генерировались в диапазоне от 0 до 1 (с учетом симметрии).
для тестовой системы уравнений диагональный элемент матрицы генерировался в диапазоне от n до 2n, остальные элементы генерировались в диапазоне от 0 до 1 (с учетом симметрии).
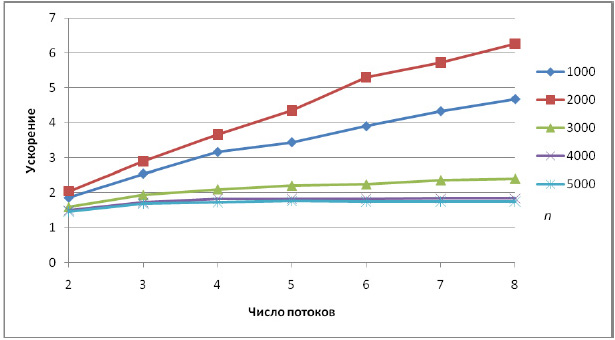
Результаты вычислительных экспериментов приведены в таблице 7.5 (время работы алгоритмов указано в секундах).
| Размер | 1 поток | Параллельный алгоритм | |||||||
|---|---|---|---|---|---|---|---|---|---|
| 2 потока | 4 потока | 6 потоков | 8 потоков | ||||||
| t | S | t | S | t | S | t | S | ||
| 1000 | 0,12 | 0,06 | 1,86 | 0,04 | 3,16 | 0,03 | 3,90 | 0,03 | 4,68 |
| 2000 | 1,07 | 0,52 | 2,04 | 0,29 | 3,66 | 0,20 | 5,30 | 0,17 | 6,26 |
| 3000 | 4,20 | 2,64 | 1,59 | 2,00 | 2,10 | 1,87 | 2,24 | 1,75 | 2,40 |
| 4000 | 10,11 | 6,76 | 1,50 | 5,54 | 1,83 | 5,54 | 1,83 | 5,49 | 1,84 |
| 5000 | 19,75 | 13,53 | 1,46 | 11,37 | 1,74 | 11,28 | 1,75 | 11,28 | 1,75 |
Как показывают эксперименты, алгоритм хоршо масштабируется для матриц размера не более 2000. Действительно, при таком размере матрицы А ее нижний треугольник (а только он и нужен для проведения расчетов в силу симметрии матрицы) целиком помещается в кэш-память компьютера. При больших размерах матрицы возрастает число кэш-промахов. Сгладить данный эффект и получить масштабируемый алгоритм нам поможет, как и в случае метода Гаусса, блочный подход к обработке данных.
Блочный алгоритм
Рассмотрим теперь, как и в п. 7.1.5, вычислительную процедуру, основанную на идее разбиения матрицы на блоки и ориентированную на эффективную работу с кэш-памятью. Разложение осуществляется путем переписывания исходной матрицы элементами искомого фактора Холецкого сверху вниз по блокам.
Первый шаг блочного алгоритма заключается в следующем. Пусть мы определили размер блока как r, тогда исходную матрицу A можно представить в виде
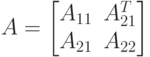
где 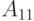 - подматрица матрицы А размера
- подматрица матрицы А размера  ,
, 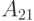 -размера
-размера 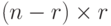 ,
, 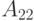 - размера
- размера  . Искомый фактор Холецкого также можно записать в блочном виде как
. Искомый фактор Холецкого также можно записать в блочном виде как
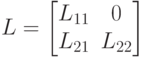
где 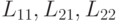 - соответствующего размера подматрицы фактора L.
- соответствующего размера подматрицы фактора L.
Рассмотрим теперь связь между блоками фактора и исходной матрицы. Используя соотношение (7.10), запишем
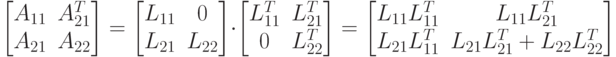
откуда получим
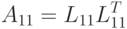 |
( 7.17) |
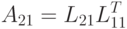 |
( 7.18) |
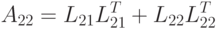 |
( 7.19) |
Используя данные матричные равенства, можно найти блоки 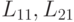 из искомого разложения.
из искомого разложения.
Блок 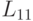 может быть получен с помощью обычного неблочного алгоритма, изложенного в п. 7.2.1, т.к. формула (7.17) соответствует разложению Холецкого для матрицы
может быть получен с помощью обычного неблочного алгоритма, изложенного в п. 7.2.1, т.к. формула (7.17) соответствует разложению Холецкого для матрицы 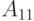 .
.
Далее, используя известный блок 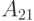 и найденный блок
и найденный блок 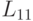 , из соотношения (7.18) можно найти блок
, из соотношения (7.18) можно найти блок 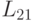 . Для этого потребуется решить r вспомогательных систем из r уравнений с одинаковой матрицей и разными правыми частями. Но так как матрица
. Для этого потребуется решить r вспомогательных систем из r уравнений с одинаковой матрицей и разными правыми частями. Но так как матрица 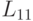 является треугольной, то решение одной системы потребует лишь
является треугольной, то решение одной системы потребует лишь 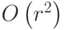 операций. Всего же для нахождения блока
операций. Всего же для нахождения блока 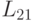 потребуется
потребуется 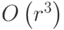 операций с плавающей точкой.
операций с плавающей точкой.
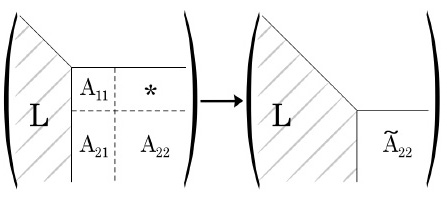
Следующий шаг алгоритма состоит в вычислении редуцированной матрицы 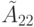 , при котором используется ставший известным блок
, при котором используется ставший известным блок 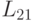 , блок
, блок 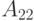 и соотношение (7.19),
и соотношение (7.19),
 |
( 7.20) |
Как следует из данной формулы, фактор Холецкого для матрицы 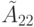 совпадает с искомым блоком
совпадает с искомым блоком 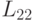 , и для его нахождения можно применить описанный алгоритм рекурсивно.
, и для его нахождения можно применить описанный алгоритм рекурсивно.
По построению матрица 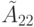 является симметричной положительно определенной, и при реализации алгоритма нет необходимости вычислять ее полностью, достаточо вычислить в соответствии с формулой (7.20) ее нижний треугольник.
является симметричной положительно определенной, и при реализации алгоритма нет необходимости вычислять ее полностью, достаточо вычислить в соответствии с формулой (7.20) ее нижний треугольник.
Процесс блочной факторизации проиллюстрирован на рис. 7.7.
Известно [8], что данная вычислительная процедура включает в себя

операций, как и другие возможные реализации метода Холецкого; при этом вклад матричных операций в общее число действий (аналогично блочному LU-разложению) аппроксимируется величиной
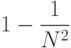
где 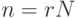 . Отсюда следует, что матричные операции, в частности, в соответствии с формулой (7.20), будут составлять большую часть вычислений, и к реализации матричного умножения нужно подойти с особой тщательностью. В данном случае для проведения операции матричного умножения целесообразно воспользоваться блочной схемой умножения матриц, выбрав для этого свой размер блока, меньший r. Описание блочного алгоритма умножения матриц см., например, в [16].
. Отсюда следует, что матричные операции, в частности, в соответствии с формулой (7.20), будут составлять большую часть вычислений, и к реализации матричного умножения нужно подойти с особой тщательностью. В данном случае для проведения операции матричного умножения целесообразно воспользоваться блочной схемой умножения матриц, выбрав для этого свой размер блока, меньший r. Описание блочного алгоритма умножения матриц см., например, в [16].
Рассмотрим теперь способы параллельной реализации блочного метода Холецкого. После внимательного анализа данного алгоритма можно заключить, что распараллеливание возможно для следующих вычислительных процедур:
- вычисление блока
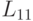 в соответствии с (7.17) (параллельная версия неблочного алгоритма);
в соответствии с (7.17) (параллельная версия неблочного алгоритма); - вычисление блока
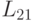 в соответствии с (7.18) (параллельное решение набора систем линейных уравнений с треугольной матрицей);
в соответствии с (7.18) (параллельное решение набора систем линейных уравнений с треугольной матрицей); - выполнение матричного умножения в соответствии с (7.20);
- выполнение обратного хода в соответствии с (7.15), (7.16).
В силу большей трудоемкости прямого хода алгоритма (т.е. собственно разложения) эффективность параллельного блочного алгоритма будет определяться эффективностью распараллеливания матричных операций, составляющих основную долю операция прямого хода.
Результаты вычислительных экспериментов
Сначала приведем время работы блочного алгоритма Холецкого и его исходного неблочного варианта (время работы t указано в секундах, столбец, отмеченный прочерком, соответствует неблочному алгоритму).
| n | Время работы t, c | |||||
|---|---|---|---|---|---|---|
| --- | r=10 | r=20 | r=50 | r=100 | r=200 | |
| 1000 | 0,11 | 0,28 | 0,21 | 0,16 | 0,16 | 0,15 |
| 2000 | 1,05 | 2,62 | 1,99 | 1,39 | 1,23 | 1,09 |
| 3000 | 4,16 | 9,81 | 7,25 | 4,84 | 4,17 | 3,71 |
| 4000 | 10,00 | 25,05 | 18,22 | 11,74 | 10,00 | 9,63 |
| 5000 | 19,59 | 49,23 | 35,82 | 23,24 | 20,39 | 20,22 |
Из таблицы следует, что блочный алгоритм значительно проигрывает неблочному при малых размерах блока факторизации, и почти сравнивается по скорости при увеличении размера блока. Данный факт объясняется тем, что при реализации формулы (7.20) мы использовали алгоритм умножения матриц по определению. Посмотрим, что изменится, если применить блочный алгорим матричного умножения, который более эффективно использует кэш-память.
Для выбора оптимального размера блока при выполнении матричного умножения нами были проведены эксперименты при размерах блока от  до
до  с шагом 5. Лучшие результаты приведены в таблице ниже.
с шагом 5. Лучшие результаты приведены в таблице ниже.
| n | Время работы t | |||
|---|---|---|---|---|
| --- | r=50 (25x50) | r=100 (25x50) | r=200 (10x200) | |
| 1000 | 0,12 | 0,11 | 0,12 | 0,13 |
| 2000 | 1,07 | 0,78 | 0,80 | 0,83 |
| 3000 | 4,20 | 2,57 | 2,61 | 2,64 |
| 4000 | 10,11 | 5,98 | 5,99 | 6,10 |
| 5000 | 19,75 | 12,57 | 11,50 | 11,84 |
Ситуация значительно улучшилась – теперь блочный алгоритм показывает такое же быстродействие на матрицах малого размера (которые полностью умещаются в кэшпамять), и значительно обгоняет неблочный на матрицах большого размера. При этом время, затрачиваемое алгоритмом, является примерно одинаковым для любых размеров блоков факторизации r (отличие есть лишь в сотых долях секунды).
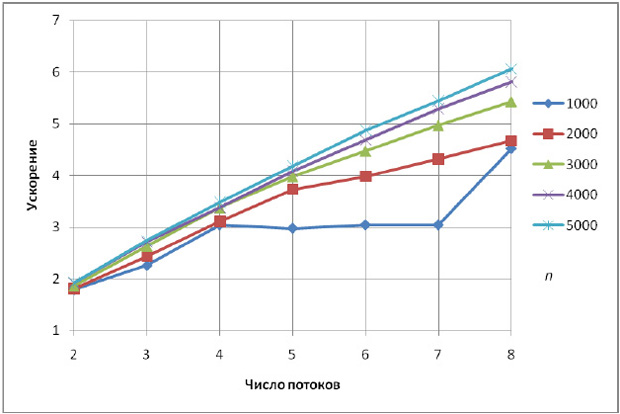
Осталось убедиться в том, что наше решение будет масштабируемым – проведем разложение с использованием параллельного блочного алгоритма с размером блока факторизации 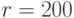 и блоком матричного умножениия
и блоком матричного умножениия 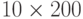 в соответствии с описанной схемой распараллеливания. Как уже обсуждалось ранее, время работы последовательной программы и параллельной программы, запущенной в один поток, будет разным. Этим объясняются разные времена работы алгоритмов, приведенных в табл. 7.8 и табл. 7.9.
в соответствии с описанной схемой распараллеливания. Как уже обсуждалось ранее, время работы последовательной программы и параллельной программы, запущенной в один поток, будет разным. Этим объясняются разные времена работы алгоритмов, приведенных в табл. 7.8 и табл. 7.9.
| n | 1 поток | Параллельный алгоритм | |||||||
|---|---|---|---|---|---|---|---|---|---|
| 2 потока | 4 потока | 6 потоков | 8 потоков | ||||||
| t | S | t | S | t | S | t | S | ||
| 1000 | 0,14 | 0,08 | 2,15 | 0,05 | 3,77 | 0,05 | 4,98 | 0,03 | 4,98 |
| 2000 | 0,87 | 0,48 | 1,90 | 0,28 | 3,52 | 0,22 | 4,84 | 0,19 | 5,80 |
| 3000 | 2,79 | 1,50 | 1,95 | 0,83 | 3,55 | 0,62 | 4,94 | 0,51 | 6,10 |
| 4000 | 6,43 | 3,35 | 1,94 | 1,90 | 3,51 | 1,37 | 4,91 | 1,11 | 6,03 |
| 5000 | 12,39 | 6,44 | 1,94 | 3,56 | 3,52 | 2,54 | 4,87 | 2,04 | 6,05 |
Как показывают эксперименты, блочный алгоритм хорошо масштабируется – ускорения достигает значения 6 для 8-и поточной программы.
Метод прогонки
Одним из частных (но, тем не менее, часто встречающихся) видов системы (7.2) является система
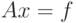
с ленточной матрицей A. Матрица A называется ленточной, когда все ее ненулевые элементы находятся вблизи главной диагонали, т.е. 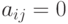 , если
, если 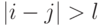 , где
, где 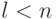 . Число l называется шириной ленты. Примером является трехдиагональная матрица (при l=1) вида:
. Число l называется шириной ленты. Примером является трехдиагональная матрица (при l=1) вида:
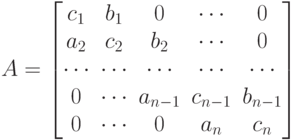
Матрицы такого вида возникают, например, при решении задачи сплайнинтерполяции [1].
Рассмотрим метод прогонки, применимый для решения систем с трехдиагональной матрицей. Предположим, что имеет место соотношение
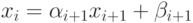 |
( 7.21) |
с неопределенными коэффициентами 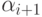 и
и 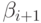 и подставим выражение
и подставим выражение 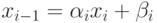 в i-e уравнение системы:
в i-e уравнение системы:
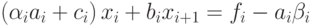
Сравнивая полученное выражение с (7.21), находим
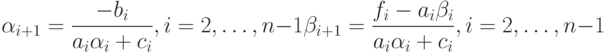 |
( 7.22) |
Из первого уравнения системы
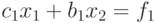
находим
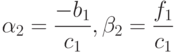
Зная 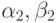 и переходя от i к
и переходя от i к  в формулах (7.22), определим
в формулах (7.22), определим 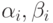 для всех
для всех 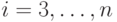 .
.
Определим 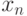 из последнего уравнения системы и условия (7.21) при
из последнего уравнения системы и условия (7.21) при  .
.
 |
( 7.23) |
Решив систему из двух уравнений с двумя неизвестными, находим
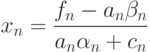
После того, как значение 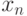 найдено, определяем все остальные значения
найдено, определяем все остальные значения  в обратном порядке, используя формулу (7.21). Соберем теперь все формулы прогонки и запишем их в порядке применения.
в обратном порядке, используя формулу (7.21). Соберем теперь все формулы прогонки и запишем их в порядке применения.
Прямой ход:
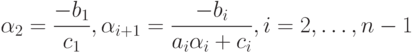 |
( 7.24) |
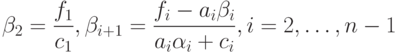
Обратный ход:
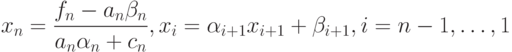 |
( 7.25) |
Известно [4], что для вычислительной устойчивости метода прогонки необходимо выполнение условия диагонального преобладания

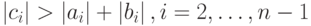
Оценим трудоемкость метода прогонки. При выполнении прямого хода по формулам (7.24) потребуется 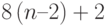 операций. Для выполнения обратного хода по формулам (7.25) потребуется
операций. Для выполнения обратного хода по формулам (7.25) потребуется 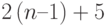 операций. Таким образом, общее число операций можно оценить величиной
операций. Таким образом, общее число операций можно оценить величиной
 |
( 7.26) |
а время решения системы методом прогонки при больших n будет определяться как
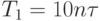
где  время выполнения одной операции.
время выполнения одной операции.
Метод встречной прогонки и его распараллеливание
Рассмотренный в предыдущем пункте метод прогонки, определяемый соотношениями (7.24) и (7.25), при котором определение  происходит последовательно справа налево, называют правой прогонкой. Аналогично выписываются формулы левой прогонки.
происходит последовательно справа налево, называют правой прогонкой. Аналогично выписываются формулы левой прогонки.
Прямой ход:
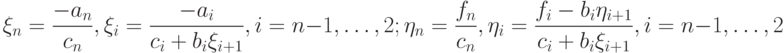 |
( 7.27) |
Обратный ход:
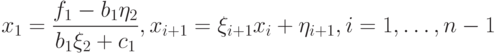 |
( 7.28) |
В самом деле, предполагая, что 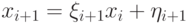 , исключим из i-го уравнения системы переменную
, исключим из i-го уравнения системы переменную 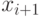 , получим
, получим
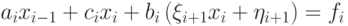
или
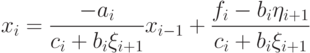
Сравнивая с формулой 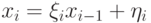 , получим расчетные формулы (7.27). Значение
, получим расчетные формулы (7.27). Значение  находим из первого уравнения и условия
находим из первого уравнения и условия 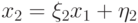 , затем, используя условие
, затем, используя условие 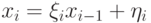 и известные коэффициенты
и известные коэффициенты  можно найти все остальные значения неизвестных.
можно найти все остальные значения неизвестных.
Нетрудно видеть, что трудоемкость левой прогонки составляет также  .
.
Комбинация левой и правой прогонок дает метод встречной прогонки, который допускает распараллеливание на два потока. Разделим систему между двумя потоками – первый будет оперировать уравнениями с номерами 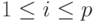 , второй – уравнениями
, второй – уравнениями 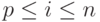 , где
, где  .
.
При параллельном решении системы в первом потоке по формулам (7.22) вычисляются прогоночные коэффициенты 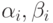 при
при 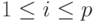 а во втором потоке по формулам (7.27) находятся
а во втором потоке по формулам (7.27) находятся  при
при 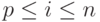 . При
. При 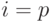 проводится сопряжение решений в форме (7.25) и (7.28): находим значение
проводится сопряжение решений в форме (7.25) и (7.28): находим значение 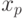 из системы
из системы
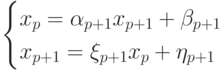
Найдя указанное значение, в первом потоке можно по формуле (7.25) найти все xi, при 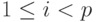 , а во втором - по формуле (7.28) – все
, а во втором - по формуле (7.28) – все  , при p<i\leq n.
, при p<i\leq n.
Трудоемкость метода параллельной встречной прогонки можно оценить как

где  – время, необходимое на организацию и закрытие параллельной секции. Следует отметить, что расчеты и при прямом, и при обратном ходе производятся независимо, теоретическое ускорение здесь должно быть равно двум.
– время, необходимое на организацию и закрытие параллельной секции. Следует отметить, что расчеты и при прямом, и при обратном ходе производятся независимо, теоретическое ускорение здесь должно быть равно двум.