НОУ ИНТУИТ | Введение в теорию программирования. Функциональный подход. Лекция 11: Абстрактные машины и категориальная комбинаторная логика

Учитесь и получайте официальные документы БЕСПЛАТНО. Вы можете поддержать наш проект.

Регистрация Вход

Твой путь к знаниям!

Национальный исследовательский ядерный университет «МИФИ»

Опубликован: 09.01.2004 | Доступ: свободный | Студентов: 3808 / 327 | Оценка: 4.02 / 3.77 | Длительность: 10:03:00

ISBN: 978-5-9556-0009-3

Тема: Программирование

Специальности: Программист, Архитектор программного обеспечения

|

Вам нравится? Нравится 27 студентам

| Поделиться |

Поддержать курс

| Скачать электронную книгу

Перейдем к обсуждению теоретического фундамента, на котором основана категориальная абстрактная машина, а конкретно, к формальной системе категориальной комбинаторной логики (ККЛ).

Как уже отмечалось, своим названием категориальная абстрактная машина обязана тому обстоятельству, что множество ее возможных состояний принадлежит пространству так называемых декартово замкнутых категорий (или, сокращенно, д.з.к.).

Формальная система с декартово замкнутыми категориями должна удовлетворять следующим условиям:

определена функция тождества или тождественное преобразование (имеющее в комбинаторной логике аналог в форме комбинатора тождества I );
определена операция композиции или построения сложной функции (имеющая в комбинаторной логике аналог в форме комбинатора тождества B );
определена операция образования упорядоченной пары объектов < . , . >;
определена операция взятия первого элемента из упорядоченной пары объектов;
определена операция взятия второго элемента из упорядоченной пары объектов;
определена операция преобразования терма из алгебраической формы в аппликативную;
определена операция аппликации или применения функции к аргументу.

Проанализируем смысл сформулированных условий для категорий.

Условия существования тождественного преобразования и построения сложных функций являются основополагающими и необходимы для формирования категорий произвольного типа.

Условия существования операции образования упорядоченной пары объектов, а также операций взятия первого и второго элементов из упорядоченной пары необходимы для построения декартовых категорий, т.е. категорий, оснащенных операцией прямого (или, иначе, декартова) произведения и соответствующих ему проекций.

Наконец, условия существования операций аппликации и преобразования терма из алгебраической формы в аппликативную необходимы для формирования декартово замкнутых категорий .

Заметим, что последняя операция называется каррированием, а обратная ей - декаррированием по имени основоположника комбинаторной логики Х. Карри (Haskell B. Curry).

Кроме перечисленных выше условий, для построения декартовых категорий необходимо дополнительно потребовать существования функционального пространства или операции экспоненцирования.

Для реализации категориального расширения комбинаторной логики (известного также как категориальная комбинаторная логика, или, сокращенно, ККЛ), добавим к известным нам комбинаторам

(I) Ia = a; 
(K) Кab = a;
(S) Sabc = ac(bc); 
(B) Babc = a(bc); 
(C) Cabc = acb

следующие комбинаторы, выступающие в роли "машинных инструкций" категориальной абстрактной машины:

$(D) D = \lambda xy.[x,y] = \lambda xyr.rxy; \\ (S) S = CIS; \\ ( \Lambda ) \Lambda = \lambda x.(\lambda z.x[y,z]); \\ (') ' = K = \lambda x.(\lambda y.x).$

Заметим, что характеристическое соотношение ( D ) представляет собой операцию образования упорядоченной пары, соотношение ( $\Lambda$ ) - каррирование, а соотношение ( ' ), ранее известное нам как характеристика комбинатора-канцелятора K - операцию взятия первой проекции для упорядоченной пары элементов, которую можно также понимать как цитирование.

Продолжим построение формальной системы категориальной комбинаторной логики.

Рассмотрим семантический аспект данной системы, основываясь на функции вычисления значения выражения категориальной комбинаторной логики, соотнесенной, вообще говоря, с той или иной средой.

Введем одноместную функцию вычисления значения выражения для произвольного выражения, которую обозначим как || ||. Скажем, значение терма M в таком случае будет иметь вид || M ||.

Далее добавим бесконечное множество комбинаторов n! со следующей семантической характеристикой: ||n|| = n!.

Продолжим семантические равенства следующим соотношением, характеризующим значения констант: ||с|| = 'с.

Как следует из приведенного соотношения, для вычисления значения константы используется комбинатор цитирования (что хорошо согласуется с практикой, принятой в языках функционального программирования, в частности в языке LISP).

Значения упорядоченной пары и ламбда-абстракции, как выясняется, задаются с помощью ранее рассмотренных комбинаторов S и 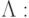$\Lambda:$

$||M,N|| = S [||M||,||N||]; \\ ||\lambda x.M|| = \Lambda (M).$

Продолжим построение формальной системы категориальной комбинаторной логики.

Заметим, что благодаря введению дополнительных комбинаторов

$(D) D = \lambda xy.[x,y] = \lambda xyr.rxy; \\ (S) S = CIS; \\ (\Lambda ) \Lambda = \lambda x.(\lambda z.x[y,z]); \\ (') ' = K = \lambda x.(\lambda y.x)$

перечисленные выше синтактико-семантические соотношения сводятся к чисто синтаксическим равенствам, которые имеют следующий вид:

$0! [x,y] = y; \\ (n+1)! [x,y] = n!x; \\ S[x,y]z = xz(yz);\Lambda (x)yz = x[y,z].$

Отметим, что последние два соотношения, означающие, соответственно, декаррирование и каррирование, необходимы для завершения перехода от формальной системы комбинаторной логики к формальной системе ККЛ.

Продолжим построение формальной системы категориальной комбинаторной логики.

Для того чтобы формализация приняла более строгий и удобный вид, необходимо ввести в рассмотрение двухместный комбинатор образования пары, который определяется ламбда-выражением следующего вида:

$< . , . > = \lambda t.[ . t, . t].$

При этом комбинаторная характеристика вновь введенного комбинатора образования пары имеет следующий вид:

$<f,g> = \lambda t.\lambda z.(ft)(gt) = \lambda t.[ft,gt].$

Кроме того, комбинатор образования пары характеризуется следующим семантическим равенством:

||M,N|| = <||[M]||,||[N]||>.

Продолжим построение формальной системы категориальной комбинаторной логики.

После задания операции образования упорядоченной пары функций для завершения формализации операции прямого или декартова произведения необходимо определить операции взятия первого и второго элементов упорядоченной пары, или первой и второй проекций.

Согласно общепринятой алгебраической практике, оснастим вновь введенную операцию декартова произведения комбинаторами первой и второй проекций с комбинаторными характеристиками следующего вида:

Fst = CIK = (n+1)!
Snd = CI(KI) = (0)!

Отметим, что вновь введенные комбинаторы Fst для первой проекции и Snd для второй проекции имеют следующие характеристические соотношения:

Fst [x,y] = x;
Snd [x,y] = y;
<x,y> z = [xz,yz].

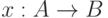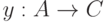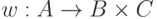Последнее соотношение определяет связь между комбинатором образования упорядоченной пары и так называемой парой функций, т.е. такой функцией, которая в результате дает совокупность результатов своих функций-компонентов $x:A \rightarrow B$ и $y:A \rightarrow C$ в виде функции $w:A \rightarrow B \times C$ .

Продолжим построение формальной системы категориальной комбинаторной логики.

Заметим, что введенная система комбинаторов Fst, Snd, (n+1)!, 0!, S, $\Lambda$ является избыточной.

Избыточность системы комбинаторов устраняется введением комбинатора композиции

o = B,

который принимается тождественно равным ранее определенному комбинатору композиции B.

Теперь явно введем комбинатор аппликации 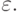$\varepsilon.$

Выведем соотношения, которые позволят устранить избыточность системы комбинаторов:

$S(xyt) = xt(yt) = \varepsilon [xt,yt] = (\varepsilon o<x,y>)t.$

Отсюда,

$(i) S = \lambda xy.(\varepsilon o<x,y>).$

Положим Fstⁿ⁺¹=FstoFstⁿ, для n>1 и Fst¹=Fst. Тогда получим, что

(ii)	n!=SndoFstn, для n>0, а 0!=Snd.

Завершим построение формальной системы категориальной комбинаторной логики.

С учетом устранения избыточных комбинаторов из рассматриваемой формальной системы, получим окончательный перечень характеристических соотношений категориальной комбинаторной логики:

$(ass) (xoy) z = x(yz); \\ (fst) Fst[x,y] = x; \\ (snd) Snd[x,y] = y; \\ (dpair) <x,y>z = [xz,yz]; \\ (ac) \varepsilon [\Lambda (x)y,z] = x[y,z]; \\ (quote) ('x)y = x.$

Заметим, что соотношение ( ass ) устанавливает связь аппликации и композиции, соотношение ( dpair ) - спаривания и формирования совокупности, а соотношение ( ac ) - каррирования и апплицирования.

Напомним, что соотношения ( fst ) и ( snd ) характеризуют операции взятия первой и второй проекций для упорядоченной пары объектов, а ( quote ) - цитирование.

Приведенные соотношения ( ass ), ( fst ), ( snd ), ( dpair ), ( ac ) и ( quote ) адекватно, то есть полно и непротиворечиво, формализуют систему категориальной комбинаторной логики.

Для более подробного самостоятельного ознакомления с тематикой лекции рекомендуется следующий список источников: [31,51,61,62].

Дальше >>

Авторизоваться

Введение в теорию программирования. Функциональный подход

Абстрактные машины и категориальная комбинаторная логика

Вопросы и ответы