Категориальная абстрактная машина
Итак, требуется построить вариант формальной системы комбинаторной логики для моделирования семантики вычислений.
Под вычислениями будем понимать трансляцию конструкций, которые заданы на языке программирования, в код категориальной абстрактной машины (возможно, с использованием некоторого промежуточного кода ) с последующим означиванием результирующего кода в той или иной среде.
Означивание кода категориальной абстрактной машины производится с помощью функции вычисления значения.
При такой постановке задачи необходимо принять во внимание ряд ранее сформулированных условий, в частности:
- условия, необходимые для построения формальной системы декартово замкнутых категорий (или, сокращенно, д.з.к.), рассмотренные нами в ходе предыдущей лекции;
- характеристические равенства, которые определяют поведение операторов, задающих денотационную семантику языка функционального программирования, в том числе и инструкций категориальной абстрактной машины.
Напомним условия, необходимые для построения формальной системы д.з.к.
Формальная система с д.з.к. должна удовлетворять следующим условиям:
- определена функция тождества, или тождественное преобразование (имеющее в комбинаторной логике аналог в форме комбинатора тождества I );
- определена операция композиции или построения сложной функции (имеющая в комбинаторной логике аналог в форме комбинатора тождества B );
- определена операция образования упорядоченной пары объектов < . , . > ;
- определена операция взятия первого элемента из упорядоченной пары объектов;
- определена операция взятия второго элемента из упорядоченной пары объектов;
- определена операция преобразования терма из алгебраической формы в аппликативную;
- определена операция аппликации или применения функции к аргументу.
Заметим, что выполнение перечисленных условий необходимо для того, чтобы обеспечить принадлежность состояний категориальной абстрактной машины пространству д.з.к..
Напомним характеристические равенства, которые определяют поведение операторов, задающих синтаксис и семантику языка инструкций категориальной абстрактной машины:
![(ass) (xoy)z = x(yz);
\\
(fst) Fst[x,y] = x;
\\
(snd) Snd[x,y] = y;
\\
(dpair) <x,y>z = [xz,yz];
\\
(ac) \varepsilon [\Lambda (x)y,z] = x[y,z];
\\
(quote) ('x)y = x.](/sites/default/files/tex_cache/5cb130e572b8332e4821ddf116dd8764.png)
Соотношение ( ass ) устанавливает связь аппликации и композиции, соотношения ( fst ) и ( snd ) – первой и второй проекций и операции образования упорядоченной пары, соотношение ( dpair ) – спаривания и формирования совокупности, соотношение ( ac ) – каррирования и апплицирования, а ( quote ) характеризует цитирование.
Заметим, что данный перечень характеристических соотношений категориальной комбинаторной логики является базисным и получен с учетом устранения избыточных комбинаторов из рассматриваемой формальной системы.
Завершив этап предварительной подготовки необходимого набора соотношений, перейдем непосредственно к реализации поставленной задачи формализации процедуры трансляции функциональной программы.
Схема процедуры трансляции текста программы на языке функционального программирования в результирующую последовательность инструкций категориальной абстрактной машины является многоэтапной и включает следующие стадии:
- преобразование текста программы на языке функционального программирования в соответствующее выражение ламбда-исчисления;
- преобразование полученного выражения ламбда-исчисления в так называемый (промежуточный) код де Брейна (de Brujin);
- преобразование полученного кода де Брейна в терм категориальной комбинаторной логики ;
- преобразование полученного терма категориальной комбинаторной логики в последовательность инструкций категориальной абстрактной машины ;
- выполнение результирующей последовательности инструкций категориальной абстрактной машины с означиванием в среде вычислений.
Подчеркнем, что собственно последовательность инструкций категориальной абстрактной машины (или, сокращенно, КАМ-код ) еще не является конечной целью нашего исследования.
Итогом процедуры трансляции является выполнение результирующей последовательности инструкций категориальной абстрактной машины с означиванием в зависимости от среды вычислений.
Первый этап процедуры трансляции, а именно, преобразование текста программы на языке функционального программирования в соответствующее выражение ламбда-исчисления, был достаточно подробно рассмотрен нами ранее, в ходе изучения синтаксиса языка программирования SML в сопоставлении с синтаксисом ламбда-исчисления.
Рассмотрим более подробно второй этап процедуры трансляции, который состоит в преобразовании полученного выражения ламбда-исчисления в так называемый (промежуточный) код де Брейна, названный так по имени его создателя. Смысл перехода к коду де Брейна состоит в унификации записи и ликвидации коллизии обозначений переменных в ламбда-термах.
Числом де Брейна называется глубина связывания переменной (которое понимается как количество ламбда-абстракций, находящихся в ламбда-терме до данной переменной) без единицы.
При трансляции текста программы на языке функционального программирования в код де Брейна производятся следующие преобразования:
- числа де Брейна, замещающие переменные ламбда-термов, заменяются соответствующими комбинаторами n, рассмотренными в ходе предыдущей лекции;
- операция аппликации заменяется комбинатором S;
- операция абстракции заменяется комбинатором
![\Lambda = \lambda x.(\lambda z.x[y,z])](/sites/default/files/tex_cache/ea9dc47c51c4f3be8c13da26c4e70512.png) ;
; - операция цитирования (в случае наличия в ламбда-терме констант) заменяется комбинатором цитирования
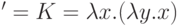 .
.
Проиллюстрируем кодирование ламбда-терма по де Брейну следующим примером. Пусть требуется закодировать ламбда-терм следующего вида:
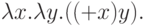
В результате получаем код де Брейна следующего вида:

В наших рассуждениях неоднократно использовалось понятие среды вычислений. Среда имеет важнейшее значение в теории и практике языков программирования, поскольку она определяет условия для выполнения той или иной программы в зависимости от характеристик компьютера, операционной системы, транслятора и другого окружения, в котором программа функционирует. Из истории языков программирования естественным образом следует, что в ходе эволюции программных систем среда изменялась в сторону повышения адаптивности и универсальности. Пожалуй, апогеем развития современных вычислительных сред является изучаемая в курсе технологическая платформа Microsoft .NET.
Формализуем понятие среды вычислений применительно к категориальной абстрактной машине.
При кодировании ламбда-выражений по де Брейну среда вычислений понимается как конечное упорядоченное множество пар вида
(<переменная>, <значение>).
При трансляции ламбда-терма в код де Брейна, который представляет собой пару вида (<терм де Брейна>, <среда>) в соответствии с характеристическими равенствами
![0![x,y] = y;
\\
(n+1)![x,y] = n!x;
\\
S[x,y] z = xz(yz);\Lambda (x)yz = x[y,z];](/sites/default/files/tex_cache/185123bb4db7c108d487b30e52228cc1.png)
среда вырождается в пустую и обозначается как "( )", а значения переменных явным образом присутствуют в результирующем коде.
Рассмотрим следующий этап процедуры трансляции, который состоит в преобразовании полученного кода де Брейна в выражение категориальной комбинаторной логики.
Переход от кода де Брейна к терму категориальной комбинаторной логики выполняется на основе известных характеристических равенств:
![(ass) (xoy)z = x(yz);
\\
(fst) Fst[x,y] = x;
\\
(snd) Snd[x,y] = y;
\\
(dpair) <x,y>z = [xz,yz];
\\
(ac) \varepsilon [\Lambda (x)y,z] = x[y,z];
\\
(quote) ('x)y = x.](/sites/default/files/tex_cache/5cb130e572b8332e4821ddf116dd8764.png)
Таким образом, в результате данного этапа трансляции получается "программа" в форме выражений категориальной комбинаторной логики, в значительной мере схожим с языком программирования.
При этом список " инструкций " "языка программирования" категориальной комбинаторной логики имеет следующий вид ("команды" разделены пробелами и указаны без кавычек):

