|
Возможна ли разработка приложения на Octave с GUI? |
Обработка результатов эксперимента. Метод наименьших квадратов
Пример 11.3. В результате эксперимента получена табличная зависимость 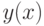 (см. табл. 11.5). Подобрать аналитические зависимости
(см. табл. 11.5). Подобрать аналитические зависимости  и
и 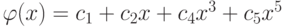 методом наименьших квадратов. Пользуясь значением индекса корреляции выбрать наилучшую из них, с помощью которой вычислить ожидаемое значение в точках 1, 2.5, 4.8. Построить графики экспериментальных точек, подобранных зависимостей. На графиках отобразить рассчитанные значения в точках 1, 2.5, 4.8.
методом наименьших квадратов. Пользуясь значением индекса корреляции выбрать наилучшую из них, с помощью которой вычислить ожидаемое значение в точках 1, 2.5, 4.8. Построить графики экспериментальных точек, подобранных зависимостей. На графиках отобразить рассчитанные значения в точках 1, 2.5, 4.8.
Как рассматривалось ранее, решать задачу подбора параметров полинома методом наименьших квадратов в Octave можно тремя способами.
- Сформировать и решить систему уравнений (11.3).
- Решить задачу оптимизации (11.1).
В случае полинома
 подбираемые коэффициенты
подбираемые коэффициенты  будут входить в функцию (11.1) линейным образом и не должно возникнуть проблем при решении задачи оптимизации с помощью функции
будут входить в функцию (11.1) линейным образом и не должно возникнуть проблем при решении задачи оптимизации с помощью функции  .
. - Использовать функцию
 .
.
увеличить изображение
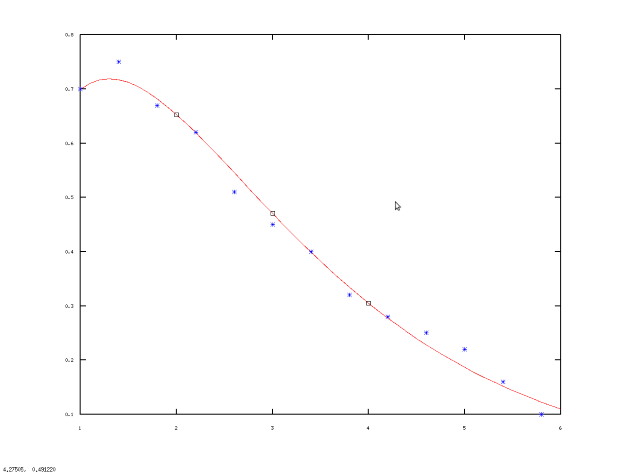
Рис. 11.3. График к примеру 11.2: экспериментальные точки и подобранная методом наименьших квадратов зависимость
| x | -2 | -1,3 | -0,6 | 0,1 | 0,8 | 1,5 | 2,2 | 2,9 | 3,6 | 4,3 | 5 | 5,7 | 6,4 |
| y | -10 | -5 | 0 | 0,7 | 0,8 | 2 | 3 | 5 | 8 | 30 | 60 | 100 | 238 |
Чтобы продемонстрировать использование всех трёх методов для подбора  воспользуемся функцией
воспользуемся функцией  , для формирования коэффициентов функции
, для формирования коэффициентов функции 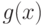 сформируем и решим систему уравнений (11.3), а функцию
сформируем и решим систему уравнений (11.3), а функцию 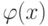 будем искать с помощью функции
будем искать с помощью функции  .
.
Для формирования подбора коэффициентов функции  сформируем систему уравнений. Составим функцию
сформируем систему уравнений. Составим функцию  . После дифференцирования
. После дифференцирования  по
по 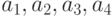 и
и 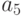 система линейных алгебраических уравнений для вычисления параметров
система линейных алгебраических уравнений для вычисления параметров  примет вид:
примет вид:
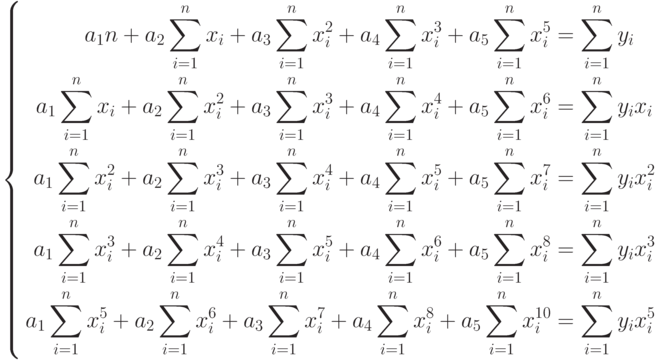 |
( 11.21) |
Решив систему (11.21), найдём коэффициенты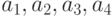 и
и 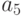 функции
функции .
.
Для поиска функциональной зависимости вида 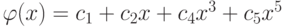 необходимо будет найти такие значения
необходимо будет найти такие значения  которых функция
которых функция
 |
( 11.22) |
принимала бы наименьшее значение.
После вывода необходимых формул приступим к реализации в Octave. Текст программы с очень подробными комментариями приведён в листинге 11.4.
% Функция для подбора зависимости fi(x) методом наименьших квадратов. function s=f_mnk(c) % Переменные x, y являются глобальными, используются в % функции f_mnk и главной функции. global x; global y; % Формирование суммы квадратов отклонений (11.22). s =0; for i =1: length(x) s=s+(y(i)-c(1)-c(2)*x(i)-c(3)*x(i)^3_c(4)*x(i)^5)^2; end end % Главная функция ———————————— global x; global y; % Определение координат экспериментальных точек x=[-2 -1.3 -0.6 0.1 0.8 1.5 2.2 2.9 3.6 4.3 5 5.7 6.4]; y=[-10 -5 0 0.7 0.8 2 3 5 8 30 60 100 2 3 8]; z =[1 2.5 4.8] % Подбор коэффициентов зависимости f(x) (полинома пятой степени) % методом наименьших квадратов, используя функцию polyfit. % Коэффициенты полинома будут хранится в переменной B. B=polyfit(x, y, 5) % Формирование точек для построения графиков подобранных функций. X1= -2:0.1:6.5; % Вычисление ординат точек графика первой функции f(x). Y1=polyval (B, X1); % Формирование системы (11.21) для подбора функции g(x). Здесь GGL — % матрица коэффициентов, H — вектор правых частей системы (11.21), % G — первые 4 строки и 4 столбца матрицы коэффициентов, G1 — пятый % столбец матрицы коэффициентов, G2 — пятая строка матрицы коэфф–тов. for i = 1:4 for j =1:4 G(i, j)= sum(x.^(i+j-2)); endfor endfor for i = 1:4 G1(i)= sum(x.^(i+5)); H(i)= sum(y.*x.^(i-1)); endfor for i =1:4 G2(i)= sum(x.^(i+4)); endfor G2(5)= sum(x.^10); % Формирование матрицы коэффициентов системы (11.21) из матриц % G, G1 и G2. GGL=[G G1’; G2] H(5)= sum(y.*x.^5); % Решение системы (11.21) методом обратной матрицы и % формирование коэффициентов А функции g(x). A=inv(GGL)*H’ % Подбор коэффициентов зависимости fi(x) методом наименьших квадратов, % используя функцию sqp. Коэффициенты функции будут хранится в перемен-% ной C. Задание начального значения вектора С, при неправильном его опре-% делении, экстремум функции может быть найден неправильно. C = [2; 1; 3; 1]; % Поиск вектора С, при котором функция (11.22) достигает своего % минимального значения, вектор С — коэффициенты функции fi. C=sqp (C, @f_mnk) % Вычисление ординат точек графика второй функции g(x). Y2=A(1)+A(2)*X1+A(3)*X1.^2+A(4)*X1.^3+A(5)*X1.^5; % Вычисление ординат точек графика третьей функции fi(x). Y3=C(1)+C(2)*X1+C(3)*X1.^3+C(4)*X1.^5; % Вычисление значений первой функции f(x) в заданных точках. yr1=polyval(B, x); % Вычисление значений второй функции g(x) в заданных точках. yr2=A(1)+A(2)*x+A(3)*x.^2+A(4)*x.^3+A(5)*x.^5; % Вычисление значений третьей функции fi(x) в заданных точках. yr3=C(1)+C(2)*x+C(3)*x.^3+C(4)*x.^5; % Вычисление индекса корреляции для первой функции f(x). R1=sqrt(1-sum((y-yr1).^2)/sum((y-mean(y)).^2)) % Вычисление индекса корреляции для второй функции g(x). R2=sqrt(1-sum((y-yr2).^2)/sum((y-mean(y)).^2)) % Вычисление индекса корреляции для третьей функции fi(x). R3=sqrt(1-sum((y-yr3).^2)/sum((y-mean(y)).^2)) % Сравнивая значения трёх индексов корреляции, выбираем наилучшую % функцию и с её помощью вычисляем ожидаемое значение в точках 1, 2.5, 4.8. if R1>R2 & R1>R3 yz=polyval(B, z) "R1="; R1 endif if R2>R1 & R2>R3 yz=C2(1)+C2(2)*z+C2(3)*z.^2+C2(4)*z.^3+C2(5)*z.^5 "R2="; R2 endif if R3>R1 & R3>R2 yz=C(1)+C(2)*z+C(3)*z.^3+C(4)*z.^5 "R3="; R3 endif % Построение графика. plot(x, y, "*r;experiment;",X1, Y1, ’-b;f(x);’,X1, Y2, ’dr;g(x);’,X1 , Y3, ’ok;fi(x);’, z, yz, ’sb;f(z);’); grid(); % Результаты работы программы. z = 1.0000 2.5000 4.8000 B = 0.083039 -0.567892 0.906779 1.609432 -1.115925 -1.355075 GGL = 1.3000e+01 2.8600e+01 1.5210e+02 7.2701e+02 1.2793e+05 2.8600e+01 1.5210e+02 7.2701e+02 3.9868e+03 7.5030e+05 1.5210e+02 7.2701e+02 3.9868e+03 2.2183e+04 4.4706e+06 7.2701e+02 3.9868e+03 2.2183e+04 1.2793e+05 2.6938e+07 2.2183e+04 1.2793e+05 7.5030e+05 4.4706e+06 1.6383e+08 A = 9.4262e+00 -3.6516e+00 -5.7767e+00 1.7888e+00 -5.8179e-05 C = -1.030345 5.080391 -0.609721 0.033534 R1 = 0.99690 R2 = 0.98136 R3 = 0.99573 yz = -0.43964 6.008544 0.77972Листинг 11.4. Решение к примеру 11.3
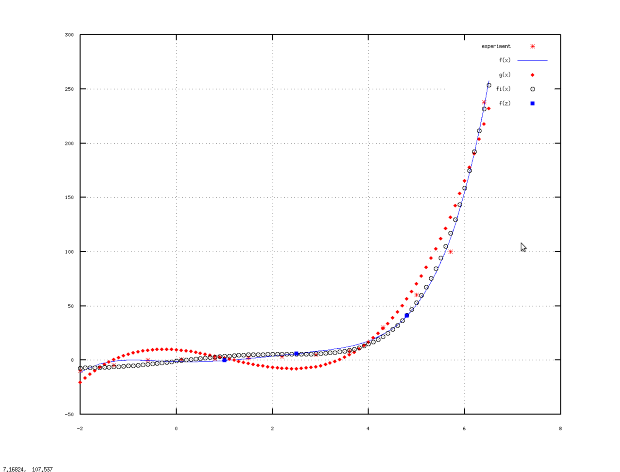
На рисунке 11.4 представлено графическое решение задачи.
Рассмотренная задача демонстрирует основные приёмы подбора зависимости методом наименьших квадратов. Авторы рекомендует внимательно рассмотреть её для понимания методов решения подобных задач в Octave.
В заключении авторы позволят несколько советов по решению задачи аппроксимации.
- Подбор каждой зависимости по экспериментальным данным — довольно сложная математическая задача, поэтому следует аккуратно выбирать вид зависимости, наиболее точно описывающей экспериментальные точки.
- Необходимо сформировать реальную систему уравнений исходя из соотношений (11.1)–(11.3). Следует помнить, что проще и точнее решать систему линейных алгебраических уравнений, чем систему нелинейных уравнений. Поэтому, может быть, следует преобразовать исходную функцию (прологарифмировать, сделать замену и т. д.) и только после этого составлять систему уравнений.
- При том, что функция
 — довольно мощная, лучше использовать методы и функции решения систем линейных алгебраических уравнений, функцию
— довольно мощная, лучше использовать методы и функции решения систем линейных алгебраических уравнений, функцию  , чем функцию
, чем функцию  . Этот совет связан с тем, что функция
. Этот совет связан с тем, что функция  — приближённые итерационные алгоритмы, поэтому получаемый результат иногда может быть менее точен, чем при точных методах решения систем линейных алгебраических уравнений. Но, иногда, именно функция
— приближённые итерационные алгоритмы, поэтому получаемый результат иногда может быть менее точен, чем при точных методах решения систем линейных алгебраических уравнений. Но, иногда, именно функция  — единственный метод решения задачи.
— единственный метод решения задачи. - Для оценки корректности подобранной зависимости следует использовать коэффициент корреляции, критерий Стьюдента (для линейной зависимости) и индекс корреляции и суммарную квадратичную ошибку (для нелинейных зависимостей).