НОУ ИНТУИТ | Введение в Octave. Лекция 11: Обработка результатов эксперимента. Метод наименьших квадратов

Учитесь и получайте официальные документы БЕСПЛАТНО. Вы можете поддержать наш проект.

Регистрация Вход

Твой путь к знаниям!

Компания ALT Linux

Опубликован: 12.03.2015 | Доступ: свободный | Студентов: 583 / 65 | Длительность: 20:55:00

Темы: Математика, Программное обеспечение, Физика

Специальности: Математик, Преподаватель, Физик

|

Вам нравится? Нравится 15 студентам

| Поделиться |

Поддержать курс

| Скачать электронную книгу

11.2.3 Подбор коэффициентов функции

$Y=ax^be^{cx}$

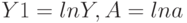Параметры и входят в зависимость $Y=ax^be^{cx}$ нелинейным образом. Чтобы избавиться от нелинейности предварительно прологарифмируем^{1Можно и не проводить предварительное логарифмирование выражения , однако в этом случаем получаемая система уравнений будет нелинейной, которую решать сложнее.} выражение $Y=ax^be^{cx}:\ln Y=\ln a+b\ln x+cx$ . 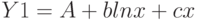Сделаем замену Y1 = lnY, A = ln a , после этого функция примет вид: Y1 = A + blnx + cx .

Составим функцию 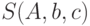S(A, b, c) по формуле (11.1):

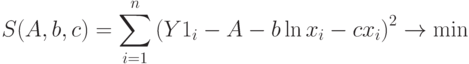$S(A,b,c)=\sum_{i=1}^n\left(Y1_i-A-b\ln x_i-cx_i\right)^2\to\min$

( 11.15)

После дифференцирования получим систему трёх линейных алгебраических уравнений для определения коэффициентов 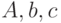A, b, c .

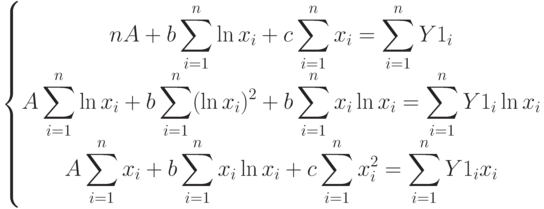$\left\{ \begin{matrix} \displaystyle nA+b\sum_{i=1}^n\ln x_i+c\sum_{i=1}^nx_i=\sum_{i=1}^nY1_i\\ \displaystyle A\sum_{i=1}^n\ln x_i+b\sum_{i=1}^n(\ln x_i)^2+b\sum_{i=1}^nx_i\ln x_i=\sum_{i=1}^nY1_i\ln x_i\\ \displaystyle A\sum_{i=1}^nx_i+b\sum_{i=1}^nx_i\ln x_i+c\sum_{i=1}^nx_i^2=\sum_{i=1}^nY1_ix_i \end{matrix} \right.$

( 11.16)

После решения системы (11.16) необходимо вычислить значение коэффициента a по формуле 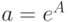a=e^A .

11.2.4 Функции, приводимые к линейной

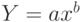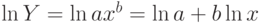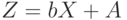Для вычисления параметров функции Y = ax^b необходимо предварительно её прологарифмировать $\ln Y=\ln ax^b=\ln a+b\ln x$ . После чего замена Z = lnY, X = lnx, A = lna приводит заданную функцию к линейному виду Z = bX + A , где коэффициенты и вычисляются по формулам (11.6) и, соответственно, a=e^A .

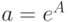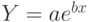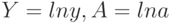Аналогично можно подобрать параметры функции вида $Y = ae^{bx}$ . Прологарифмируем заданную функцию $\ln y=\ln a+bx\ln e,\ln y=\ln a+bx$ . Проведём замену Y = lny, A = lna и получим линейную зависимость 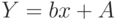Y = bx + A . По формулам (11.6) найдём и , а затем вычислим a=e^A .

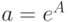Рассмотрим ещё ряд зависимостей, которые сводятся к линейной.

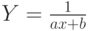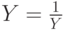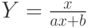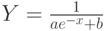Для подбора параметров функции $Y=\frac{1}{ax+b}$ сделаем замену $Y=\frac{1}{Y}$ . В результате получим линейную зависимость Z = ax + b. Функция $Y=\frac{x}{ax+b}$ заменами $Z=\frac{1}{Y}$ , $X=\frac{1}{x}$ сводится к линейной Z = a + bX. Для определения коэффициентов функциональной зависимости $Y=\frac{1}{ae^{-x}+b}$ необходимо сделать следующие замены 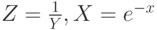$Z=\frac{1}{Y},X=e^{-x}$ . В результате также получим линейную функцию Z = aX + b.

Аналогичными приёмами (логарифмированием, заменами и т. п.) можно многие подбираемые зависимости преобразовать к такому виду, что получаемая при решении задачи оптимизации система (11.2) была системой линейных алгебраических уравнений. При использовании Octave можно напрямую решать задачу подбора параметров, как задачу оптимизации (11.1) с использованием функции sqp.

После нахождения параметров зависимости 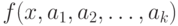$f(x,a_{1},a_{2},\dots, a_{k})$ возникает вопрос насколько адекватно описывает подобранная зависимость экспериментальные данные. Чем ближе величина

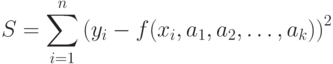$S=\sum_{i=1}^n\left(y_i-f(x_i,a_1,a_2,\dots,a_k)\right)^2$

( 11.17)

называемая суммарной квадратичной ошибкой, к нулю, тем точнее подобранная кривая описывает экспериментальные данные.

Дальше >>

Авторизоваться

Введение в Octave

Обработка результатов эксперимента. Метод наименьших квадратов

11.2.3 Подбор коэффициентов функции

11.2.4 Функции, приводимые к линейной

Вопросы и ответы