|
Возможна ли разработка приложения на Octave с GUI? |
Решение оптимизационных задач
Изучение оптимизационных задач начнём с обычных задач поиска минимума (максимума) функции одной или нескольких переменных.
10.1 Поиск экстремума функции
Для решения классических оптимизационных задач с ограничениями в Octave можно воспользоваться следующей функцией ![[x, obj, info, iter] = sqp(x_0, phi, g, h, lb, ub, maxiter, tolerance)](/sites/default/files/tex_cache/a4a647735091625565821c483eed8c4c.png) , которая предназначена для решения следующей оптимизационной задачи.
, которая предназначена для решения следующей оптимизационной задачи.
Найти минимум функции 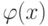 при следующих ограничениях
при следующих ограничениях 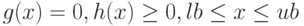 . Функция
. Функция  при решении задачи оптимизации использует метод квадратичного программирования.
при решении задачи оптимизации использует метод квадратичного программирования.
Аргументами функции  являются:
являются:
-
 — начальное приближение значения
— начальное приближение значения  ,
, -
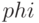 — оптимизируемая функция
— оптимизируемая функция 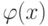 ,
, -
 и
и  — функции ограничений
— функции ограничений 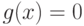 и
и 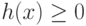 ,
, -
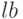 и
и 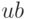 — верхняя и нижняя границы ограничения
— верхняя и нижняя границы ограничения 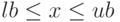 ,
, -
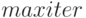 — максимальное количество итераций, используемое при решении оптимизационной задачи, по умолчанию эта величина равна 100,
— максимальное количество итераций, используемое при решении оптимизационной задачи, по умолчанию эта величина равна 100, -
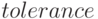 — точность
— точность  , определяющая окончание вычислений, вычисления прекращаются при достижении точности
, определяющая окончание вычислений, вычисления прекращаются при достижении точности  .
.
Функция  возвращает следующие значения:
возвращает следующие значения:
-
 — точка, в которой функция, достигает своего минимального значения,
— точка, в которой функция, достигает своего минимального значения, -
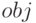 — минимальное значение функции,
— минимальное значение функции, -
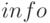 — параметр, характеризующий корректность решения оптимизационной задачи, (если функция sqp возвращает значение info = 101, то задача решена правильно),
— параметр, характеризующий корректность решения оптимизационной задачи, (если функция sqp возвращает значение info = 101, то задача решена правильно), -
 — реальное количество итераций при решении задачи.
— реальное количество итераций при решении задачи.
Рассмотрим несколько примеров использования функции  при решении задач поиска экстремума функции одной переменной без ограничений.
при решении задач поиска экстремума функции одной переменной без ограничений.
Пример 10.1. Найти минимум функции 
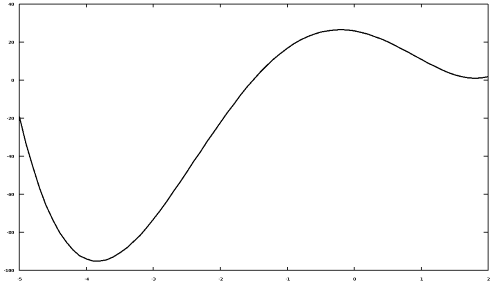
При решении задачи оптимизации с помощью функции sqp необходимо иметь точку начального приближения. Построим график функции 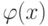 (см. рис. 10.1). Из графика видно, что функция имеет минимум в окрестности точки
(см. рис. 10.1). Из графика видно, что функция имеет минимум в окрестности точки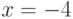 . В качестве точки начального приближения выберем
. В качестве точки начального приближения выберем 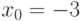 . Решение задачи представлено в листинге 10.1.
. Решение задачи представлено в листинге 10.1.
function obj = phi(x) obj = x^4+3*x^3-13*x^2-6*x+26; endfunction [x, obj, info, iter]= sqp(-3, @phi) % Результаты решения x =-3.8407 obj =-95.089 info = 101 iter = 5Листинг 10.1. Поиск минимума функции (пример 10.1)
Минимум функции 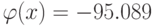 достигается в точке
достигается в точке 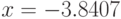 , количество итераций равно 5, параметр
, количество итераций равно 5, параметр 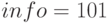 свидетельствует о корректном решении задачи поиска минимума
свидетельствует о корректном решении задачи поиска минимума 
Рассмотрим пример поиска минимума функции нескольких переменных.