|
Возможна ли разработка приложения на Octave с GUI? |
Решение обыкновенных дифференциальных уравнений и систем
function[x, t, j]=kut_merson(a, b, n, eps, x0) % Функция решения задачи Коши x'(t) = g(t, x)x(a) = x0 методом % Кутта-Мерсона на интервале интегрирования [a, b] c точностью eps, % n — количество отрезков, на которые вначале разбивается интервал [a, b]. h=(b-a)/n; % Вычисление шага h. x(1)=x0; t(1)=a; i=2; while(t(i-1)+h)<=b R=3*eps; while R>eps % Расчёт коэффициентов K1, K2, K3, K4, K5. K1=g(t(i-1), x(i-1)); K2=g(t(i-1)+h/3, x(i-1)+h/3*K1); K3=g(t(i-1)+h/3, x(i-1)+h/6*K1+h/6*K2); K4=g(t(i-1)+h/2, x(i-1)+h/8*K1+3*h/8*K2); K5=g(t(i-1)+h, x(i-1)+h/2*K1-3*h/2*K3+2*h*K4); % Вычисление сравниваемых значений x(i+1) X1=x(i-1)+h/2*(K1-3*K3+4*K4); X2=x(i-1)+h/6*(K1+4*K4+K5); % Вычисление оценочного коэффициента R. R=0.2*abs(X1-X2); % Сравнение оценочного коэффициента R с точностью eps. if R>eps h=h/2; else % Если оценочный коэффициент R меньше точности eps, % то происходит формирование очередной найденной точки и % переход к следующему этапу по i. t(i)=t(i-1)+h; x(i)=X2; i=i+1; % Если оценочный коэффициент R меньше eps/64, % то можно попробовать увеличить шаг. if R<= eps/64 if (t(i-1)+2*h)<=b h=2*h; end end end end end % В переменной j возвращается количество элементов в массивах x и t j=i-1 endЛистинг 9.4. Функция решения задачи Коши методом Кутта-Мерсона.
function[x, t]=adams(a, b, n, x0) % Функция решения задачи Коши x'(t) = g(t, x) x(a) = x0 методом Адамса % n — количество отрезков, на которые разбивается интервал [a, b]. h=(b-a)/n; % Вычисление шага h x(1)=x0; for i=1:n+1 % Формирование системы равноотстоящих узлов ti. t(i)=a+(i-1)*h; end % Вычисление значений функции в трёх узловых точках по формуле(9.16) for i =2:4 K1=g(t(i-1), x(i-1)); K2=g(t(i-1)+h/2, x(i-1)+h/2*K1); K3=g(t(i-1)+h/2, x(i-1)+h/2*K2); K4=g(t(i-1)+h, x(i-1)+h*K3); % Расчёт приращения delt delt=h/6*(K1+2*K2+2*K3+K4); x(i)=x(i-1)+delt; end for i =4:n % Вычисление значений в остальных точках методом Адамса % Вычисление прогноза xp=x(i)+h/24*(-9*g(t(i-3), x(i-3))+37*g(t(i-2), x(i-2)) -59*g(t(i-1), x(i-1))+55*g(t(i), x(i))); % Вычисление корректора x(i+1)=x(i)+h/24*(g(t(i-2), x(i-2))-5*g(t(i-1), x(i-1)) +19*g(t(i), x(i))+9*g(t(i+1), xp)); end endЛистинг 9.5. Функция решения задачи Коши методом Адамса.
function[x, t]= miln(a, b, n, x0) % Функция решения задачи Коши x'(t) = g(t, x) x(a) = x0 методом Милна % n — количество отрезков, на которые разбивается интервал [a, b]. h=(b-a)/n; % Вычисление шага h x(1)=x0; xp(1)=x(1); for i =1:n+1 % Формирование системы равноотстоящих узлов ti t(i)=a+(i-1)*h; end % Вычисление значений функции в трёх узловых точках по формуле (9.16) for i =2:4 K1=g(t(i-1), x(i-1)); K2=g(t(i-1)+h/2, x(i-1)+h/2*K1); K3=g(t(i-1)+h/2, x(i-1)+h/2*K2); K4=g(t(i-1)+h, x(i-1)+h*K3); % Расчёт приращения delt delt=h/6*(K1+2*K2+2*K3+K4); x(i)=x(i-1)+delt; xp(i)=x(i); end for i =4:n % Вычисление значений в остальных точках методом Адамса % Вычисление прогноза xp(i+1)=x(i-3)+4*h/3*(2*g(t(i-2), x(i-2))-g(t(i-1), x(i -1))+g(t(i), x(i))); % Вычисление управляющего параметра m=xp(i+1)+28/29*(x(i)-xp(i)); % Вычисление корректора. x(i+1)=x(i-1)+h/3*(g(t(i-1), x(i-1))+4*g(t(i), x(i))+g(t (i+1), m)); end endЛистинг 9.6. Функция решения задачи Коши методом Милна
Написать функцию модифицированного метода Милна авторы предоставляют читателю.
Рассмотрим использование приведённых выше функций на примере решения следующей задачи Коши.
Пример 9.1. Решить задачу Коши
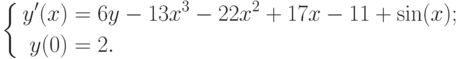
Известно точное решение задачи 9.1:
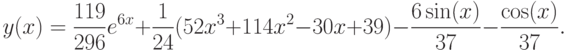
В листинге 9.7 представлено решение уравнения методами:
- модифицированным методом Эйлера;
- Рунге-Кутта;
- Кутта-Мерсона;
- Адамса;
- Милна.
% Точное решение function q= fi(x) q=119/296*exp(6*x)+1/24*(52*x.^3+114*x.^2-30*x+39)-6*sin(x )/37-cos(x)/37; end % Правая часть дифференциального уравнения. function y=g(t, x) y=6-x-13*t^3-22*t^2+17*t-11+sin(t); end % Функция решения задачи Коши модифицированным методом Эйлера. function[x, t]= eiler_m(a, b, n, x0) h=(b-a)/n; x(1)=x0; for i =1:n+1 t(i)=a+(i-1)*h; end for i =2:n+1 tp=t(i-1)+h/2; xp=x(i-1)+h/2*g(t(i-1), x(i-1)); x(i)=x(i-1)+h*g(tp, xp); end end % Функция решения задачи Коши методом Рунге-Кутта. function[x, t]=runge_kut(a, b, n, x0) h=(b-a)/n; x(1)=x0; for i =1:n+1 t(i)=a+(i-1)*h; end for i =2:n+1 K1=g(t(i-1), x(i-1)); K2=g(t(i-1)+h/2, x(i-1)+h/2*K1); K3=g(t(i-1)+h/2, x(i-1)+h/2*K2); K4=g(t(i-1)+h, x(i-1)+h*K3); delt=h/6*(K1+2*K2+2*K3+K4); x(i)=x(i-1)+delt; end end % Функция решения задачи Коши методом Кутта-Мерсона. function[x, t,j ]=kut_merson(a, b, n, eps, x0) h=(b-a)/n; x(1)=x0; t(1)=a; i=2; while(t(i-1)+h)<=b R=3*eps; while R>eps K1=g(t(i-1), x(i-1)); K2=g(t(i-1)+h/3, x(i-1)+h/3*K1); K3=g(t(i-1)+h/3, x(i-1)+h/6*K1+h/6*K2); K4=g(t(i-1)+h/2, x(i-1)+h/8*K1+3*h/8*K2); K5=g(t(i-1)+h, x(i-1)+h/2*K1-3*h/2*K3+2*h*K4); X1=x(i-1)+h/2*(K1-3*K3+4*K4); X2=x(i-1)+h/6*(K1+4*K4+K5); R=0.2*abs(X1-X2); if R>eps h=h/2; else t(i)=t(i-1)+h; x(i)=X2; i=i+1; if R<= eps/64 if (t(i-1)+2*h)<=b h=2*h; end end end end end j=i-1 end % Функция решения задачи Коши методом Милна. function[x, t]= miln(a, b, n, x0) h=(b-a)/n; x(1)=x0; xp(1)=x(1); for i =1:n+1 t(i)=a+(i-1)*h; end for i =2:4 K1=g(t(i-1), x(i-1)); K2=g(t(i-1)+h/2, x(i-1)+h/2*K1); K3=g(t(i-1)+h/2, x(i-1)+h/2*K2); K4=g(t(i-1)+h, x(i-1)+h*K3); delt=h/6*(K1+2*K2+2*K3+K4); x(i)=x(i-1)+delt; xp(i)=x(i); end for i =4:n xp(i+1)=x(i-3)+4*h/3*(2-g(t(i-2), x(i-2))-g(t(i-1), x(i -1))+g(t(i), x(i))); m=xp(i+1)+28/29*(x(i)-xp(i)); x(i+1)=x(i-1)+h/3*(g(t(i-1), x(i-1))+4*g(t(i), x(i))+g(t (i+1),m)); end end % Функция решения задачи Коши методом Адамса. function[x, t]=adams(a, b, n, x0) h=(b-a)/n; x(1)=x0; for i =1:n+1 t(i)=a+(i-1)*h; end for i =2:4 K1=g(t(i-1), x(i-1)); K2=g(t(i-1)+h/2, x(i-1)+h/2*K1); K3=g(t(i-1)+h/2, x(i-1)+h/2*K2); K4=g(t(i-1)+h, x(i-1)+h* K3); delt=h/6*(K1+2*K2+2*K3+K4); x(i)=x(i-1)+delt; end for i =4:n xp=x (i)+h/24*(-9*g(t(i-3), x(i-3))+37*g(t(i-2), x(i-2)) -59*g(t(i-1), x(i-1)) +55*g(t(i), x(i))); x(i+1)=x(i)+h/24*(g(t(i-2), x(i-2))-5*g(t(i-1), x(i-1)) +19*g(t(i), x(i))+9*g(t(i+1), xp)); end end % Решение дифференциального уравнения модифицированным методом Эйлера. [YE_M,XE_M]= eiler_m(0, 1, 10, 2); % Решение дифференциального уравнения методом Рунге-Кутта. [YR,XR]= runge_kut(0, 1, 10, 2); % Решение дифференциального уравнения методом Кутта-Мерсона. [YKM,XKM,KM]=kut_merson(0, 1, 5, 0.001, 2); % Решение дифференциального уравнения методом Адамса. [YA,XA]=adams(0, 1, 10, 2); % Решение дифференциального уравнения методом Милна. [YM,XM]= miln(0, 1, 10, 2); % Точное решение. x1 = 0:0.05:1; y1= fi(x1); % Построение графиков. plot(x1, y1, ’-g;exact solution;’,XE_M,YE_M, ’*b;eiler;’,XR,YR, ’ ob;runge-kutt;’,XA,YA, ’^b;adams;’,XM,YM, ’>b;miln;’); figure(); plot(x1, y1, ’-g;exact solution;’,XKM,YKM, ’<b;kut -merson;’); grid on;Листинг 9.7. Различные методы решения задачи Коши (пример 9.1.)
увеличить изображение
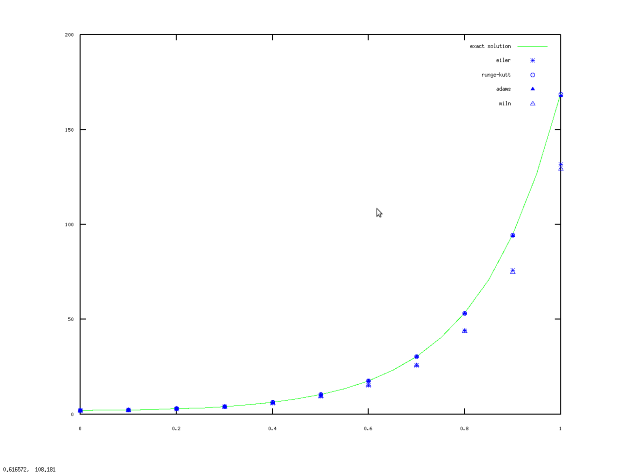
Рис. 9.3. Графики решения модифицированным методом Эйлера, методами Рунге-Кутта, Адамса, Милна и точного решения
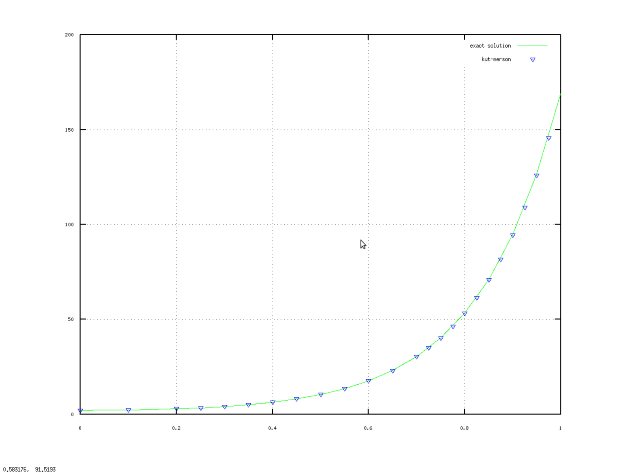
На рис. 9.3–9.4 приведены графики решения задачи модифицированным методом Эйлера, методами Рунге-Кутта, Кутта-Мерсона, Адамса, Милна и точного решения. При обращении к функции  в качестве
в качестве  передавалось число 5.
передавалось число 5.
Функция выбирала оптимальный шаг на каждом из отрезков. Как видно из рисунка, шаг то увеличивается, то уменьшается. При решении уравнения методом Кутта-Мерсона невозможно гарантировать вычисление значения в заданных точках интервала. Однако после получения решения методом Кутта-Мерсона значение в любой точки можно вычислить, интерполируя полученную зависимость.
При решении данной задачи наиболее точными оказались методы Адамса, Рунге-Кутта и Кутта-Мерсона.