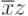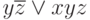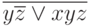Основные понятия алгебры логики. Функции алгебры логики. Основные логические эквивалентности
Вычисление логических функций
Логическая функция может быть представлена несколькими способами, каждый из которых наиболее эффективен для той или иной области применения. Рассмотрим ситуацию, когда логическая функция представлена в виде суперпозиции элементарных логических функций, а для последующей ее обработки, например, для построения некоторого схемотехнического устройства, необходимо иметь представление функции в виде таблицы истинности.
Пример 1.1. Представить таблицу истинности следующей логической функции:

Сначала примем во внимание приоритеты логических операций.
Логические операции выполняются в следующем порядке:
- самый высокий приоритетимеет операция инверсия (НЕ) отдельных переменных;
- операция конъюнкция (И) имеет приоритет второго уровня;
- остальные операции не имеют приоритета и выполняются по очереди слева направо.
Естественно, что порядок выполнения операций можно изменять посредством применения скобок.
Проведем в соответствии с этим порядком вычисление указанной выше функции.