Основные понятия алгебры логики. Функции алгебры логики. Основные логические эквивалентности

Эквивалентность ФАЛ.

Логические функции являются эквивалентными, если их значения совпадают для всех допустимых наборов аргументов. Так как аргументами ФАЛ являются логические переменные, которые могут принимать только два значения ("Истина" либо "Ложь", которые, как было сказано выше, обычно обозначаются "1" и "0"), то доказательство эквивалентности логических функций сводится к сравнению их таблиц истинности.

Конъюнкция

Основные свойства:

0 & 0 = 0

0 & 1 = 0

1 & 1 = 1

0 & x = 0

1 & x = x

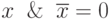
x & x &...& x = x

x & y = y & x

x & y & z = (x & y) & z = x & (y & z)

Для более легкого запоминания этой функции следует придерживаться правила: функция конъюнкции ложна, если ложен хотя бы один из ее операндов. Это правило действует для функции, содержащей произвольное число операндов. Если обозначать значение "истина" как "1", а значение "ложь" как "0", то эта функция будет похожа на математическую функцию умножения. Поэтому ее зачастую называют функцией логического умножения.

Отметим, что для конъюнкции, так же как и для следующей рассматриваемой функции – дизъюнкции – действуют ассоциативный (сочетательный) и коммуникативный (переместительный) законы.

В то же время для некоторых других логических функций тот или иной закон не действует. Некоторые из примеров таких функций мы рассмотрим ниже.

Покажем, например, что .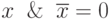

Как уже говорилось ранее, основным доказательством эквивалентности двух функций служит тот факт, что они имеют одинаковые таблицы истинности на всех наборах аргументов.

Но в данном случае можно поступить проще. Так как функция зависит только от одной логической переменной, которая может принимать только значения "0" или "1" и, то в рассматриваемом выражении один из операндов всегда будет равен "0" (при x =0 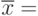"1", а при x = 1 ).Учитывая, что 0 & x = 0, получаем, что рассматриваемые функции эквивалентны.