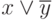Основные понятия алгебры логики. Функции алгебры логики. Основные логические эквивалентности
Штрих Шеффера (И-НЕ)
Штрих Шеффера (И-НЕ)1Шеффер, Генри Морисс (1882-1964) –американский учёный украинского происхождения
Основные свойства:
0/0 = 1
0/1 = 1
1/1 = 0
0/x = 1
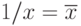
x/y = y/x
x/(y/z) ≠ (x/y)/z
Иногда ФАЛ "Штрих Шеффера" называют операцией "И-НЕ". И действительно, для двух переменных это так. Но если мы будем использовать большее количество переменных, то соотношение нарушается.
И, в то же время, для трёх и более переменных таблица истинности ФАЛ "Штрих Шеффера" совпадает с таблицей истинности функции "И-НЕ". Поэтому иногда в литературе можно встретить мнение о том, что операция "Штрих Шеффера" применима лишь для двух переменных. В остальных случаях следует говорить об операции "И-НЕ", при которой сначала выполняется конъюнкция всех переменных, от которых зависит ФАЛ, а затем проводится операция "НЕ" над полученным результатом.
Таким образом, для любого числа переменных функция "Штрих Шеффер" истинна, если хотя бы один из используемых аргументов ложен.
Покажем, что логическая функция x/(y/z) не эквивалентна ФАЛ (x/y)/z, то есть, что функции штрих Шеффера не действует сочетательный закон. Для этого построим таблицу истинности для первой и второй ФАЛ.
| x | y | z | x/y | (x/y)/z |
|---|---|---|---|---|
| 0 | 0 | 0 | 1 | 1 |
| 0 | 0 | 1 | 1 | 0 |
| 0 | 1 | 0 | 1 | 1 |
| 0 | 1 | 1 | 1 | 0 |
| 1 | 0 | 0 | 1 | 1 |
| 1 | 0 | 1 | 1 | 0 |
| 1 | 1 | 0 | 0 | 1 |
| 1 | 1 | 1 | 0 | 1 |
| x | y | z | y/z | x/(y/z) |
|---|---|---|---|---|
| 0 | 0 | 0 | 1 | 1 |
| 0 | 0 | 1 | 1 | 1 |
| 0 | 1 | 0 | 1 | 1 |
| 0 | 1 | 1 | 0 | 1 |
| 1 | 0 | 0 | 1 | 0 |
| 1 | 0 | 1 | 1 | 0 |
| 1 | 1 | 0 | 1 | 0 |
| 1 | 1 | 1 | 0 | 1 |
Как мы видим, таблицы истинности для первой и второй функций не совпадают, то есть эти функции не эквивалентны.
Также приведём таблицу истинности ФАЛ "И-НЕ" для трех переменных.
| x | y | z | x&y&z | "И-НЕ"(x,y,z) |
|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 1 |
| 0 | 0 | 1 | 0 | 1 |
| 0 | 1 | 0 | 0 | 1 |
| 0 | 1 | 1 | 0 | 1 |
| 1 | 0 | 0 | 0 | 1 |
| 1 | 0 | 1 | 0 | 1 |
| 1 | 1 | 0 | 0 | 1 |
| 1 | 1 | 1 | 1 | 0 |
Стрелка Пирса (функция Вэбба) (ИЛИ-НЕ)2Чарльз Пирс – американский математик (1839—1914)
В некоторых источниках можно встретить разночтения в названии и обозначении этой ФАЛ. Иногда ее называют элементом Вэбба, иногда обозначают вертикально вверх направленной стрелкой. Мы в дальнейшем эту логическую функцию будем называть стрелкой Пирса и обозначать стрелкой, направленной вертикально вниз.
Свойства
0↓0 = 1
0↓1 = 0
1↓1 = 0
0↓x =x
1↓x = 0
x↓y=y↓x
x↓(y↓z) ≠ (x↓y)↓z
В отношении этой функции можно сказать примерно то же самое, что было сказано по поводу ФАЛ "Штрих Шеффера": для функции от двух переменных она эквивалентна функции "ИЛИ-НЕ". В то же время ассоциативный закон для нее не выполняется.
Прервем на немного рассмотрение отдельных функций и расскажем о правилах, которые зачастую помогаю существенно упростить то или иное логическое выражение.
Правила де Моргана.3Огастес (Август) де Мо́рган – шотладский математик и логик (1806-1871)Применительно к рассмотренным функциям, данные правила позволяют выполнить переход от одной формы представления логической функции к другой:

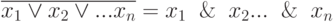
x1 & x2 & ... & xn = x1 v x2 v ... xn
x1 v x2 v ... xn = x1 & x2 & ... & xn
Или, описывая эти преобразования словесно, можно сказать, что "отрицание конъюнкций есть дизъюнкция отрицаний" и, в свою очередь, "отрицание дизъюнкций есть конъюнкция отрицаний".
Этими правилами мы будем в дальнейшем часто пользоваться.
При минимизации логических функций используются следующие эквивалентные преобразования.
Операция склеивания:
 |
( 1.1) |
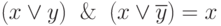 |
( 1.2) |
Операция неполного склеивания:
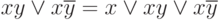
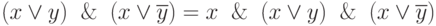
Операция поглощения:
x v xy = x
x v xy = x
Казалось бы, что операция неполного склеивания не имеет отношение к минимизации, так как получаемое выражение больше исходного. Однако, эта операция играет очень важную роль при минимизации, что бы позднее покажем.
А пока покажем эквивалентность, например, одной из операций склеивания:
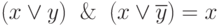
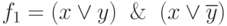
Ее таблица истинности имеет вид:
Это соответствует таблице истинности ƒ2(x,y) = x.
А теперь рассмотрим еще одну функцию, играющую важную роль в арифметических и логических основах ЭВМ.