Приведенная ценность финансовой ренты
7.6 Процентная ставка финансовой ренты
При финансовых вычислениях может возникнуть необходимость по известному коэффициенту наращения 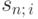 или по известному коэффициенту приведёния
или по известному коэффициенту приведёния 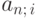 найти значение процентной ставки i при фиксированном числе членов ренты n. Опишем одну из возможных ситуаций, в которой возникает такая необходимость. Фирме требуется накопить сумму s к определённому сроку, делая через равные промежутки времени n равных вкладов, размером R каждый. Какой минимальный процент на вложенные деньги надо получать для этого в банке? В этом случае, зная значения s, R, n, можно найти значение
найти значение процентной ставки i при фиксированном числе членов ренты n. Опишем одну из возможных ситуаций, в которой возникает такая необходимость. Фирме требуется накопить сумму s к определённому сроку, делая через равные промежутки времени n равных вкладов, размером R каждый. Какой минимальный процент на вложенные деньги надо получать для этого в банке? В этом случае, зная значения s, R, n, можно найти значение 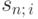 , а затем по этому значению вычислить процентную ставку i.
, а затем по этому значению вычислить процентную ставку i.
Возможна другая ситуация. Вкладчик желает положить сумму s на счет в банке, чтобы после этого иметь возможность n раз снять со своего счета через равные промежутки времени сумму, равную R. Вкладчику интересно узнать, сколько процентов при этом должен платить банк на вложенные деньги. В этом случае по известным значениям s, R и n можно найти значение 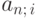 по формуле (7.2), а затем по этому значению вычислить ставку i.
по формуле (7.2), а затем по этому значению вычислить ставку i.
В описанных ситуациях надо решить относительно i уравнение n-й степени при заданных значениях q, n, 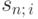 или
или 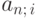 :
:
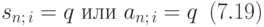
Для решения таких уравнений типа уравнения (7.19) существуют методы нахождения приближённых значений корней с любой степенью точности. Опишем один из этих методов: метод линейной интерполяции.
Этот метод использует тот факт, что если непрерывная функция f(x) является на промежутке [ ] монотонной (возрастающей или убывающей) и принимает на концах этого промежутка разные знаки, то в некоторой внутренней точке этого промежутка функция f(x) равна нулю, и эта точка (корень функции) единственная на данном промежутке. Приближённое значение корня функции на этом промежутке вычисляется по следующей формуле:
] монотонной (возрастающей или убывающей) и принимает на концах этого промежутка разные знаки, то в некоторой внутренней точке этого промежутка функция f(x) равна нулю, и эта точка (корень функции) единственная на данном промежутке. Приближённое значение корня функции на этом промежутке вычисляется по следующей формуле:
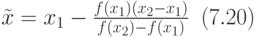
Мы применим этот метод при решении следующего примера. Необходимые вычисления могут быть легко проведены с помощью финансового калькулятора или в Excel. В п. 7.7 будет рассказано, как решать подобные задачи с помощью специальных средств Excel.
Пример 68 Для возвращения долга необходимо накопить за 10 лет 2 млн руб. Ежегодно должник может вносить в банк для этой цели 150 тыс. руб. Под какую ставку сложных процентов необходимо вкладывать эти деньги, чтобы накопить требуемую сумму в указанный срок?
Решение. По условию примера необходимо за 10 лет получить наращенную сумму S=2 млн руб. Применяя формулу из лекции 6, находим коэффициент наращения:

Следовательно, надо решить относительно i уравнение (7.19). Оно имеет вид:
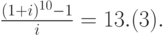
Это уравнение десятой степени. Запишем это уравнение в виде
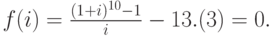
Подбором находим два значения i, при которых функция f(i) имеет разные знаки: i=5% и i=10%. Действительно, при этих значениях i мы имеем:

На промежутке [0.05; 0.10] функция f(i) меняет знак и монотонно возрастает. Находим приближённое значение i по формуле (7.20), заменив переменную x переменной i. В нашем примере имеем в качестве начальных данных:
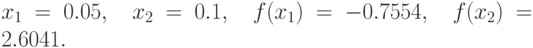
Приближённое значение корня уравнения 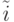 , согласно формуле (7.20), равно:
, согласно формуле (7.20), равно:
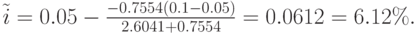
Вычислим значение f(0.0612):
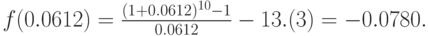
Это значение близко к 0, поэтому приближённое значение корня уравнения i=6.12% можно принять в качестве решения поставленной задачи.
Если точность найденного значения i будет признана недостаточной, то следует вновь применить формулу (7.20) на промежутке [6.12%; 10%], так как функция на концах этого промежутка имеет разные знаки:
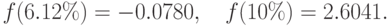
Повторяя эту процедуру, можно найти значение i с любой степенью точности.
