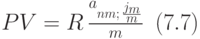Опубликован: 24.09.2017 | Доступ: свободный | Студентов: 1241 / 371 | Длительность: 12:18:00
Тема: Менеджмент
Специальности: Менеджер, Руководитель, Экономист
Лекция 7:
Приведенная ценность финансовой ренты
7.3.2 Ренты с начислением процентов m раз в год
Годовая рента
Используя формулы из лекций 3 и 6, находим значение приведённой ценности этой ренты:
![PV = S\left(1+{j_{m}\over m}\right)^{-nm}=
R\,\frac{\left(1+{j_{m}\over m}\right)^{nm}-1}{\left(1+{j_{m}\over
m}\right)^{m}-1}\left(1+{j_{m}\over m}\right)^{-nm}=\\[8pt]
= R\frac{1-\left(1+{j_{m}\over m}\right)^{-nm}}{\left(1+{j_{m}\over
m}\right)^{m}-1}=R\,\frac{\displaystyle\frac{1-\left(1+\frac{j_m}{m}\right)^{-nm}}%
{\frac{j_m}{m}}}%
{\displaystyle\frac{\left(1+\frac{j_m}{m}\right)^{m}-1}%
{\frac{j_m}{m}}}%
= R\,\frac{a_{nm;\,{j_{m}\over m}}}%
{s_{m;\,{j_{m}\over m}}}](/sites/default/files/tex_cache/ce03c87ddec37c28a501a792408f2d42.png)
Итак, приведённая ценность рассматриваемой ренты может быть вычислена по формуле:
-срочная рента
Применяя формулы из лекций 3 и 6, получаем:
![PV = S\left(1+{j_{m}\over m}\right)^{-nm}=\frac{R}{p}\times
\frac{\left(1+{j_{m}\over m}\right)^{nm}-1}{\left(1+{j_{m}\over m}\right)^{{m\over p}}-1}
\left(1+{j_{m}\over m}\right)^{-nm}=\\[8pt]
= \frac{R}{p}\times \frac{1-\left(1+{j_{m}\over
m}\right)^{-nm}}{\left(1+{j_{m}\over m}\right)^{{m\over p}}-1}%
=\frac{R}{p}\times
\frac{\displaystyle\frac{1-\left(1+{j_{m}\over m}\right)^{-nm}}%
{\frac{j_m}{m}}}%
{\displaystyle\frac{\left(1+{j_{m}\over m}\right)^{{m\over p}}-1}%
{\frac{j_m}{m}}}=%
\frac{R}{p}\times\frac{a_{nm;\,{j_{m}\over m}}}{s_{{m\over
p};\,{j_{m}\over m}}}](/sites/default/files/tex_cache/af9aa40171685ce2e6e96f8c0c32d939.png)
Итак, приведённая ценность ренты в данном случае равна:
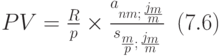
-срочная рента при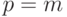 
В лекции 6 было доказано, что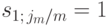 
, поэтому формула (7.6) в этом случае принимает вид:
