НОУ ИНТУИТ | Элементы финансовой математики. Лекция 7: Приведенная ценность финансовой ренты

Учитесь и получайте официальные документы БЕСПЛАТНО. Вы можете поддержать наш проект.

Регистрация Вход

Твой путь к знаниям!

Опубликован: 24.09.2017 | Доступ: свободный | Студентов: 1236 / 369 | Длительность: 12:18:00

Тема: Менеджмент

Специальности: Менеджер, Руководитель, Экономист

|

Вам нравится? Нравится 33 студентам

| Поделиться |

Поддержать курс

| Скачать электронную книгу

7.3.4 Бессрочная рента

В предыдущей лекции мы уже говорили о бессрочной ренте и приводили примеры таких рент. Очевидно, что наращенная сумма бессрочной ренты, каждый член которой равен положительному числу R, бесконечно велика, и говорить об её величине не имеет смысла. Иначе обстоит дело с современной ценностью бессрочной ренты.

Приведённой ценностью 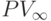$PV_{\infty}$ бессрочной ренты является сумма, которую надо вложить в начальный момент под сложные проценты по данной ставке, чтобы в дальнейшем каждый год (или каждый период начисления процентов) можно было получать с этого вклада сумму R. Приведённую ценность бессрочной ренты можно определить как предел приведённой ценности конечной ренты при неограниченном увеличении числа членов ренты. Ниже при нахождении пределов всюду используется тот факт, что 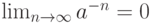$\lim_{n\rightarrow \infty} a^{-n}=0$ при любом a>1 . Рассмотрим различные некоторые виды бессрочной ренты.

Годовая рента с начислением процентов в конце каждого года по ставке сложных процентов, равной

Приведённая ценность конечной ренты этого вида определяется формулой (7.2). Найдем предел данного в этой формуле выражения при неограниченном увеличении n:

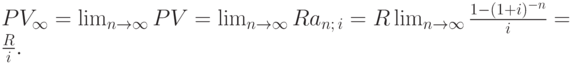
$PV_{\infty}=\lim_{n\rightarrow\infty} PV=\lim_{n\rightarrow\infty} Ra_{n;\,i}= R\lim_{n\rightarrow\infty} \frac{1-(1+i)^{-n}}{i}=\frac{R}{i}.$

Следовательно, приведённая ценность бессрочной ренты в данном случае равна:

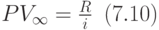
$PV_{\infty}=\frac{R}{i}\,\,\, (7.10)$

-срочная рента с начислением процентов в конце года по ставке сложных процентов, равной

Приведённая ценность бессрочной ренты в этом случае равна пределу выражения в формуле (7.3):

$PV_{\infty} = \lim_{n\rightarrow\infty} PV=\lim_{n\rightarrow\infty} Ra_{n;\,i}^{(p)}= R\lim_{n\rightarrow\infty} \frac{1-(1+i)^{-n}}{p[(1+i)^{{1\over p}}-1]}= \frac{R}{p[(1+i)^{{1\over p}}-1]}$

Воспользуемся формулой из лекции 6 и получим:

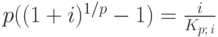
$p((1+i)^{1 /p}-1)=\frac{i}{K_{p;\,i}}$

следовательно, полученное для 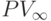$PV_{\infty}$ выражение можно переписать так:

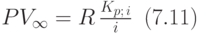
$PV_{\infty}=R\,\frac{K_{p;\,i}}{i}\,\,\, (7.11)$

Годовая рента с начислением процентов раз в год по ставке $\mbox{\boldmath j_m$

приведённая ценность бессрочной ренты в этом случае равна пределу выражения в формуле (7.5):

$PV_{\infty} = \lim_{n\rightarrow\infty} PV=\lim_{n\rightarrow\infty} R\,\frac{a_{nm;\,{j_{m}\over m}}}{s_{m;\,{j_{m}\over m}}}=\\[6pt] = R\,\lim_{n\rightarrow\infty}\frac{1-\left(1+{j_{m}\over m}\right)^{-nm}}% {\left(1+{j_{m}\over m}\right)^{m}-1}= \frac{R}{\left(1+{j_{m}\over m}\right)^{m}-1}$

Используя формулу из лекции 6, последнее равенство можно переписать и получить формулу:

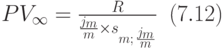
$PV_{\infty}=\frac{R}{{j_{m}\over m}\times s_{m;\,{j_{m}\over m}}}\,\,\, (7.12)$

-срочная рента с начислением процентов раз в год по ставке $\mbox{\boldmath j_m$

Приведённая ценность бессрочной ренты в этом случае равна пределу выражения из формулы (7.6):

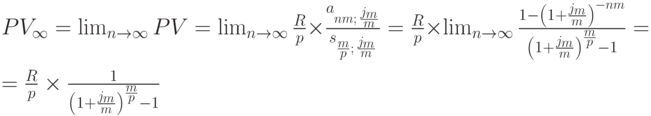
$PV_{\infty} = \lim_{n\rightarrow\infty} PV=\lim_{n\rightarrow\infty} \frac{R}{p}\times\frac{a_{nm;\,{j_{m}\over m}}}{s_{{m\over p};\,{j_{m}\over m}}}= \frac{R}{p}\times\lim_{n\rightarrow\infty} \frac{1-\left(1+{j_{m}\over m}\right)^{-nm}}% {\left(1+{j_{m}\over m}\right)^{{m\over p}}-1}=\\ = \frac{R}{p}\times\frac{1}{\left(1+{j_{m}\over m}\right)^{{m\over p}}-1}$

Используя формулу из лекции 6, последнее равенство можно переписать и получить формулу:

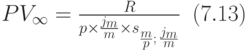
$PV_{\infty}=\frac{R}{p\times {j_{m}\over m}\times s_{{m\over p};\,{j_{m}\over m}}}\,\,\, (7.13)$

В частном случае этой ренты, когда m=p, имеет место равенство:

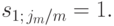
$s_{1;\,j_{m}/m}=1.$

С учётом последнего равенства формула (7.13) принимает вид:

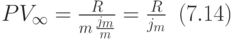
$PV_{\infty}=\frac{R}{m\,{j_{m}\over m}}=\frac{R}{j_{m}}\,\,\, (7.14)$

Годовая рента с непрерывным начислением процентов по ставке 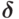$\mbox{\boldmath \delta$

Приведённая ценность бессрочной ренты в этом случае равна пределу выражения в формуле (7.8):

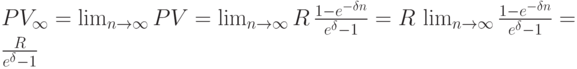
$PV_{\infty}=\lim_{n\rightarrow\infty} PV=\lim_{n\rightarrow\infty} R\,\frac{1-e^{-\delta n}}{e^{\delta}-1}= R\,\lim_{n\rightarrow\infty} \frac{1-e^{-\delta n}}{e^{\delta}-1}= \frac{R}{e^{\delta}-1}$

Следовательно, имеем формулу:

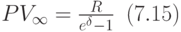
$PV_{\infty}=\frac{R}{e^{\delta}-1}\,\,\, (7.15)$

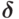
-срочная рента с непрерывным начислением процентов по ставке $\mbox{\boldmath \delta$

Приведённая ценность бессрочной ренты в этом случае равна пределу выражения в формуле (7.9):

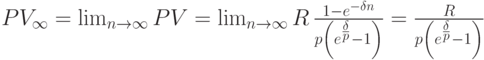
$PV_{\infty}=\lim_{n\rightarrow\infty} PV=\lim_{n\rightarrow\infty} R\,\frac{1-e^{-\delta n}}{p\left(e^{{\delta \over p}}-1\right)}= \frac{R}{p\left(e^{{\delta\over p}}-1\right)}$

Следовательно, получили формулу:

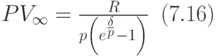
$PV_{\infty}=\frac{R}{p\left(e^{{\delta\over p}}-1\right)}\,\,\, (7.16)$

Приведем пример на использование формул для вычисления приведённой ценности бессрочной ренты.

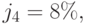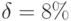Пример 65. Фирма планирует организовать специальный фонд для выплаты 1 000 000 руб. в конце года направленным на учёбу работникам. Какую сумму потребуется положить в банк, чтобы обеспечить получение указанной суммы неограниченно долго, если: а) банк выплачивает 8% годовых (сложных), б) банк выплачивает проценты по ставке $j_{4}=8\%,$ в) банк выплачивает непрерывные проценты с силой роста $\delta=8\%$ ?

Решение. а) Последовательность получаемых сумм является бессрочной рентой с начислением процентов в конце года. Применяем формулу (7.10) при R=1 000 000, i=0.08

$PV_{\infty}={R\over i}={1\,000\,000\over 0.08}=12\,500\,000 \mbox{ руб.}$

б) Последовательность получаемых сумм является бессрочной рентой с начислением процентов m раз в год по годовой ставке $j_{m}$ . Применяем формулу (7.12) при $m=4, j_{m}=8\%, j_{m}/m=8\% /4=2\%$ :

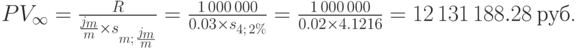
$PV_{\infty}=\frac{R}{{j_{m}\over m}\times s_{m;\,{j_{m}\over m}}}=\frac{1\,000\,000}{0.03\times s_{4;\,2\%}}% =\frac{1\,000\,000}{0.02\times 4.1216}=12\,131\,188.28\ \mbox{руб.}$

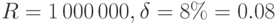в) Последовательность получаемых сумм образует бессрочную ренту с непрерывным начислением процентов по годовой ставке $\delta$ . Применяем формулу (7.15) при $R=1\,000\,000, \delta=8\%=0.08$ :

$PV_{\infty}=\frac{R}{e^{\delta}-1}=\frac{1\,000\,000}{e^{0.08}-1} =12\,006\,665.96\mbox{ руб.}$

Дальше >>

Авторизоваться

Элементы финансовой математики

Приведенная ценность финансовой ренты

7.3.4 Бессрочная рента

Вопросы и ответы