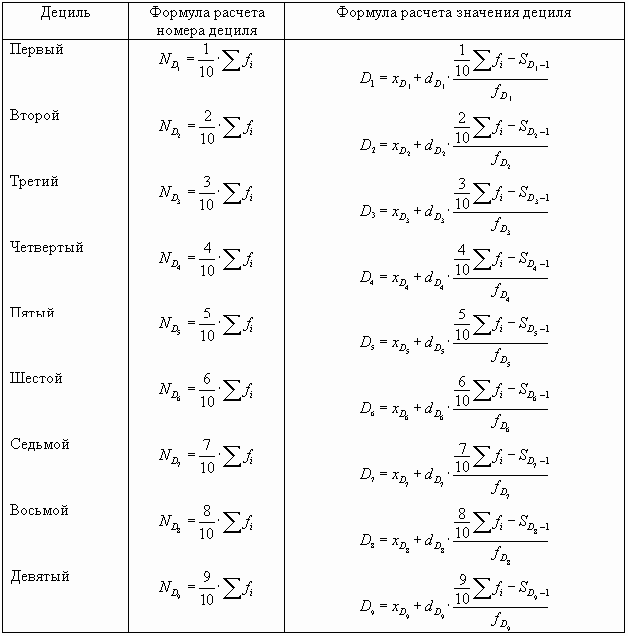|
Мне нужно изучить математическую статистику с нуля для обработки данных на компьютере. Читаю уже вторую лекцию, но пока ничего даже отдалённо близкого к моей цели не нахожу. Есть ли математическая статистика в дальнейших лекциях? Или я зря теряю время на изучение этого курса? У меня крайне ограниченный временной срок - я не могу терять время на самостоятельную проверку моего вопроса посредством изучения данного курса. |
Структурные характеристики вариационного ряда распределения
8.2. Медиана, квартили, децили
Медиана - это значение признака, которое делит статистическую совокупность на две равные части: половина единиц совокупности имеет значения признака не меньше медианы, другая половина - значения признака не больше медианы.
Значения изучаемого признака всех единиц статистической совокупности можно расположить в порядке возрастания (или убывания). В этом случае мы получим ранжированный ряд. Если число единиц совокупности нечетное, то значение признака, находящееся в середине ранжированного ряда, будет являться медианой. Если число единиц совокупности четное, то медианой будет средняя величина из двух значений признака, находящихся в середине ряда.
Пример 8.5. Имеются следующие данные о результатах сдачи экзамена по статистике в студенческой группе:
| Номер студента | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Оценка по статистике | 3 | 4 | 2 | 3 | 4 | 4 | 4 | 3 | 4 | 5 | 5 |
Представим их в виде ранжированного ряда:
Как видим, в ранжированном ряду оценки расположились следующим образом: сначала записана одна неудовлетворительная оценка (ее получил студент, имеющий в ведомости номер 3), затем три оценки "удовлетворительно", пять оценок "хорошо" и две оценки "отлично". В середине ранжированного ряда, имеющего нечетное число членов, стоит оценка "4", которую получил студент, записанный в ведомости под номером 5. Следовательно, оценка "4 (хорошо)" является медианой для данного ряда распределения. Пять студентов получили оценки 4 и ниже (2, 3, 3, 3, 4), другие пять студентов - 4 и выше (4, 4, 4, 5, 5).
Пример 8.6. Имеются данные о цене антоновских яблок в шести магазинах города. Представим их сразу в виде ранжированного ряда:
| Название магазина | "Огонек" | "Маяк" | "Заря" | "Татьяна" | "Ночной" | "Любимый" |
|---|---|---|---|---|---|---|
| Цена яблок, руб. за кг | 40 | 41 | 42 | 44 | 44 | 45 |
В середине ранжированного ряда находятся цены двух магазинов, причем они разные. Медиана определяется как средняя величина из этих значений признака. Она равна 43 руб. [(42 + 44) : 2 = 43].
Таким образом, в 50% магазинов города яблоки продаются по цене не выше 43 руб. за килограмм, а в других 50% магазинов - по цене не ниже 43 руб.
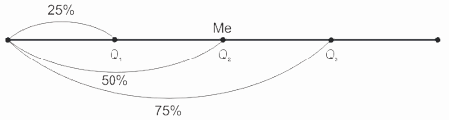
Квартили (Q) делят ранжированный ряд на четыре равные части: первый квартиль (Q1) включает значения признака, не превышающие 25% единиц совокупности, второй квартиль (Q2) - совпадает с медианой (Ме), третий квартиль (Q3) - значения признака, не превышающие 75% единиц совокупности (рис. 8.3).
Децили (D) делят ранжированный ряд на десять равных частей: первым децилем (D1) является значение признака, которое не превышает 10% единиц совокупности, вторым (D2) - 20%, третьим (D3) - 30% и т.д. При этом пятый дециль (D5) совпадает с медианой и вторым квартилем (Q2) (рис. 8.4).
Медиана, квартили и децили относятся к группе квантилей. Квантили - это показатели, которые делят вариационные ряды на определенное количество равных частей. Среди них, помимо названных, также имеются квантили, которые делят ряд на пять равных частей, перцентили - на сто и т.д.
Структурные показатели не зависят от того, имеются ли в статистической совокупности аномальные (резко выделяющиеся) наблюдения. И если средняя величина при их наличии теряет свою практическую значимость, то информативность медианы наоборот усиливается - она начинает выполнять функции средней, т.д. характеризовать центр совокупности.
Способы расчета рассматриваемых структурных показателей зависят от вида вариационного ряда. Рассмотрим их подробнее.
8.2.1. Определение структурных средних в дискретных вариационных рядах
Для определения медианы в дискретных вариационных рядах:
- находят ее порядковый номер по формуле
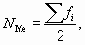
- строят ряд накопленных частот;
- находят накопленную частоту, которая равна порядковому номеру медианы или его превышает;
- варианта, соответствующая данной накопленной частоте, является медианой.
Пример 8.7. Определим медианный стаж сотрудников страховой компании на основе следующих данных:
| Время работы, лет, xi | Число сотрудников, чел., fi | Накопленная частота, Si |
|---|---|---|
| 1 | 5 | 5 |
| 2 | 7 | 12 |
| 3 | 4 | 16 |
| 4 | 9 | 25 |
| 5 | 13 | 38 |
| 6 | 10 | 48 |
| 7 | 16 | 64 |
| 8 | 13 | 77 |
| Итого | 77 | - |
Номер медианы равен
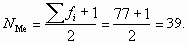
Для того чтобы найти значение варианты, стоящей на 39 месте, рассчитаем накопленные частоты. Для пятой группы накопленная частота равна 38. Это означает, что 38 работников имеют стаж работы 5 лет и меньше. Для шестой группы накопленная частота - 48 (она первая превышает порядковый номер медианы), следовательно, в эту группу входят сотрудники с порядковыми номерами от 39 до 48, в том числе и искомый 39-й сотрудник. Стаж работы сотрудников в шестой группе - 6 лет. Значит, Ме = 6. Итак, 50% сотрудников работают в данной страховой компании не более шести лет.
Квартили и децили определяют аналогично медиане: сначала находят их номер, затем среди накопленных частот ищут такую, которая первая равна или превышает порядковый номер показателя, ей соответствует варианта, которая является искомым показателем. Номера квартилей рассчитываются по формулам:
- первый (нижний) квартиль имеет номер:
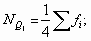
- третий (верхний) квартиль:
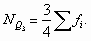
Порядковые номера децилей исчисляются следующим образом:
- для первого дециля:
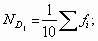
- для второго дециля:
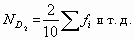
Определим квартили по данным примера 8.7. Их номера равны:
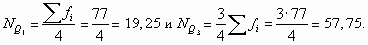
Первая накопленная частота, превышающая 19,25, равна 25. Ей соответствует варианта 4, являющаяся первым квартилем. Первая накопленная частота, которая превышает 57,75 - это 64; ей соответствует варианта, равная 7. Это третий квартиль. Итак, 25% сотрудников работают в данной компании не более четырех лет, а 75% - не более семи лет.
Аналогично определяются децили. Например, восьмой дециль вычисляется следующим образом:
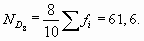
Накопленная частота 64 - первая, превышающая ND8, ей соответствует значение признака - 7 лет, т.д. у 80% сотрудников стаж работы в данной компании не превышает семи лет.
8.2.2. Определение структурных средних в интервальном вариационном ряду
В интервальных рядах сначала определяют медианный интервал. Для этого так же, как и в дискретных рядах, рассчитывают порядковый номер медианы
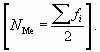
Накопленной частоте, которая равна номеру медианы или первая его превышает, в интервальном вариационном ряду соответствует медианный интервал. Обозначим эту накопленную частоту SМе. Непосредственно расчет медианы проводят по формуле:
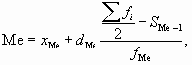
где хМе - нижняя граница медианного интервала;
dMe - величина медианного интервала;
SMe - 1 - накопленная частота интервала, предшествующего медианному;
fMe - частота медианного интервала.
Пример 8.8. По следующим данным определим медианное значение суммы выданных банками кредитов:
| Сумма выданных кредитов, млн ден. ед. | Количество банков, fi | Накопленная частота, Si. |
|---|---|---|
| 20-40 | 8 | 8 |
| 40-60 | 15 | 23 |
| 60-80 | 21 | 44 |
| 80-100 | 12 | 56 |
| 100-120 | 9 | 65 |
| 120-140 | 7 | 72 |
| 140-160 | 4 | 76 |
| Итого | 76 | - |
Проведем расчет:
- определим порядковый номер медианы
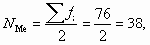
- определим накопленную частоту медианного интервала: SМе > NМе; SМе = 44;
- определим соответствующий ей медианный интервал "60-80";
- рассчитаем значение медианы по формуле
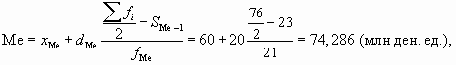
т.е. у 50% банков сумма выданных кредитов не превышает 74,286 млн ден. ед.
Далее произведем расчет квартилей и децилей в интервальном вариационном ряду.
Для приведенного интервального ряда необходимо определить:
- номер первого (нижнего) квартиля:
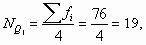
тогда ей соответствует интервал "40-60", в котором находится первый квартиль;
- номер третьего (верхнего) квартиля:
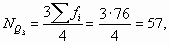
тогда ей соответствует интервал "100-120", в котором находится третий квартиль;
- первый (нижний) квартиль рассчитаем по формуле:
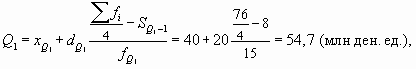
т.е. у 25% банков сумма выданных кредитов не превышает 54,7 млн ден. ед.;
- третий (верхний) квартиль рассчитаем по формуле:
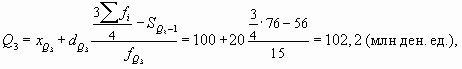
т.е. у 75% банков сумма выданных кредитов не превышает 102,2 млн ден. ед.
Аналогично квартилям определяем децили. Формулы, используемые в ходе расчетов, поместим в таблицу.
|
|
|
Здесь хD - нижняя граница децильного интервала; dD - величина децильного интервала; SD - 1 - сумма накопленных частот интервала, предшествующего децильному; fD - частота децильного интервала. |
Номер шестого дециля равен: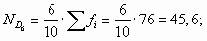 следовательно SQ6 = 56, этой накопленной частоте соответствует интервал "80-100", в котором находится шестой дециль. Величина децильного значения равна:
следовательно SQ6 = 56, этой накопленной частоте соответствует интервал "80-100", в котором находится шестой дециль. Величина децильного значения равна: 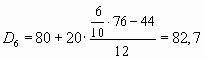 (млн ден. ед.), т.д. у 60% банков сумма выданных кредитов не превышает 82,7 млн ден. ед.
(млн ден. ед.), т.д. у 60% банков сумма выданных кредитов не превышает 82,7 млн ден. ед.
В статистике для характеристики степени неоднородности совокупности часто используют коэффициенты дифференциации (квартильные и децильные). Децильный коэффициент дифференциации представляет собой отношение девятого дециля к первому:
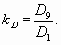
Данный коэффициент показывает, во сколько раз варианта, выше которой находятся 10% единиц совокупности, имеющих самые большие значения признака, больше варианты, ниже которой находятся 10% единиц совокупности с самыми маленькими значениями признака. Аналогично квартильный коэффициент дифференциации определяется как отношение третьего квартиля к первому.
В заключение отметим, что приблизительное равенство средней арифметической, моды и медианы, рассчитанных по отношению к одному и тому же ряду, говорит о том, что значения признака в изучаемой совокупности имеют нормальный закон распределения (или приближаются к нему).
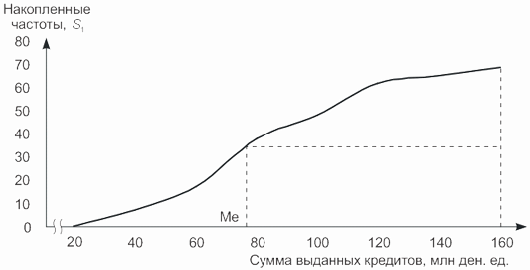
Медиана может быть определена графически по кумуляте. Для этих целей на оси ординат, где отмечаются накопленные частоты, находится точка, соответствующая полусумме всех частот (т.е. порядковому номеру медианы). Из нее проводится прямая параллельно оси абсцисс до пересечения с графиком (кумулятой распределения). Абсцисса точки пересечения соответствует медиане данного ряда распределения.