НОУ ИНТУИТ | Статистика. Лекция 7: Показатели вариации в статистике

Учитесь и получайте официальные документы БЕСПЛАТНО. Вы можете поддержать наш проект.

Регистрация Вход

Твой путь к знаниям!

Опубликован: 13.05.2017 | Доступ: свободный | Студентов: 1743 / 811 | Длительность: 13:46:00

Темы: Математика, Экономика, Менеджмент

Специальности: Менеджер, Экономист

|

Вам нравится? Нравится 40 студентам

| Поделиться |

Поддержать курс

| Скачать электронную книгу

Аннотация: В процессе статистического анализа может сложиться ситуация, когда значения средних величин совпадают, а совокупности, на основе которых они рассчитаны, состоят из единиц, значения признака у которых достаточно резко различаются между собой. Возьмем, например, данные о количестве договоров, заключенных в двух филиалах страховой компании. Предположим, что в каждом из филиалов работает по два агента. В первом филиале один агент заключил 5 договоров, а второй - 25; во втором филиале каждый агент заключил по 15 договоров. Как видим, среднее число договоров, заключенных одним агентом в каждом филиале совпадает (15 договоров), в то же время очевидно, что первая и вторая совокупности качественно неоднородны, т.д. вариация значений признака внутри них различна. Данная глава посвящена рассмотрению показателей, с помощью которых можно оценить и измерить вариацию признака.

Ключевые слова: ПО, дисперсия, разность, интерпретация, значение, коэффициент вариации

7.1. Абсолютные и относительные показатели вариации

Рассмотрим две совокупности сотрудников рекламных агентств.

Распределение сотрудников первого агентства по уровню месячной заработной платы представлено в табл. 7.1.

Таблица 7.1. Распределение сотрудников первого агентства по уровню месячной заработной платы
Размер месячной заработной платы, руб.	Середина интервала, x_i	Число сотрудников, чел., f_i	x_i*f_i
4 000-6 000	5 000	10	50 000
6 000-8 000	7 000	6	42 000
8 000-10 000	9 000	19	171 000
10 000-12 000	11 000	26	286 000
14 000-16 000	15 000	10	150 000
16 000-18 000	17 000	5	85 000
Сумма	-	95	1 031 000

Распределение сотрудников второго агентства по уровню месячной заработной платы представлено в табл. 7.2.

Таблица 7.2. Распределение сотрудников второго агентства по уровню месячной заработной платы
Размер месячной заработной платы, руб.	Середина интервала, x_i	Число сотрудников, чел., f_i	x_i*f_i
1 500-4 500	3 000	9	27 000
4 500-7 500	6 000	26	156 000
7 500-10 500	9 000	24	216 000
10 500-13 500	12 000	18	216 000
13 500-16 500	15 000	14	210 000
16 500-19 500	18 000	10	180 000
19 500-22 500	21 000	9	189 000
Сумма	-	110	1 194 000

Рассчитаем средний уровень заработной платы:

для первого агентства:
для второго агентства:

Как видим, средние в двух совокупностях практически совпадают между собой (с разницей в 1 руб.). Однако если вы вдруг случайно встретите сотрудников этих агентств и поинтересуетесь уровнем оплаты их труда, то вас заверят, что платят у них вовсе не одинаково! Почему?! Оказывается, что разброс значений вокруг средней в этих совокупностях абсолютно разный. Значит, такой характеристики, как средняя, вовсе не достаточно, чтобы делать выводы о совокупности. Для этого используют показатели вариации.

Вариацией называется изменчивость значений признака у единиц статистической совокупности. Для измерения величины вариации используются абсолютные и относительные показатели вариации.

К абсолютным показателям вариации относятся размах вариации, среднее линейное отклонение, дисперсия, среднее квадратическое отклонение.

Размах вариации (R) вычисляется как разность между максимальным и минимальным значениями признака

$R=x_{max} -x_{min}$

( 7.1)

Среднее линейное отклонение (d) представляет собой среднюю арифметическую величину из абсолютных значений отклонений отдельных значений признака от их средней. Если данные не сгруппированы, то рассчитывается невзвешенное среднее линейное отклонение

$\overline{d}_{прост.}=\frac {\sum (x_i-\overline{x})} n$

( 7.2)

Для сгруппированных данных, представленных в виде вариационного ряда, используется взвешенное среднее линейное отклонение, где весами выступают частоты соответствующих вариант:

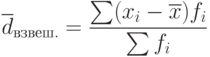$\overline{d}_{взвеш.}=\frac {\sum (x_i-\overline{x})f_i} {\sum f_i}$

( 7.3)

Дисперсией (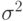 $\sigma^{2}$ ) называется средняя арифметическая величина, полученная из квадратов отклонений значений признака от их средней

для несгруппированных данных:

$\sigma_{прост.}^2=\frac {\sum (x_i-\overline{x})^2} n$ ( 7.4)
для сгруппированных данных:
$\sigma_{взвеш.}^2=\frac {\sum (x_i-\overline{x})^2 f_i} {\sum f_i}$ ( 7.5)

Квадратный корень из дисперсии называется средним квадратическим отклонением (его называют также стандартным отклонением):

для несгруппированных данных:
$\sigma_{прост.}=\sqrt{\frac {\sum (x_i-\overline{x})^2} n}$ ( 7.6)
для сгруппированных данных:
$\sigma_{взвеш.}=\sqrt{\frac {\sum (x_i-\overline{x})^2 f_i} {\sum f_i}}$ ( 7.7)

Абсолютные показатели вариации, за исключением дисперсии, имеют те же единицы измерения, что и исследуемый показатель вариационного ряда. Поэтому, если экономическая интерпретация, например, среднего линейного отклонения, проста и понятна физически, то в случае с дисперсией она затруднена. Однако дисперсия рассчитывается в статистическом анализе гораздо чаще, чем другие показатели вариации. Связано это с тем, что дисперсия широко используется в таких видах статистического анализа, как корреляционный, регрессионный, дисперсионный, при оценках результатов выборочного наблюдения. Кроме того, именно с помощью дисперсии можно оценить влияние случайных и систематических факторов на формирование значений случайной величины.

Для сравнения вариации одного и того же показателя в разных совокупностях (например, заработной платы двух рекламных агентств) или вариации разных показателей в одной совокупности (например, вариации заработной платы и возраста в одном рекламном агентстве) используют относительные показатели вариации. К ним относят:

коэффициент осцилляции:
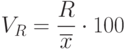
$V_R=\frac R {\overline {x}} \cdot 100%$ ( 7.8)
относительное линейное отклонение:
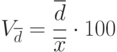
$V_{\overline {d}}=\frac {\overline {d}} {\overline {x}} \cdot 100%$ ( 7.9)
коэффициент вариации:
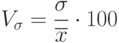
$V_{\sigma}=\frac \sigma {\overline {x}} \cdot 100%$ ( 7.9)

Принято считать, что если значение 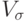$V_{\sigma}$ &> 33%, то совокупность неоднородна, и для дальнейшего статистического анализа следует либо исключить крайние значения признака, либо разбить совокупность на однородные группы (требование однородности данных присутствует практически во всех видах статистического анализа).

Рассчитаем показатели вариации для приведенных в табл. 7.1 и 7.2 вариационных рядов (табл. 7.3 и 7.4).

Таблица 7.3. Расчет абсолютных и относительных показателей вариации для первого агентства
Размер месячной заработной платы, руб.	Середина интервала, x_i	Число сотрудников, чел., y_j	(x_i-x)*f	(x_i-x)²*f
4 000-6 000	5 000	10	58 530	342 576 090
6 000-8 000	7 000	6	23 118	89 073 654
8 000-10 000	9 000	19	35 207	65 238 571
10 000-12 000	11 000	26	3 822	561 834
12 000-14 000	13 000	19	40 753	87 582 571
14 000-16 000	15 000	10	41 470	171 976 090
16 000-18 000	17 000	5	30 735	188 928 045
Сумма	-	95	233 675	945 936 855

По первому агентству получим следующие данные.

Размах вариации:

R = x_max - x_min = 18 000 - 4000 = 14 000 (руб.).

Среднее линейное отклонение (так как ряд сгруппирован и частоты не равны между собой) рассчитываем как взвешенную величину:

Дисперсия:

Среднее квадратическое отклонение:

Коэффициент осцилляции:

Относительное линейное отклонение:

Коэффициент вариации:

Судя по коэффициенту вариации, совокупность по данному признаку можно считать однородной.

Проведем расчет аналогичных характеристик вариации по второму агентству (табл. 7.4).

Таблица 7.4. Расчет абсолютных и относительных показателей вариации для второго агентства
Размер месячной заработной платы, руб.	Середина интервала, x_i	Число сотрудников, чел., y_j	(x_i - x)*f	(x_i - x)²*f
1 500-4 500	3 000	9	70 686	555 167 844
4 500-7 500	6 000	26	126 204	612 594 216
7 500-10 500	9 000	24	44 496	82 495 584
10 500-13 500	12 000	18	20 628	23 639 688
13 500-16 500	15 000	14	58 044	240 650 424
16 500-19 500	18 000	10	71 460	510 653 160
19 500-22 500	21 000	9	91 314	926 471 844
Сумма	-	110	482 832	2 951 672 760

Показатели вариации по второму агентству:

Размах вариации:

R = 22 500 - 1500 = 21 000 (руб.);

Среднее линейное отклонение:

Дисперсия:

Среднее квадратическое отклонение - 5180 (руб.).

Коэффициент осцилляции - 193%.

Относительное линейное отклонение - 40%.

Коэффициент вариации - 48%.

Таким образом, по данному признаку вторая совокупность сотрудников неоднородна.

Сравнение относительных показателей вариации по двум совокупностям говорит о том, что дифференциация по уровню заработной платы во втором агентстве гораздо выше, чем в первом, хотя их средние практически совпадают между собой.

Дальше >>

Авторизоваться

Статистика

Показатели вариации в статистике

7.1. Абсолютные и относительные показатели вариации

Вопросы и ответы