|
При переходе на страницу 2 после изучения постоянных издержек, лекция сразу "говорит" о технологическом процессе. кроме того, в имеющейся лекции нет формул, задачи на которые в большом количестве представлены в тесте |
Риски предпринимательства и обеспечение его безопасности
Дисперсия - характеризует степень колеблемости изучаемого показателя (в данном случае – ожидаемого дохода от осуществления финансовой операции) по отношению к его средней величине. Чем колебания больше, тем выше степень риска. Дисперсия рассчитывается по следующей формуле:
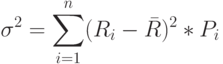
где  – дисперсия;
– дисперсия;  – конкретное значение возможных вариантов ожидаемого дохода по рассматриваемой финансовой операции;
– конкретное значение возможных вариантов ожидаемого дохода по рассматриваемой финансовой операции;  - среднее ожидаемое значение дохода по рассматриваемой финансовой операции;
- среднее ожидаемое значение дохода по рассматриваемой финансовой операции;  – возможная частота (вероятность) получения отдельных вариантов ожидаемого дохода по финансовой операции;
– возможная частота (вероятность) получения отдельных вариантов ожидаемого дохода по финансовой операции; 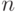 – число наблюдений.
– число наблюдений.
Дисперсия не даёт полной картины уклонений 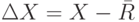 , более наглядных для оценивания рисков. Тем не менее, задание дисперсии позволяет установить связь между линейным и квадратичным отклонениями с помощью известного неравенства Чебышева.
, более наглядных для оценивания рисков. Тем не менее, задание дисперсии позволяет установить связь между линейным и квадратичным отклонениями с помощью известного неравенства Чебышева.
Вероятность того, что случайная величина X отклоняется от своего математического ожидания больше, чем на заданный допуск  , не превосходит её дисперсии, делённой на
, не превосходит её дисперсии, делённой на  , т.е.
, т.е.

Отсюда видно, что незначительному риску по дисперсионному отклонению соответствует малый риск по линейным отклонениям [30]: точки  с большой вероятностью будут располагаться внутри
с большой вероятностью будут располагаться внутри 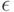 – окрестности ожидаемого значения
– окрестности ожидаемого значения  .
.
Среднеквадратическое (стандартное) отклонение является одним из наиболее распространенных при оценке уровня индивидуального финансового риска, как и дисперсия определяет степень абсолютной колеблемости и рассчитывается по следующей формуле [2, 26]:

Среднеквадратическое отклонение  является размерной величиной и указывается в тех же единицах, в каких измеряется варьирующий признак. Преимущество среднеквадратического отклонения в том, что при близости наблюдаемого распределения (например, распределении дохода от инвестиций) к нормальному этот параметр может быть использован для определения границ, в которых с заданной вероятностью следует ожидать значение случайной переменной. Так, например, с вероятностью 68,3% можно утверждать, что значение случайной переменной
является размерной величиной и указывается в тех же единицах, в каких измеряется варьирующий признак. Преимущество среднеквадратического отклонения в том, что при близости наблюдаемого распределения (например, распределении дохода от инвестиций) к нормальному этот параметр может быть использован для определения границ, в которых с заданной вероятностью следует ожидать значение случайной переменной. Так, например, с вероятностью 68,3% можно утверждать, что значение случайной переменной  (в нашем случае доход) находится в границах
(в нашем случае доход) находится в границах  , а с вероятностью 95,4% - в пределах
, а с вероятностью 95,4% - в пределах 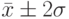 и т.д. [39]. Сказанное иллюстрируется на Рис. 10.2
и т.д. [39]. Сказанное иллюстрируется на Рис. 10.2
Коэффициент вариации  - позволяет определить уровень риска, если показатели среднего ожидаемого дохода от осуществления финансовых операций различаются между собой [26]. Расчёт коэффициента вариации осуществляется по следующей формуле:
- позволяет определить уровень риска, если показатели среднего ожидаемого дохода от осуществления финансовых операций различаются между собой [26]. Расчёт коэффициента вариации осуществляется по следующей формуле:
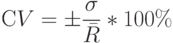
Коэффициент вариации  – безразмерная величина. С его помощью можно сравнивать даже колеблемость признаков, выраженных в разных единицах измерения. Коэффициент вариации изменяется от 0 до 100%. Чем больше коэффициент, тем сильнее колеблемость. Установлена следующая качественная оценка различных значений коэффициента вариации: до 10% - слабая колеблемость, 10 - 25% - умеренная колеблемость, свыше 25% - высокая колеблемость [40].
– безразмерная величина. С его помощью можно сравнивать даже колеблемость признаков, выраженных в разных единицах измерения. Коэффициент вариации изменяется от 0 до 100%. Чем больше коэффициент, тем сильнее колеблемость. Установлена следующая качественная оценка различных значений коэффициента вариации: до 10% - слабая колеблемость, 10 - 25% - умеренная колеблемость, свыше 25% - высокая колеблемость [40].
Бета-коэффициент (или бета) - позволяет оценить индивидуальный или портфельный систематический финансовый риск по отношению к уровню риска финансового рынка в целом. Этот показатель используется обычно для оценки рисков инвестирования в отдельные ценные бумаги и рассчитывается по формуле-

где  – бета-коэффициент;
– бета-коэффициент;  – степень корреляции между уровнем доходности по индивидуальному виду ценных бумаг (или по их портфелю) и средним уровнем доходности данной группы фондовых инструментов по рынку в целом [36];
– степень корреляции между уровнем доходности по индивидуальному виду ценных бумаг (или по их портфелю) и средним уровнем доходности данной группы фондовых инструментов по рынку в целом [36];  – среднеквадратическое отклонение доходности по индивидуальному виду ценных бумаг (или по их портфелю в целом);
– среднеквадратическое отклонение доходности по индивидуальному виду ценных бумаг (или по их портфелю в целом);  – среднеквадратическое отклонение доходности по фондовому рынку в целом.
– среднеквадратическое отклонение доходности по фондовому рынку в целом.
Уровень финансового риска отдельных ценных бумаг определяется на основе следующих значений бета-коэффициентов: 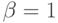 – средний уровень;
– средний уровень;  – высокий уровень;
– высокий уровень;  – низкий уровень.
– низкий уровень.
С помощью вероятностного метода оценки можно оценить риск не только конкретной сделки, но и предпринимательской фирмы в целом (проанализировав динамику её доходов) за некоторый промежуток времени. Выбор конкретных методов оценки определяется наличием необходимой информационной базы и уровнем квалификации управленческого персонала.
Традиционные для практики финансового риск-менеджмента методы оценки меры риска на основе показателя его уровня имеют ряд недостатков. К числу основных из таких недостатков относится прежде всего то, что уровневые показатели риска не характеризуют максимально возможную сумму финансового ущерба при наступлении рискового события, соответственно, не позволяют и страховаться от финансового риска предприятия в полном его объёме. Кроме того, отдельные "уровневые" показатели не могут быть агрегированы по портфелю финансовых инструментов, обращающихся на различных видах финансового рынка (например, на валютном и фондовом), а также по различным инструментам даже одного вида финансового рынка (например, опциона и свопа). Наконец, использование "уровневых" показателей меры финансового риска в процессе его контроля на предприятии является недостаточно надёжным по таким финансовым инструментам, которые чувствительны к различным факторам риска.
В связи с этим в последнее десятилетие получила развитие новая методология оценки меры финансового риска на основе использования показателя "стоимость риска" или "стоимость под риском" (Value-at-risk, VAR). Начало внедрения этой новой методологии оценки меры риска в практику связывается с директивой Европейского совета от 1993 г. (ЕЕС-6-9З), предписывающей финансовым институтам (в первую очередь банкам, инвестиционным и страховым компаниям) устанавливать обязательное резервирование капитала для обеспечения рыночных (систематических) финансовых рисков на основе расчёта показателя VAR по предложенной им методике. Впоследствии (в 1995 г.) Базельский комитет по надзору за банками [36] разрешил коммерческим банкам применять собственный методический инструментарий расчета показателя VAR.
За прошедшее десятилетие оценка меры финансового риска на основе показателя VAR получила развитие в США и Западной Европе не только в среде финансовых институтов, но и в значительном числе компаний, функционирующих в реальном секторе экономики. Кроме того методический инструментарий оценки VAR начал использоваться западными компаниями для исследования не только рыночного (систематического) риска, но и риска несистематического (в частности, для оценки кредитного риска). В последние годы использование этого показателя получает развитие и в нашей стране.
Рассмотрим основное содержание концепции и методический инструментарий оценки меры финансового риска на основе показателя VAR. Стоимость под риском представляет собой показатель статистической оценки выраженный в денежной форме максимально возможного размера финансовых потерь при установленном виде распределения вероятности факторов, влияющих на стоимость активов (инструментов), а также заданном уровне вероятности возникновения этих потерь на протяжении расчетного периода времени.
Из приведённого определения видно, что основу методологии расчёта показателя VAR составляют три основных элемента. Одним из таких элементов является установленный риск-менеджером вид распределения вероятностей рисковых факторов, влияющих на стоимость активов (инструментов) или их совокупного портфеля. Такими видами могут быть нормальное распределение, распределение Лапласа, Стьюдента и др. Поэтому для определения используемого вида распределения вероятностей предварительно должно быть проведено статистическое исследование влияния изменения рискового фактора на изменение стоимости отдельного актива или всего их портфеля. На основе такого статистического исследования должна быть построена функция ценообразования актива (или портфеля) в зависимости от конкретного фактора (вида) финансового риска. Если же показатель VAR определяется по всей совокупности факторов риска (например, при оценке систематического риска в целом), то следует определить форму и тесноту корреляционных связей между различными факторами риска. Корректность устанавливаемого вида распределения вероятностей в модели расчета показателя VAR прямо определяет правильность его значений [36].
Вторым элементом, который используется в статистической модели определения показателя VAR, является задаваемый риск-менеджером уровень вероятности того, что максимально возможный размер финансовых потерь не превысит расчётное значение этого показателя. В терминологии финансового риск-менеджмента такая заданная вероятность характеризуется термином доверительный уровень [confidence level]. Конкретное значение доверительного уровня для модели расчета показателя VAR выбирается риск-менеджером исходя из его рисковых предпочтений. В современной практике финансового риск-менеджмента этот уровень устанавливается обычно в пределах 95 - 99%.
Наконец, третьим элементом модели определения показателя VAR является устанавливаемый риск-менеджером расчетный период времени его оценки (или конкретный временной горизонт, в рамках которого оцениваются предстоящие возможные финансовые потери). В терминологии финансового риск-менеджмента такой отрезок времени характеризуется термином „период поддержания позиции" [holding реriod]. В современной практике финансового риск-менеджмента этот период определяют обычно по одному из следующих двух критериев: намечаемого периода владения рассматриваемым активом (т.е. времени его удержания в портфеле предприятия) или уровня его ликвидности (реального срока его конверсии в денежную форму без потери своей текущей рыночной стоимости).
Наглядное представление о формировании показателя VAR с учетом рассмотренных трех элементов его расчетной модели даёт график, представленный на Рис. 10.3.
Как видно из приведенного графика на Рис. 10.3, кривая доходов иллюстрирует нормальный вид распределения вероятностей при6ыли и убытков по рассматриваемому финансовому инструменту в заданном расчётном периоде времени. Поле внутри этого графика между значением  и
и 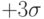 соответствует избранному доверительному уровню (95% площади под кривой), а поле между -
соответствует избранному доверительному уровню (95% площади под кривой), а поле между - и
и  — характеризует значения возможных убытков, выходящие за рамки доверительного уровня (5%). На графике показатель VAR определён в сумме 3 тыс. рублей, что соответствует максимальному размеру возможных финансовых потерь по рассматриваемому финансовому инструменту при заданных доверительном уровне и расчетном периоде оценки, при этом значение VAR отделяет на диаграмме значение доходов, выходящих за пределы доверительного интервала (10%).
— характеризует значения возможных убытков, выходящие за рамки доверительного уровня (5%). На графике показатель VAR определён в сумме 3 тыс. рублей, что соответствует максимальному размеру возможных финансовых потерь по рассматриваемому финансовому инструменту при заданных доверительном уровне и расчетном периоде оценки, при этом значение VAR отделяет на диаграмме значение доходов, выходящих за пределы доверительного интервала (10%).
Для того чтобы полностью описать риск, используя меру VAR, вначале нужно задать вероятность (достаточно малую, чтобы считать событие "почти" невозможным), или доверительный уровень, связанный с этим значением вероятности [41]. Чаще всего на практике задают вероятность 5%, соответственно, говорят о доверительном уровне 95% (100 - 5%) и обозначают результат в виде 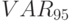 (произносится "VAR на уровне 95%"). Уровень 95% достаточно условен, каждый индивидуум задает этот уровень, исходя из собственного отношения к возможным маловероятным событиям и понимания того, что считать "почти" невозможным событием, поэтому могут использоваться и другие уровни доверительной вероятности, например 90% или 99% (тогда говорят о
(произносится "VAR на уровне 95%"). Уровень 95% достаточно условен, каждый индивидуум задает этот уровень, исходя из собственного отношения к возможным маловероятным событиям и понимания того, что считать "почти" невозможным событием, поэтому могут использоваться и другие уровни доверительной вероятности, например 90% или 99% (тогда говорят о  или
или  ). Кроме того, при оценке или вычислении VAR на практике задают временной горизонт игры (финансовой операции). Поэтому говорят о риске как о минимальном результате,
который будет получен с определенной доверительной вероятностью в течение установленного промежутка времени.
). Кроме того, при оценке или вычислении VAR на практике задают временной горизонт игры (финансовой операции). Поэтому говорят о риске как о минимальном результате,
который будет получен с определенной доверительной вероятностью в течение установленного промежутка времени.


![Графический метод определения значения показателя " стоимость под риском" [VAR]](/EDI/25_02_18_1/1519510898-10343/tutorial/735/objects/10/files/10_03.jpg)