Нейрофизиологический и формально-логический базис нейроподобных вычислений
4.6. Входное преобразование формального нейрона как генератор кратных транспозиций в лексикографически упорядоченной последовательности значений свертки
Выделив в (4.5) в качестве доминирующей составляющей  и используя аппарат индексных зон, А.Т. Бахарев показал [80,
81]:
и используя аппарат индексных зон, А.Т. Бахарев показал [80,
81]:
- Задачи 1 и 2 абстрактного синтеза (М)ПМ можно решать по критериям
 и
и  соответственно и как чисто дискретные на множестве перестановок индексов
соответственно и как чисто дискретные на множестве перестановок индексов  , не ограничив при этом непрерывные вариации
, не ограничив при этом непрерывные вариации  на этапе физического синтеза или настройки (М)ПМ.
на этапе физического синтеза или настройки (М)ПМ. - При решении задачи 3 критерий (4.7) можно дополнить максимумом функциональной устойчивости (М)ПМ при фиксированной системе решающих правил, что соответствует выбору
 , лежащих на медианах (гипер)пирамид, отобранных по критерию
, лежащих на медианах (гипер)пирамид, отобранных по критерию  , что гарантирует устойчивую реализацию
, что гарантирует устойчивую реализацию 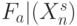 при максимальном разбросе реальных физических величин
при максимальном разбросе реальных физических величин  и
и  .
.
Точное решение модифицированной таким образом задачи оптимального синтеза (М)ПМ удалось найти [80,
81] для  , а квазиоптимальное решение для
, а квазиоптимальное решение для  , что было вызвано как ограничениями метода случайного поиска, так и уровнем использованных вычислительных средств. Для сравнения, японские ученые, проводившие достаточно интенсивные исследования в этой области, в тот же период времени смогли достичь показателей
, что было вызвано как ограничениями метода случайного поиска, так и уровнем использованных вычислительных средств. Для сравнения, японские ученые, проводившие достаточно интенсивные исследования в этой области, в тот же период времени смогли достичь показателей  ,
,  [82,
83].
[82,
83].
В современных условиях актуальными стали исследования формальных нейронов, у которых число входов исчисляется десятками [84], а незнание структуры индексных зон имеет два негативных последствия:
- При завышенной точности
 и неудачной стратегии сканирования в векторном пространстве
и неудачной стратегии сканирования в векторном пространстве 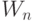 увеличивается время поиска
увеличивается время поиска  , удовлетворяющих
, удовлетворяющих  , за счет многократного и дорогостоящего анализа эквивалентных ситуаций в одной и той же индексной зоне.
, за счет многократного и дорогостоящего анализа эквивалентных ситуаций в одной и той же индексной зоне. - При заниженной точности сканирования можно пропустить часть индексных зон, что приводит к недоиспользованию функциональных возможностей элементов сети и, как следствие, к падению коэффициента использования оборудования.
Преодоление или хотя бы ослабление указанных проблем может приблизить нас к более эффективному управлению ресурсами (супер) нейрокомпьютеров, в которых по предварительным оценкам количество формальных нейронов может быть порядка  , а количество входов у каждого из них - порядка
, а количество входов у каждого из них - порядка  .
.
Введем комбинаторную схему прямого порождения транспозиций значений свертки на скалярной оси 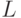 и дадим точную оценку количества таких транспозиций [85].
и дадим точную оценку количества таких транспозиций [85].
Чтобы получить все множество перестановок индексов  , генерируемых оператором линейной свертки, требуется еще процедура отбора комбинаций совместных транспозиций.
, генерируемых оператором линейной свертки, требуется еще процедура отбора комбинаций совместных транспозиций.
Комбинаторная схема порождения транспозиций значений свертки на скалярной оси  базируется на двух известных утверждениях:
базируется на двух известных утверждениях:
Утверждение 4.1. При сложении двух и более неравенств, одно из
которых противоположного знака (  и
и  ), результирующее неравенство (
), результирующее неравенство (  ) может быть произвольного знака
( аддитивный источник транспозиции -
) может быть произвольного знака
( аддитивный источник транспозиции -  -источник и
-источник и  -транспозиция соответственно). Утверждение 4.2. При умножении двух и более неравенств, одно из которых противоположного знака
(
-транспозиция соответственно). Утверждение 4.2. При умножении двух и более неравенств, одно из которых противоположного знака
(  и
и  ), результирующее неравенство
), результирующее неравенство  ) может быть произвольного знака (мультипликативный источник транспозиции -
) может быть произвольного знака (мультипликативный источник транспозиции -  -источник и
-источник и  -транспозиция соответственно).
-транспозиция соответственно).
Схему порождения транспозиций сначала построим для классов БФ, где задействован только  -источник, а затем обобщим ее на случай
-источник, а затем обобщим ее на случай 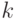 -значных ЛФ, где срабатывают еще
-значных ЛФ, где срабатывают еще  -источник и
-источник и  -источник.
-источник.
В качестве образующей комбинаторной схемы порождения транспозиций выберем систему неравенств:
 |
( 4.10)) |
считая, что 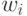 удовлетворяют условию линейной независимости:
удовлетворяют условию линейной независимости:
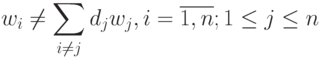 |
( 4.11)) |
где  ,
, 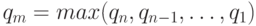 .
.
Тогда  , если
, если 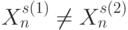 , а реализуемое оператором линейной свертки отображение
, а реализуемое оператором линейной свертки отображение  - изоморфно и обеспечивает строгий порядок следования (по
- изоморфно и обеспечивает строгий порядок следования (по  )
)  на скалярной оси
на скалярной оси 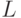 . В частности, отвечающее (4.10) и (4.11) каноническое правило присвоения значений компонентам весового вектора
. В частности, отвечающее (4.10) и (4.11) каноническое правило присвоения значений компонентам весового вектора  ,
,  обеспечивает лексикографический порядок следования
обеспечивает лексикографический порядок следования 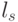 на оси
на оси  .
.
Для булевых входных векторов с 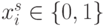 :
:
- Каноническое правило имеет вид:

- Соотношение (4.11) говорит о том, что любую компоненту весового вектора нельзя представить в виде суммы произвольного числа компонент этого вектора с меньшими значениями индексов из (4.10).
- Суммирование в (4.4) выполняется на одно-, двух-, трех-, …,
 -элементных подмножествах из (4.10) в зависимости от количества
-элементных подмножествах из (4.10) в зависимости от количества  в
в 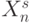 , удовлетворяющих условию
, удовлетворяющих условию  то есть
то есть - Отношение порядка между произвольными
 и
и  зависит от состава
зависит от состава  и
и  , участвующих в суммировании в (4.4), что задается булевыми векторами
, участвующих в суммировании в (4.4), что задается булевыми векторами  и
и  .
. - Числа
 и
и  специфицируют тип участвующих в транспозиции
специфицируют тип участвующих в транспозиции  значений свертки, указывая только количество
значений свертки, указывая только количество 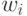 , формирующих
, формирующих  и
и 
 |
( 4.12) |
где взятые в скобки цифры (1) и (2) задают принадлежность индексируемого объекта к левой и правой части неоднозначного неравенства  .
.
Для (4.10) справедливы:
Утверждение 4.3. Сумма любого количества
(  )
) 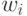 с младшими значениями индексов
с младшими значениями индексов  может быть как меньше, так и больше любого
может быть как меньше, так и больше любого 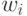 (
( 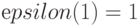 ) со старшим значением индекса
) со старшим значением индекса  .
.
Утверждение 4.4. Для любой комбинации значений е(1) и е(2), удовлетворяющих (4.12), всегда найдется хотя бы одна пара  и
и  с взаимно исключающими индексами
с взаимно исключающими индексами  (
(  ), для которых
), для которых  .
.
Утверждение 4.4 исходит из того, что при любых
(  ) всегда найдутся
) всегда найдутся  и
и  c взаимно исключающими индексами
c взаимно исключающими индексами  , которые можно разбить на непересекающиеся подмножества
, которые можно разбить на непересекающиеся подмножества  такие, что
такие, что 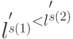 , а
, а  , то есть
, то есть 
На основе этих утверждений можно построить  -спецификацию
-спецификацию  , задающую множество всех допустимых транспозиций
, задающую множество всех допустимых транспозиций  значений свертки булевых векторов на скалярной оси
значений свертки булевых векторов на скалярной оси 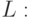
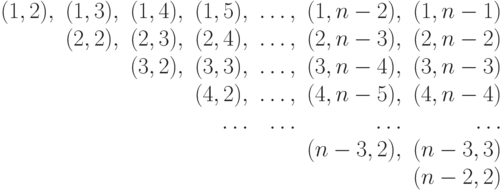 |
( 4.13) |
в которой каждая строка идентифицируется  , а каждый столбец -
, а каждый столбец -  ,
,  . Каждому элементу 1-й строки
. Каждому элементу 1-й строки  -спецификации (4.13) соответствует
-спецификации (4.13) соответствует
 |
( 4.14) |
комбинаций  и
и  , удовлетворяющих утверждению 4.3, где
, удовлетворяющих утверждению 4.3, где  - число сочетаний из
- число сочетаний из  элементов
элементов 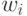 по
по  , а
, а  - текущий индекс, который связан со значением "старшего" индекса
- текущий индекс, который связан со значением "старшего" индекса  в утверждении 3 соотношением:
в утверждении 3 соотношением: 
Соотношение (4.14) иллюстрирует
табл. 4.2, где представлены все  -транспозиции сверток булевых векторов типа (
-транспозиции сверток булевых векторов типа (  ,
,  ) для
) для  . (Все численные результаты получены совместно с И. Клейменовым и А. Саломатовым.)
. (Все численные результаты получены совместно с И. Клейменовым и А. Саломатовым.)
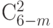 |
Транспозиции типа 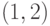
|
 |
Транспозиции типа 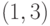
|
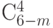 |
Транспозиции типа 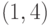
|
|---|---|---|---|---|---|
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
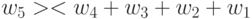 |
 |
 |
 |
 |
 |
|
 |
 |
 |
 |
Транспозиции типа 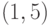
|
|
 |
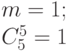 |
 |
|||
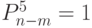 | |||||
Взяв в качестве образующей каждую  -транспозицию типа (
-транспозицию типа ( 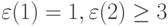 ) и переставив в них справа налево любую из компонент
) и переставив в них справа налево любую из компонент 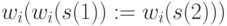 , можно получить все
, можно получить все  -транспозиции типа (
-транспозиции типа (  ), которые отвечают 2-й строке
), которые отвечают 2-й строке  -спецификации (4.13). Таких
-спецификации (4.13). Таких  -транспозиций в каждом столбце ?-спецификации будет
-транспозиций в каждом столбце ?-спецификации будет  . Исключением является 2-й столбец, где
. Исключением является 2-й столбец, где  -транспозиции типа (
-транспозиции типа ( 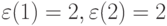 ) образованы из
) образованы из  -транспозиции типа (
-транспозиции типа ( 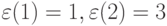 ) перестановкой справа налево одной, самой "младшей" по (4.10) компоненты, что порождает
) перестановкой справа налево одной, самой "младшей" по (4.10) компоненты, что порождает  производных
производных  -транспозиций (табл. 4.3).
-транспозиций (табл. 4.3).
Продолжив процедуру перестановок справа налево различных двоек, троек и т. д. 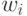 , можно убедиться, что каждая образующая
, можно убедиться, что каждая образующая  -транспозиция 1-й строки
-транспозиция 1-й строки  -спецификации порождает, включая и самих себя, подклассы
-спецификации порождает, включая и самих себя, подклассы  -транспозиций, причем мощности этих подклассов по каждому столбцу
-транспозиций, причем мощности этих подклассов по каждому столбцу  -спецификации образуют ряд:
-спецификации образуют ряд:
- для четных
 :
: 
- для нечетных
 :
:  ,
,
где ![\chi = E[(\varepsilon-1)/2]-1,E[*]](/sites/default/files/tex_cache/940bc609b7ebfd337e5a79540a800a4e.png) - целая часть
- целая часть ![[*]](/sites/default/files/tex_cache/c082fefb827614c9ae634bb4dd891270.png) .
.
Приняв за четный последний столбец  -спецификации (4.13), комбинаторную схему порождения всех
-спецификации (4.13), комбинаторную схему порождения всех  -транспозиций, генерируемых оператором линейной свертки булевых векторов, можно представить:
-транспозиций, генерируемых оператором линейной свертки булевых векторов, можно представить:
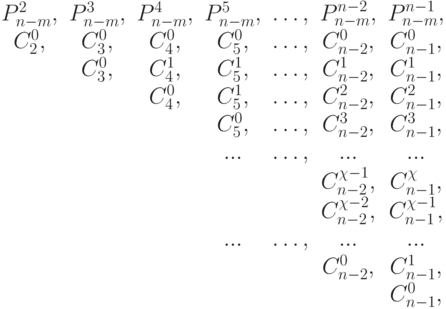 |
( 4.15) |
Здесь в 1-й строке указаны постоянные для каждого столбца множители  соответствующие мощностям подклассов образующих
соответствующие мощностям подклассов образующих  -транспозиций
-транспозиций  -спецификаций.
-спецификаций.
 |
Транспозиции типа 
|
 |
Транспозиции типа 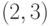
|
 |
Транспозиции типа 
|
|---|---|---|---|---|---|
 |
 |
 |
 |
 |
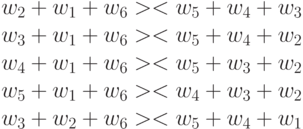 |
 |
 |
 |
 |
 |
|
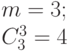 |
 |
 |
 |
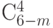 |
Транспозиции типа 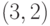
|
 |
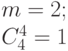 |
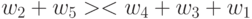 |
 |
 |
|
 |
Транспозиции типа 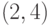
|
 |
 |
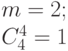 |
 |
 |
 |
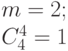 |
 |
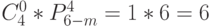 |
|
 |
 |
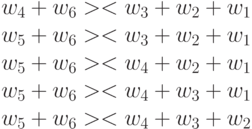 |
 |
Транспозиции типа 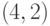
|
|
 |
 |
 |
 |
||
 |
 |
||||
Сумма элементов  столбца из (4.15) представляет собой мощность множества
столбца из (4.15) представляет собой мощность множества  -транспозиций, порожденных каждой образующей соответствующего типа:
-транспозиций, порожденных каждой образующей соответствующего типа:

Общее число  -транспозиций, генерируемых оператором линейной свертки булевых векторов при ограничении (4.10) на компоненты весового вектора:
-транспозиций, генерируемых оператором линейной свертки булевых векторов при ограничении (4.10) на компоненты весового вектора:
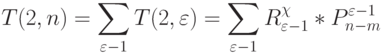 |
( 4.16) |
или
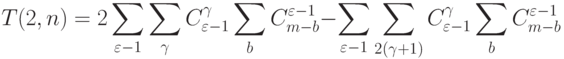
где  , а
, а  .
.
