Методы генерации признаков
11.5. Генерация признаков на основе нелинейных преобразований. Выделение текстуры изображений.
Пусть дано изображение или его часть (область). Задача состоит в генерации признаков, которые впоследствии будут использоваться при классификации.
Определение. Цифровое изображение (монохромное) есть результат
процесса дискретизации непрерывной функции 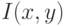 в виде двумерного массива
в виде двумерного массива  , где
, где  ,
,  . Значение функции
. Значение функции 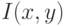 – интенсивность, число градаций
– интенсивность, число градаций  – глубина изображения.
– глубина изображения.
Определение. Генерацией признаков называется эффективное кодирование необходимой для классификации информации, содержащейся в оригинальных (исходных) данных.
11.5.1. Региональные признаки. Признаки для описания текстуры.
Дадим не точное определение текстуры.
Определение. Текстурой называется распределение оттенков серого цвета среди пикселов в регионе.
Рассмотрим основные типы характеристик:
- тонкие – грубые,
- гладкие – резкие (нерегулярные),
- однородные – неоднородные.
Отметим, что в основе подхода лежит гипотеза о том, что внутри региона значения интенсивностей описываются одинаково, т.е. одним и тем же распределением вероятностей.
Пусть интенсивность внутри региона есть случайная величина. Тогда, при условии, что внутри региона характеристики одинаковы, данная случайная величина внутри региона одинаково распределенная, чем обеспечивается свойство однородности в регионе.
Нашей целью является генерация признаков, которые как-то квантуют свойства фрагментов изображения (регионов).
Данные признаки появляются при анализе пространственных соотношений по распределению серых цветов.
11.5.1.1. Признаки, основанные на статистиках первого порядка.
Пусть  – интенсивность случайной величины, представляющая собой
значение (уровень интенсивности) серого цвета в регионе. Пусть также
– интенсивность случайной величины, представляющая собой
значение (уровень интенсивности) серого цвета в регионе. Пусть также  – вероятность, того что интенсивность в регионе равна
– вероятность, того что интенсивность в регионе равна  .
.
Определение. Гистограммой первого порядка называется величина 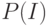 ,
равная отношению числа пикселов с уровнем интенсивности
,
равная отношению числа пикселов с уровнем интенсивности  к общему
числу пикселов в регионе и обозначается
к общему
числу пикселов в регионе и обозначается  .
.
Рассмотрим центральный момент:

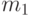 – среднее значение интенсивности – первый
момент, который в общем случае определяется из формулы:
– среднее значение интенсивности – первый
момент, который в общем случае определяется из формулы:

Среди центральных моментов наиболее часто используются
-
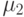 – дисперсия
– дисперсия  ,
, -
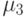 – ассиметрия,
– ассиметрия, -
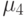 – эксцесс.
– эксцесс.
В качестве признаков, основанных на статистиках первого порядка, также может использоваться абсолютный момент:

![\def\I{\mathop{I}}
H=-E\left[\log_2 P(\I\limits^{.})\right]
=-\sum_{\I\limits^{.}=0}^{N_g-1}P(\I\limits^{.})\log_2(P(\I\limits^{.})),](/sites/default/files/tex_cache/072d06e154663bf7aefb15f90da0e462.png)
11.5.1.2. Признаки, основанные на статистиках второго порядка. Матрицы сочетаний.
Пусть  – относительное расстояние между пикселами,
– относительное расстояние между пикселами,  – ориентация.
Тогда можем ввести метрику следующим образом:
– ориентация.
Тогда можем ввести метрику следующим образом:
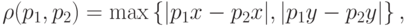
Рассмотрим соседство для четырех пикселей. Пусть  , т.е у нас
имеется горизонтальное, вертикальное, диагональное и антидиагональное
соседство.
, т.е у нас
имеется горизонтальное, вертикальное, диагональное и антидиагональное
соседство.
Обозначим через  совместную плоскость. Рассмотрим
совместную плоскость. Рассмотрим  .
.  – вероятность того, что точки, расположенная на горизонтали
– вероятность того, что точки, расположенная на горизонтали  имеют
интенсивности
имеют
интенсивности 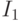 и
и  , равные отношению числа пар пикселов
с расстоянием
, равные отношению числа пар пикселов
с расстоянием  и значением
и значением 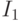 и
и  к общему
числу пикселов в регионе.
к общему
числу пикселов в регионе.
Аналогично считается 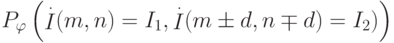 для
для  ;
;  для
для  ;
;  для
для  . Каждый такой
массив называют матрицей сочетаний или матрицей пространственной
зависимости.
. Каждый такой
массив называют матрицей сочетаний или матрицей пространственной
зависимости.
Рассмотрим конкретный пример матрицы  .
Пусть
.
Пусть 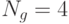 , т.е. уровни интенсивности изменяются от 0 до 3.
Пусть также матрица
, т.е. уровни интенсивности изменяются от 0 до 3.
Пусть также матрица  задана
следующим образом:
задана
следующим образом:

Т.к. просмотр происходит в обе стороны, то общее количество пар равно 24.
Рассмотрим  и
и 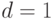 .
.  .
Очевидно, что матрица
.
Очевидно, что матрица  является симметрической.
является симметрической.

Для  и
и 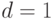 матрица
матрица  выглядит следующим образом:
выглядит следующим образом:

Существуют следующие основные виды признаков, основанные на статистиках второго порядка:
Угловой момент второго порядка:  – мера гладкости изображения. При малой вариации
– мера гладкости изображения. При малой вариации  ,
а при больших вариациях (например при увеличении) контраста
,
а при больших вариациях (например при увеличении) контраста  .
.
Контраст (по заданной паре):  – мера локальной дисперсии серого.
– мера локальной дисперсии серого.
Момент обратной разности:  .
Момент обратной разности имеет большое
значение для слабоконтрастных изображений.
.
Момент обратной разности имеет большое
значение для слабоконтрастных изображений.
Энтропия:  – мера равномерности. Энтропия связана с фиксированной
ориентацией и фиксированным расстоянием.
– мера равномерности. Энтропия связана с фиксированной
ориентацией и фиксированным расстоянием.

