Нейронные сети ассоциативной памяти
Для рассматриваемых сетей с ортогональным проектированием также возможно простое дообучение. На первый взгляд, это может показаться странным - если добавляемый эталон линейно независим от старых эталонов, то вообще говоря необходимо пересчитать матрицу Грамма и обратить ее. Однако симметричность матрицы Грамма позволяет не производить заново процедуру обращения всей матрицы. Действительно, обозначим через 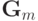 - матрицу Грамма для множества из
- матрицу Грамма для множества из  векторов
векторов 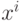 ; через
; через 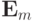 - единичную матрицу размерности
- единичную матрицу размерности 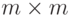 . При обращении матриц методом Гаусса используется следующая процедура:
. При обращении матриц методом Гаусса используется следующая процедура:
- Запишем матрицу размерности
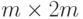 следующего вида:
следующего вида:  .
. - Используя операции сложения строк и умножения строки на ненулевое число преобразуем левую квадратную подматрицу к единичной. В результате получим
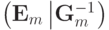 .
.
Пусть известна 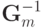 - обратная к матрице Грамма для множества из m векторов
- обратная к матрице Грамма для множества из m векторов 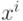 . Добавим к этому множеству вектор
. Добавим к этому множеству вектор  . Тогда матрица для обращения матрицы
. Тогда матрица для обращения матрицы  методом Гаусса будет иметь вид:
методом Гаусса будет иметь вид:
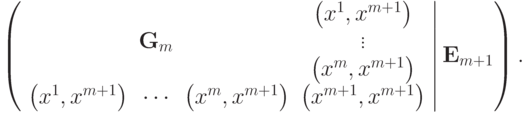
После приведения к единичной матрице главного минора ранга m получится следующая матрица:
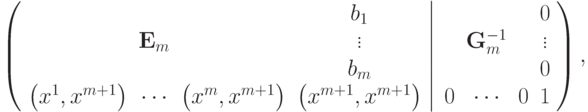
где 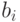 - неизвестные величины, полученные в ходе приведения главного минора к единичной матрице. Для завершения обращения матрицы
- неизвестные величины, полученные в ходе приведения главного минора к единичной матрице. Для завершения обращения матрицы  необходимо привести к нулевому виду первые m элементов последней строки и
необходимо привести к нулевому виду первые m элементов последней строки и 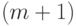 -о столбца. Для обращения в ноль i -о элемента последней строки необходимо умножить i -ю строку на
-о столбца. Для обращения в ноль i -о элемента последней строки необходимо умножить i -ю строку на 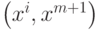 и вычесть из последней строки. После проведения этого преобразования получим
и вычесть из последней строки. После проведения этого преобразования получим
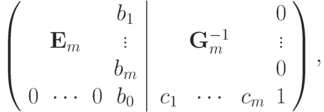
где
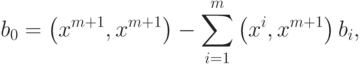
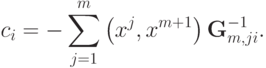
 только если новый эталон является линейной комбинацией первых m эталонов. Следовательно
только если новый эталон является линейной комбинацией первых m эталонов. Следовательно  . Для завершения обращения необходимо разделить последнюю строку на
. Для завершения обращения необходимо разделить последнюю строку на  и затем вычесть из всех предыдущих строк последнюю, умноженную на соответствующее номеру строки
и затем вычесть из всех предыдущих строк последнюю, умноженную на соответствующее номеру строки 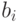 . В результате получим следующую матрицу
. В результате получим следующую матрицу
где 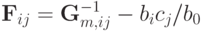 . Поскольку матрица, обратная к симметричной, всегда симметрична получаем
. Поскольку матрица, обратная к симметричной, всегда симметрична получаем  при всех i. Так как
при всех i. Так как  следовательно
следовательно 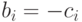 .
.
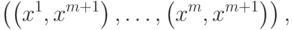
 - вектор
- вектор  . Используя эти обозначения можно записать
. Используя эти обозначения можно записать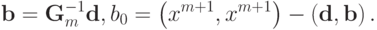
 записывается в виде
записывается в виде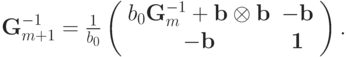
Таким образом, при добавлении нового эталона требуется произвести следующие операции:
- Вычислить вектор
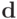 (
(  скалярных произведений -
скалярных произведений - 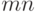 операций,
операций, 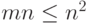 ).
). - Вычислить вектор
 (умножение вектора на матрицу -
(умножение вектора на матрицу - 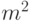 операций).
операций). - Вычислить
 (два скалярных произведения -
(два скалярных произведения -  операций).
операций). - Умножить матрицу на число и добавить тензорное произведение вектора
 на себя (
на себя (  операций).
операций). - Записать
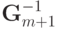 .
.
Таким образом, эта процедура требует  операций. Тогда как стандартная схема полного пересчета потребует:
операций. Тогда как стандартная схема полного пересчета потребует:
- Вычислить всю матрицу Грамма (
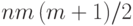 операций).
операций). - Методом Гаусса привести левую квадратную матрицу к единичному виду (
 операций).
операций). - Записать
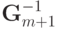 .
.
Всего 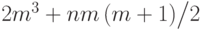 операций, что в
операций, что в 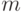 раз больше.
раз больше.
Используя ортогональную сеть (6), удалось добиться независимости способности сети к запоминанию и точному воспроизведению эталонов от степени скоррелированности эталонов. Так, например, ортогональная сеть смогла правильно воспроизвести все буквы латинского алфавита в написании, приведенном на рис. 8.1.
У сети (6) можно выделить два основных недостатка:
- Число линейно независимых эталонов должно быть меньше размерности системы
 .
. - Неинвариантностью - если два визуальных образа отличаются только своим положением в рамке, то в большинстве задач желательно объединять их в один эталон.
Оба этих недостатка можно устранить, изменив выбор весовых коэффициентов в (2).
