НОУ ИНТУИТ | Нейроинформатика. Лекция 6: Погрешности в нейронных сетях

Учитесь и получайте официальные документы БЕСПЛАТНО. Вы можете поддержать наш проект.

Регистрация Вход

Твой путь к знаниям!

Опубликован: 01.03.2007 | Доступ: свободный | Студентов: 1591 / 212 | Оценка: 4.58 / 4.39 | Длительность: 20:15:00

Тема: Искусственный интеллект и робототехника

Специальности: Программист

|

Вам нравится? Нравится 28 студентам

| Поделиться |

Поддержать курс

| Скачать электронную книгу

Метод обратного распространения точности для гарантированных интервальных оценок

Пусть нам заданы допустимые погрешности вычислений для выходных сигналов сети. Для каждого элемента решим задачу: определить допустимые погрешности на входах элемента по заданным максимально допустимым погрешностям на его выходе. Если эту задачу решить для каждого элемента сети, то можно оценить допустимые погрешности для всех сигналов, проходящих через сеть, переходя по сети от элемента к элементу в обратном направлении (от выходов сети к ее входам). Этот процесс мы назовем обратным распространением точности. В ходе него движение сигналов происходит от выходов ко входам, сигнал, проходящий по связи в обратном направлении, является допустимой погрешностью сигнала, проходящего по этой связи в прямом направлении.

Последним элементом стандартного нейрона является точка ветвления, поэтому начинаем рассмотрение метода обратного распространения точности именно с нее.

Точка ветвления имеет несколько выходов. Пусть для каждого ее выхода задана допустимая погрешность 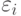$\varepsilon_i$ ( i - номер выхода). Для того, чтобы удовлетворить всем этим ограничениям погрешности, необходимо и достаточно, чтобы входной сигнал точки ветвления имел погрешность 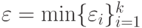$\varepsilon = \min \{\varepsilon_i \}_{i = 1}^k$ . Таким образом, при обратном распространении точности точка ветвления заменяется на двойственный элемент, выбирающий из поступающих сигналов 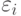$\varepsilon_i$ (т.е. погрешностей) минимальный.

Следующим элементом стандартного нейрона является нелинейный преобразователь. Пусть входной сигнал нелинейного преобразователя равен 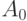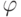A_0 , $\varphi$ - его функция активации, 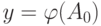$y = \varphi (A_0 )$ - выходной сигнал и 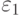$\varepsilon_1$ - допустимая погрешность выходного сигнала. 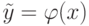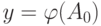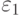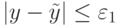Вычислим максимальную погрешность $\varepsilon$ входного сигнала нелинейного преобразователя, то есть найдем отрезок $[A_0 - \varepsilon ,A_0 + \varepsilon]$ такой, что для любого $x \in [A_0 - \varepsilon ,A_0 + \varepsilon ]$ $\tilde y = \varphi (x)$ отличается от $y = \varphi (A_0 )$ не более, чем на $\varepsilon_1$ : $|y - \tilde y| \le \varepsilon_1$ .

Ввиду непрерывности и дифференцируемости функции активации нелинейного преобразователя очевидно, что $\varepsilon \le \varepsilon_1 /\max |\varphi '(x)|$ , где

$x \in [\varphi^{-1}(y - \varepsilon_1 ),\varphi^{- 1}(y + \varepsilon_1 )].$

Пойдем традиционным путем, оценивая допустимую погрешность в линейном приближении: 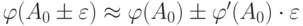$\varphi (A_0 \pm \varepsilon ) \approx \varphi (A_0 ) \pm \varphi '(A_0 ) \cdot \varepsilon$ . По условию

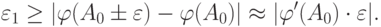
$\varepsilon_1 \ge |\varphi (A_0 \pm \varepsilon ) - \varphi (A_0 )| \approx |\varphi '(A_0 ) \cdot \varepsilon |.$

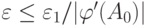Пользуясь этим неравенством, подберем $\varepsilon$ следующим образом: $\varepsilon \le \varepsilon_1 /|\varphi '(A_0 )|$ . В этом случае формула для вычисления допустимой погрешности более простая, но менее точная.

Получили погрешность, допустимую для входного сигнала нелинейного преобразователя, которая одновременно является допустимой погрешностью для выходного сигнала сумматора. Аналогично можем вычислить погрешность входного сигнала нелинейного преобразователя любого стандартного нейрона, если известна погрешность его выходного сигнала.

Двойственный к нелинейному преобразователю элемент - просто линейная связь! Ее вес равен 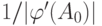$1/|\varphi '(A_0 )|$ для линейного приближения в формуле ошибки или 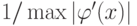$1/\max |\varphi '(x)|$ - в более общем случае (в последней формуле максимум берется по отрезку $x \in [\varphi^{- 1}(y - \varepsilon_1 ),\varphi^{- 1}(y + \varepsilon_1 )]$ - так что линейность здесь уже кажущаяся).

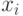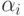Перейдем к следующему элементу стандартного нейрона - адаптивному сумматору с синапсами, являющимися его входами. Адаптивный сумматор - это сумматор, в котором входные сигналы x_i суммируются с весами $\alpha_i$ .

Каждый вход 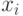x_i сумматора 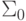$\Sigma_0$ имеет некоторую погрешность 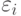$\varepsilon_i$ , которая вносит свой вклад в допустимую погрешность выходного сигнала сумматора. Эти погрешности могут иметь различные величины в зависимости от того, какой способ распределения допустимой погрешности выходного сигнала по входам сумматора мы выберем. Погрешности по входам сумматора могут распределяться равномерно, пропорционально и приоритетно.

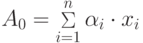Рассмотрим сначала равномерное распределение. Для этого полагаем, что на всех входах погрешности равны между собой $(\varepsilon_1 = \varepsilon_i , i = 2,...,n)$ . Пусть $A_0 = \mathop \Sigma \limits_{i = 1}^n \alpha_i \cdot x_i$ - выходной сигнал сумматора без погрешностей. 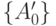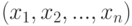Тогда $\{A'_0 \}$ - множество выходных сигналов сумматора, получающихся, когда вектор входных сигналов сумматора пробегает вершины - мерного куба с центром в точке (x_1 ,x_2 ,...,x_n ) и ребром длины

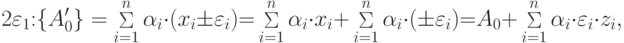
$2\varepsilon_1 {\rm{: }}\{A'_0 \} = \mathop \Sigma \limits_{i = 1}^n \alpha_i \cdot (x_i \pm \varepsilon_i ){\rm{ = }}\mathop \Sigma \limits_{i = 1}^n \alpha_i \cdot x_i {\rm{+ }}\mathop \Sigma \limits_{i = 1}^n \alpha_i \cdot ( \pm \varepsilon_i ){\rm{ = }}A_0 {\rm{+ }}\mathop \Sigma \limits_{i = 1}^n \alpha_i \cdot \varepsilon_i \cdot z_i ,$

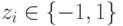где $z_i \in \{- 1,1\}$ . Нам требуется, чтобы все множество значений 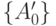$\{A'_0 \}$ попало в интервал $[A_0 - \varepsilon ,A_0 + \varepsilon ]$ . Для этого необходимо, чтобы

$\max |\mathop \Sigma \limits_{i = 1}^n \alpha_i \cdot \varepsilon_i \cdot z_i |{\rm{ = }}\mathop \Sigma \limits_{i = 1}^n |\alpha_i | \cdot \varepsilon_i \le \varepsilon ,$

где максимум берется по всем z_i

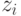. Из этого неравенства и сделанного выше предположения о 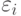$\varepsilon_i$ получаем требуемую оценку для равномерного распределения 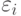$\varepsilon_i$ по входам сумматора: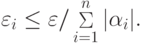

$\varepsilon_i \le \varepsilon /\mathop \Sigma \limits_{i = 1}^n |\alpha_i | .$

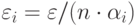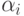При пропорциональном распределении погрешностей допустимая погрешность выходного сигнала сумматора делится сначала на число входов, а затем для каждого входа делится на соответствующий вес синапса. То есть погрешности распределяются пропорционально весам соответствующих синапсов. Формула расчета допустимой погрешности для каждого входа сумматора имеет вид: $\varepsilon_i = \varepsilon /(n \cdot \alpha_i )$ , где $\varepsilon$ - допустимая погрешность выходного сигнала сумматора, - число входов сумматора, $\alpha_i$ - веса синапсов соответствующих входов сумматора.

При приоритетном распределении погрешностей сначала назначаются погрешности для тех входов, которые наиболее значимы по какому-либо признаку, а затем оставшуюся часть допустимой погрешности выходного сигнала сумматора распределяют между оставшимися входами равномерно или пропорционально.

Аналогично можно вычислить допустимые погрешности для входных сигналов сумматора любого стандартного нейрона, если известны погрешности для выходного сигнала сумматора.

Дальше >>

Авторизоваться

Нейроинформатика

Погрешности в нейронных сетях

Метод обратного распространения точности для гарантированных интервальных оценок

Вопросы и ответы