Нейронные сети и ...
Адаптация функций принадлежности
В лекции, посвященной извлечению знаний из обученных нейронных сетей, мы познакомились с методами интерпретации отображения сетью
входной информации в выходную с помощью правил типа неравенств, правил m-of-n и других. В теории нечетких множеств соответствующие
нечеткие правила уже изначально имеют наглядный смысл. Например,  : если разрыв между бедными и богатыми высок, то уровень преступности повышен.
: если разрыв между бедными и богатыми высок, то уровень преступности повышен.
Конечно заманчиво иметь возможность получения не только качественного, но и количественного правила, связывающего уровень разрыва в доходах с преступностью. Мы знаем, что нейронные сети типа персептрона являются универсальными аппроксиматорами и могут реализовать любое количественное отображение. Хорошо бы поэтому построить нейронную сеть так, чтобы она, во-первых, воспроизводила указанное нечеткое качественное правило (чтобы изначально знать интерпретацию работы сети) и, во-вторых, давала хорошие количественные предсказания для соответствующего параметра (уровня преступности). Очевидно, что добиться этого можно подбором соответствующих функций принадлежности. А именно, задача состоит в том, чтобы так определить понятия "высокий разрыв в доходах" и "повышенный уровень преступности", чтобы выполнялись и качественные и количественные соотношения. Нужно, чтобы и сами эти определения не оказалось дикими - иначе придется усомниться в используемом нами нечетком правиле. Если такая задача успешно решается, то это означает успешный симбиоз теории нечетких множеств и нейронных сетей, в которых "играют" наглядность первых и универсальность последних.
Рассмотрим соответствующую методику на следующем примере.Обозначим  - курс доллара США ($) по отношению к немецкой марке (DM);
- курс доллара США ($) по отношению к немецкой марке (DM);  - курс доллара США ($) по отношению к шведской кроне (SK);
- курс доллара США ($) по отношению к шведской кроне (SK); 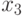 - курс доллара США ($) по отношению к финской марке (FM);
Предположим, что мы имеем три нечетких правила
- курс доллара США ($) по отношению к финской марке (FM);
Предположим, что мы имеем три нечетких правила
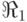 :если $ слаб по отношению к DM и слаб по отношению к SK и слаб по отношению к FM,
то величина портфеля очень высока
:если $ слаб по отношению к DM и слаб по отношению к SK и слаб по отношению к FM,
то величина портфеля очень высока
 : если $ силен по отношению к DM и силен по отношению к SK и слаб по отношению к FM,
то величина портфеля высока
: если $ силен по отношению к DM и силен по отношению к SK и слаб по отношению к FM,
то величина портфеля высока
 : если $ силен по отношению к DM и силен по отношению к SK и силен по отношению к FM,
то величина портфеля мала
: если $ силен по отношению к DM и силен по отношению к SK и силен по отношению к FM,
то величина портфеля мала
Формально, эти правила можно записать следующим образом 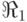 : если
: если  есть
есть 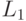 и
и  есть
есть 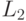 и
и 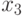 есть
есть 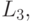 то PV есть VB
то PV есть VB  : если
: если  есть
есть 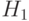 и
и  есть
есть 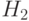 и
и 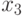 есть
есть 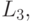 то PV есть B
то PV есть B  : если
: если  есть
есть 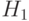 и
и  есть
есть 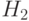 и
и 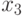 есть
есть 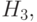 то PV есть S
Для всех нечетких правил
то PV есть S
Для всех нечетких правил 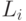 и
и 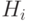 используем сигмоидные функции принадлежности
используем сигмоидные функции принадлежности
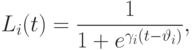
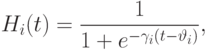
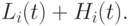
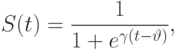
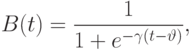
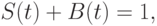
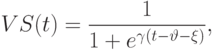
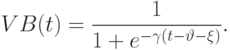
Предположим, что точные количественные значения курса доллара по отношению к немецкой марке, шведской кроне и финской марке равны 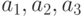 ,
соответственно. Поскольку любые значения этих курсов являются в какой-то мере слабыми и в какой-то мере сильными (а соответствующие
меры определяются функциями принадлежности), то все три правила вступают в игру. В этом случае можно определить уровень активации
каждого из них:
,
соответственно. Поскольку любые значения этих курсов являются в какой-то мере слабыми и в какой-то мере сильными (а соответствующие
меры определяются функциями принадлежности), то все три правила вступают в игру. В этом случае можно определить уровень активации
каждого из них:
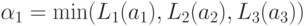
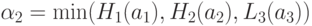
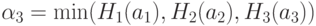
Теперь можно вычислить и количественные оценки величины портфеля, даваемые каждым из наших правил,
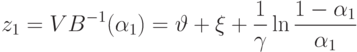
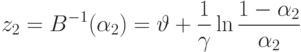
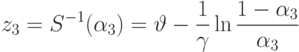
Оценка величины портфеля получается усреднением вышеприведенных оценок по уровням активации каждого из правил
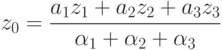
Ниже на рисунке приведена архитектура нейронной сети, эквивалентной описанной выше нечеткой системе ( рисунок 11.4).
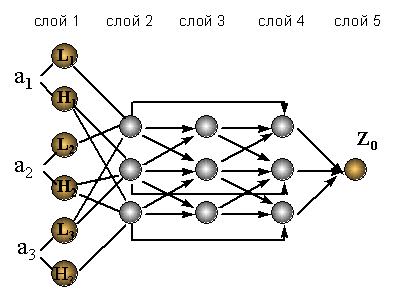
Рис. 11.4. Нейронная сеть (нечеткий персептрон), входами которой являются лингвистические переменные, выходом - четкое значение величины портфеля. Скрытые слои в нечетком персептроне называются слоями правил
Значения выходов в узлах первого слоя отражают степень соответствия входных значений лингвистическим переменным, связанными
с этими узлами. Элементы второго слоя вычисляют значения уровней активации соответствующих нечетких правил. Выходные значения нейронов
третьего слоя соответствуют нормированным значениям этих уровней активации 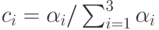 Выходные значения нейронов четвертого слоя вычисляются как произведения нормированных значений уровней активации правил на значения величины портфеля, соответствующего данной их
(ненормированной)активации.
Выходные значения нейронов четвертого слоя вычисляются как произведения нормированных значений уровней активации правил на значения величины портфеля, соответствующего данной их
(ненормированной)активации.
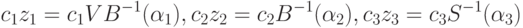
Наконец, единственный выходной нейрон (слой 5) просто суммирует воздействия нейронов предыдущего слоя.
Если мы имеем набор обучающих пар, содержащих точные значения курсов обмена 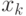 и точные значения величины портфеля:
и точные значения величины портфеля: 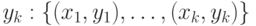 , то
определив ошибку сети для k-й обучающей пары обычным образом, как
, то
определив ошибку сети для k-й обучающей пары обычным образом, как 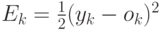 (
(  - реальное значение состояния выходного нейрона), можно
использовать метод градиентного спуска для коррекции значений параметров, управляющих формой функции принадлежности лингвистической
переменной "величина портфеля":
- реальное значение состояния выходного нейрона), можно
использовать метод градиентного спуска для коррекции значений параметров, управляющих формой функции принадлежности лингвистической
переменной "величина портфеля":
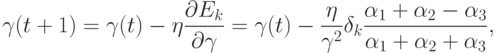
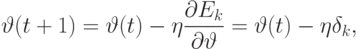
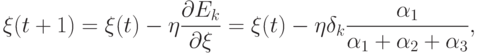
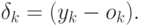
Аналогичным образом выводятся уравнения коррекции для параметров, управляющих формой функций принадлежности нечетких понятий
слабый 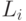 и сильный
и сильный 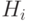 курс доллара:
курс доллара: 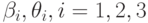 . Легко заметить, что особенность описанного нами совместного использования нейросетевого и
нечеткого подходов заключается в том, что адаптируются не величины связей между нейронами, а формы нелинейного преобразования,
осуществляемого нейронами (формы функции принадлежности). С нейрокомпьютерной точки зрения достоинства нечетких моделей как раз
и связаны с нелинейностью функции принадлежности. Фиксирование и изначальное задание архитектуры сети позволяет интерпретировать
ее решения. И что особенно важно, описанный подход по сути позволяет инкорпорировать априорные знания в структуру нейронной сети.
. Легко заметить, что особенность описанного нами совместного использования нейросетевого и
нечеткого подходов заключается в том, что адаптируются не величины связей между нейронами, а формы нелинейного преобразования,
осуществляемого нейронами (формы функции принадлежности). С нейрокомпьютерной точки зрения достоинства нечетких моделей как раз
и связаны с нелинейностью функции принадлежности. Фиксирование и изначальное задание архитектуры сети позволяет интерпретировать
ее решения. И что особенно важно, описанный подход по сути позволяет инкорпорировать априорные знания в структуру нейронной сети.
