Нейронные сети и ...
Нечеткие нейроны
Преобразование, осуществляемое типичным нейроном с двумя входами, имеет вид  , где
, где 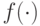 -сигмоидная функция. Для того, чтобы обобщить его, нужно представить себе, что вес нейрона не обязательно должен умножаться на значение
соответственного входа, а здесь может быть применена какая-либо другая операция. Далее, суммирование воздействий также может быть
заменено неким другим действием. Наконец, вместо сигмоидной функции потенциал нейрона может быть преобразован каким-либо новым способом.
В нечеткой логике операция умножения заменяется для булевых переменных операцией И, а для числовых - операцией взятия минимума (min).
Операция суммирования заменяется соответственно операциями ИЛИ и взятием максимума (max).
-сигмоидная функция. Для того, чтобы обобщить его, нужно представить себе, что вес нейрона не обязательно должен умножаться на значение
соответственного входа, а здесь может быть применена какая-либо другая операция. Далее, суммирование воздействий также может быть
заменено неким другим действием. Наконец, вместо сигмоидной функции потенциал нейрона может быть преобразован каким-либо новым способом.
В нечеткой логике операция умножения заменяется для булевых переменных операцией И, а для числовых - операцией взятия минимума (min).
Операция суммирования заменяется соответственно операциями ИЛИ и взятием максимума (max).
Если осуществить соответствующие замены в преобразовании, осуществляемом знакомым нам нейроном, и положить в нем 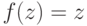 (линейный
выход), то мы получим так называемый нечеткий ИЛИ-нейрон:
(линейный
выход), то мы получим так называемый нечеткий ИЛИ-нейрон:
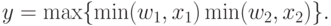
Для нечетких нейронов полагается, что значения входов и весов заключены в интервале [0, 1], поэтому и выход нейрона ИЛИ будет принадлежать этому же интервалу.
Используя противоположную подстановку (умножение max), (сложение min ) получим преобразование, характерное для нечеткого И-нейрона:
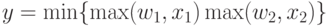
Извлечение правил if-then
В лекции, посвященной извлечению знаний, мы уже познакомились с нейросетевыми методами извлечения правил из данных. Настало время узнать, как можно извлечь с их помощью нечеткие правила.
Рассмотрим набор нечетких правил
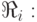
 есть
есть 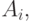 то
то  есть
есть 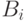 ,
, 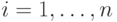
Каждое из них может интерпретироваться как обучающая пара для многослойного персептрона. При этом, условие (x есть  ) определяет
значение входа, а следствие (y есть
) определяет
значение входа, а следствие (y есть 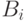 ) - значение выхода сети. Полное обучающее множество имеет вид
) - значение выхода сети. Полное обучающее множество имеет вид 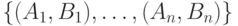 . Заметим, что каждому
лингвистическому значению
. Заметим, что каждому
лингвистическому значению 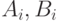 соответствует своя функция принадлежности, так что каждое нечеткое правило определяет связь двух
функций.
соответствует своя функция принадлежности, так что каждое нечеткое правило определяет связь двух
функций.
Если же правила имеют более сложный вид, типа "два входа - один выход":
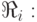
 есть
есть  и
и  есть
есть 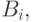 то
то  есть
есть 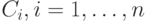 то обучающая выборка принимает форму
то обучающая выборка принимает форму 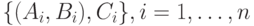 ,
Существует два основных подхода к реализации нечетких правил типа if-then с помощью многослойных персептронов.
,
Существует два основных подхода к реализации нечетких правил типа if-then с помощью многослойных персептронов.В методе Умано и Изавы нечеткое множество представляется конечным числом значений совместимости. Пусть 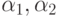 включает носители
всех
включает носители
всех  , входящих в обучающую выборку а также носители всех
, входящих в обучающую выборку а также носители всех 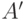 , которые могут быть входами в сети. Предположим также, что
, которые могут быть входами в сети. Предположим также, что ![[\beta_1\beta_2]](/sites/default/files/tex_cache/4a95b81900ef96dce950ace2c0051f8a.png) включает носители всех
включает носители всех  , входящих в обучающую выборку, а также носители всех
, входящих в обучающую выборку, а также носители всех  , которые могут быть входами в сети. Положим
, которые могут быть входами в сети. Положим
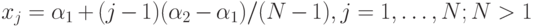
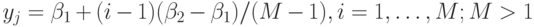
Дискретный аналог обучающего множества правил (заменяющее функциональное) имеет вид:
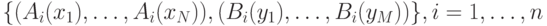
Если теперь ввести обозначения 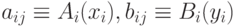 , то можно представить нечеткую нейронную сеть с
, то можно представить нечеткую нейронную сеть с  входными и
входными и  выходными нейронами (
рисунок 11.3).
выходными нейронами (
рисунок 11.3).
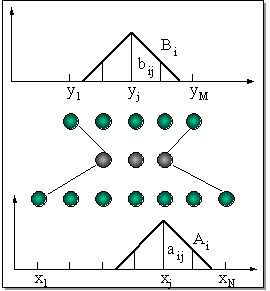
Рис. 11.3. Нечеткая нейронная сеть и треугольные функции принадлежности входных и выходных переменных
Пример 1. Предположим, что обучающая выборка включает три правила: 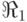 : Если город мал, то доход от продажи бриллиантов отрицателен,
: Если город мал, то доход от продажи бриллиантов отрицателен,  : Если город средний, то доход от продажи бриллиантов близок к нулю,
: Если город средний, то доход от продажи бриллиантов близок к нулю,  : Если город велик, то доход от продажи бриллиантов положителен.
: Если город велик, то доход от продажи бриллиантов положителен.
Функции принадлежности определим как
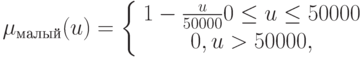
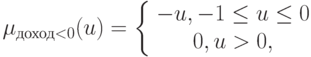
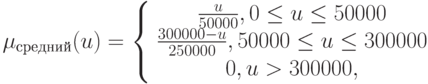
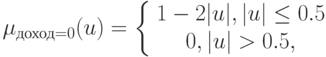
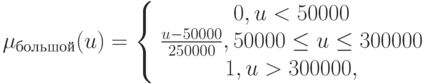
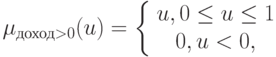
Тогда обучающая выборка принимает форму {(малый, отрицательный), (средний, близок к нулю), (большой, положительный)}
Если носитель множества входов [0, 10 000 000], то для покрытия множества населения городов равномерной сеткой, захватывающей
и малые города, понадобится несколько сот точек. Поэтому, ограничимся городами с населением 1 000 000 человек. Тогда можно выбрать 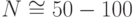 .
Носитель множества выходов [-1,1] может быть описан набором из
.
Носитель множества выходов [-1,1] может быть описан набором из 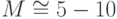 . Таким образом, в рассматриваемом случае сеть будет иметь умеренные
размеры (например 50 - ... - 5) и 3 пары в обучающем наборе.
. Таким образом, в рассматриваемом случае сеть будет иметь умеренные
размеры (например 50 - ... - 5) и 3 пары в обучающем наборе.
В методе Уехары и Фуджицы вместо разбиения равномерной сеткой области, покрывающей носители всех функций принадлежности, равномерно разбивается область изменения этих функций [0,1]. Здесь видна явная аналогия с переходом от интегрирования по Риману к интегралу Лебега. Остальные действия аналогичны уже описанным.
